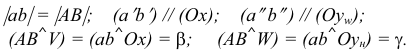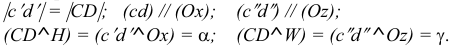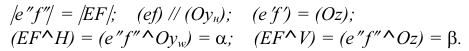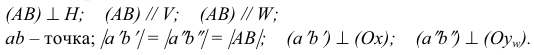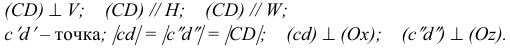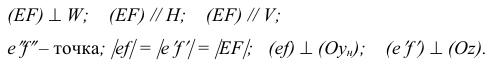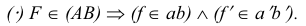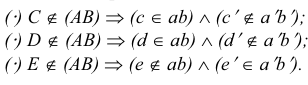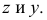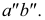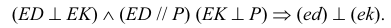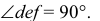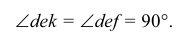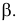Что значит точки совпадают

Точка совпадения

Резюме

Понятие точки совпадения

Рамка

В данный момент (отмечено t ) точка M находится в геометрической точке P пространства.

Определение

Характеристики

Используя совпадающую точку

Скоростной состав

Закон скоростной композиции записан:

v → в знак равно v → р + v → е <\ displaystyle <\ vec > _ <\ mathrm > = <\ vec > _ <\ mathrm > + <\ vec > _ <\ mathrm > >

Состав ускорений

Мы также определяем:

Формула для состава ускорений тогда определяется следующим образом:

в → в знак равно в → р + в → е + в → против <\ displaystyle <\ vec > _ <\ mathrm > = <\ vec > _ <\ mathrm > + <\ vec > _ <\ mathrm > + <\ vec > _ <\ mathrm >>

Примеры

Движение в машине

Тогда движение совпадающей точки представляет собой равномерное прямолинейное движение. Так:

Движение на карусели

Тогда движение совпадающей точки представляет собой равномерное круговое движение радиуса r. В полярной системе координат :

Использование в твердотельной кинематике

Мы можем привязать систему координат к каждому твердому телу. Рассмотрим две части с названиями 1 и 2. Итак, мы рассматриваем точку M части 1; это материальный момент. Обозначение «M ∈ 1» обозначает соответствующую геометрическую точку в системе отсчета 1 (отмечено Q выше). Обозначение «M ∈ 2» обозначает геометрическую точку в системе отсчета 2, совпадает с материальной точкой M (отмеченной выше P). Так,

Таким образом, мы можем рассматривать вектор скорости центра ступицы детали, хотя там нет материала. Если A является центром шарнирного соединения между осью 1 и подшипником 2,

V → ( В ∈ 2 / 1 ) знак равно 0 → <\ Displaystyle <\ vec <\ mathrm >> (\ mathrm \ in 2/1) = <\ vec <0>>>

и вывести из рамы машины, помеченной 0:

V → ( В ∈ 1 / 0 ) знак равно V → ( В ∈ 2 / 0 ) <\ displaystyle <\ vec <\ mathrm >> (\ mathrm \ in 1/0) = <\ vec <\ mathrm >> (\ mathrm \ in 2/0) > .

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Начертательная геометрия: конспект лекций

Данное учебное пособие представляет собой курс лекций и предназначено для студентов, сдающих экзамен по специальности «Начертательная геометрия». Подготовлено с учетом требований Министерства образования РФ.

Оглавление

Приведённый ознакомительный фрагмент книги Начертательная геометрия: конспект лекций предоставлен нашим книжным партнёром — компанией ЛитРес.

1. Проекции точки на две плоскости проекций

Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.

Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.

Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…

Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…

При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.

Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аа_х, а фронтальную плоскость — по прямой а́а_х. Прямые аах и а́а_х являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.

При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аа_х и а́а_х не нарушится.

Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.

Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.

Рассмотрим прямоугольник Aaa_ха́ (рис. 5), для которого справедливы следующие утверждения:

1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.

2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.

Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.

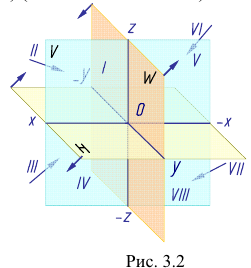
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).

Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.

При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.

На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.

При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.

Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.

Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.

В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.

В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.

Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.

Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.

Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.

2. Отсутствие оси проекций

Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.

Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.

При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.

Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.

3. Проекции точки на три плоскости проекций

Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.

Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.

В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.

Источник

Что значит точки совпадают

Рассмотрим три основных варианта взаимного расположения точек, в зависимости от соотношения координат определяющих их положение в пространстве:

1. Рассмотрим точки А и В (рис.13), все три координаты которых отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций:

— Y_А>Y_В. Тогда точка А расположена дальше от плоскости П₂ и ближе к наблюдателю, чем точка В;

— Z_А>Z_В. Тогда точка А расположена дальше от плоскости П₁ и ближе к наблюдателю, чем точка В;

Рисунок 13. Взаимное расположение точек

2. На рисунке 14 представлены точки А, В, С, D , у которых одна из координат совпадает, а две другие отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций следующим образом:

– Z_А=Z_В=Z_С, то точки А, В и С равноудалены от плоскости П₁ и их фронтальные и профильные проекции расположены, соответственно, на прямых А₂ В₂//x₁₂ и А ₃С ₃ // y. Геометрическим местом таких точек служит плоскость, параллельная П₁ ;

3. Если у точек равны две одноименные координаты, то они называются конкурирующими . Конкурирующие точки расположены на одной проецирующей прямой. На рис. 14. даны три пары таких точек, у которых:

Рисунок 14. Конкурирующие точки

Соответствующие проекции конкурирующих точек совпадают.

При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.

Источник

Точка и прямая в начертательной геометрии с примерами

Содержание:

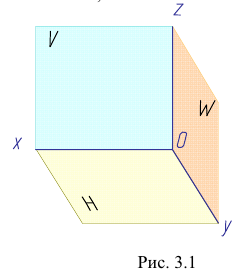
Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.

Введем в систему плоскостей

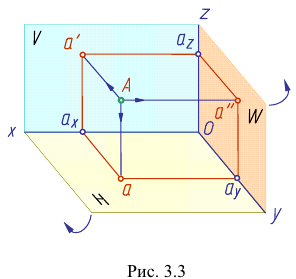
Чертеж точки

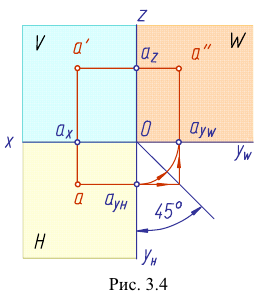
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).

Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, 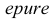— чертеж, проект).

На эпюре мы не можем показать пространственную картину рас­положения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.

Таким образом, на комплексном чертеже трех ортогональных проекций точки

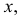
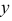
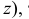
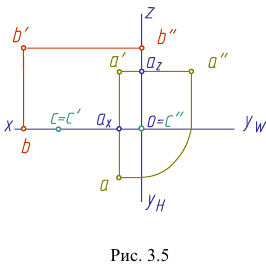
Положение точки в пространстве задается при помощи трех се координат (абсциссы ординаты и аппликаты то есть трех чисел, вы­ражающих расстояние от этой точки до координатных плоскостей проекций. Запись координат точки производят в такой форме: А (х, у, z). Положение точки на плоскости определяют две координаты: а(х,у); a'(x,z); a»(y,z).

По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она ле­жит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.

Взаимное положение двух точек. Условия видимости на чер­теже

Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?

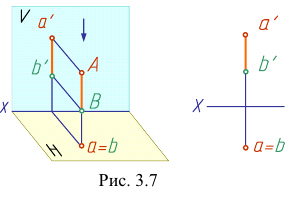
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.

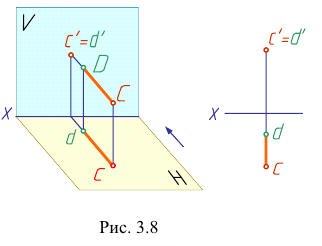
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).

Из двух профильно-конкурирующих точек на профильной плоскости проекций бу­дет видима та точка, которая расположена левее.

Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).

Чертёж отрезка прямой. Прямые частного положения

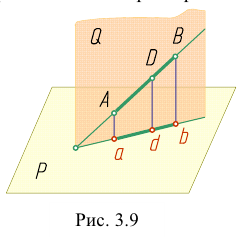
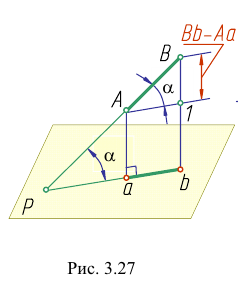
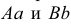
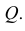
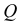
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые образуют проецирующую плоскость Линия пере­сечения плоскостей и Р проходит через проекции а и b точек А и В на плоскости ­ проекций Р. Эта линия и является единственной проекцией прямой АВ на плоскости проекций Р.

Относительно плоскостей проекции прямая может занимать различные положения:

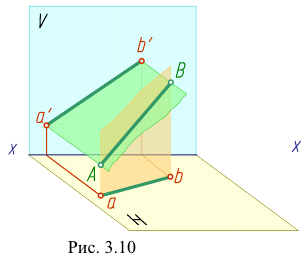
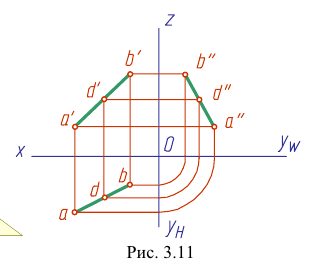
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).

Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.

Различают три вида таких прямых.

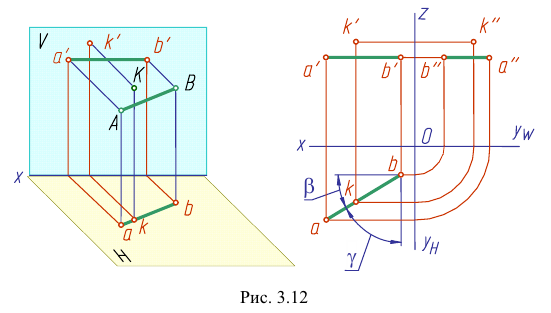
Прямая АВ параллельна плоскости Н

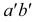
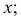
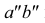
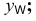
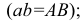
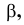
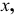
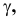
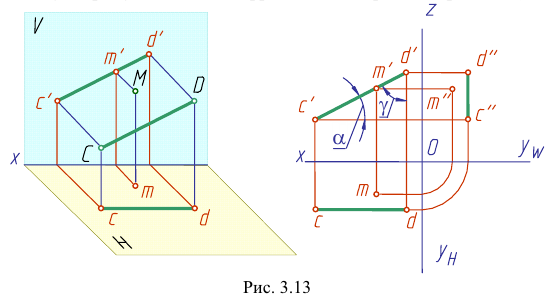
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой параллельна оси профильная проекция параллельна оси длина горизонтальной проекции отрезка равна длине самого отрезка угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к фронтальной плоскости проекций; угол образованный горизонтальной проекцией и осью проекции равен углу наклона прямой к профильной плоскости проекций:

Прямая CD параллельна плоскости V

Такую прямую называют «фронтальной прямой» (рис. 3.13).

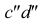
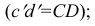
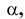
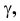
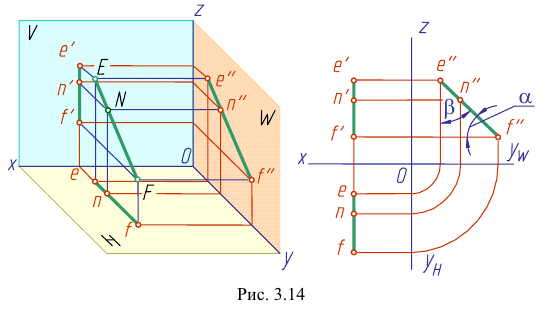
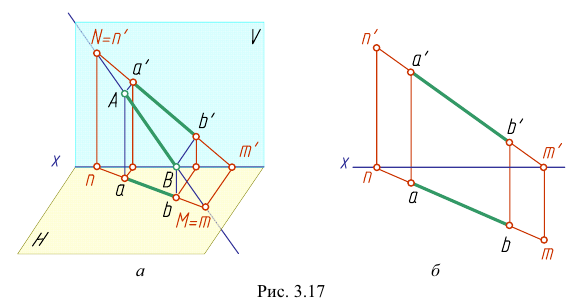
Горизонтальная проекция прямой cd параллельна оси х; профиль­ная проекция параллельна оси z; длина фронтальной проекции отрезка равна длине самого отрезка угол образованный фронтальной проекцией и осью проекций х, равен углу наклона прямой к горизонтальной плоскости проекций; угол образованный фронталь­ной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций:

Прямая EF параллельна плоскости IF

Такая прямая носит название «профильная прямая» (рис. 3.14).

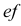
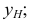
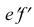
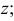
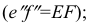
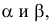
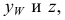
Горизонтальная проекция прямой параллельна оси фронтальная проекция параллельна оси длина профильной проекции отрезка равна длине самого отрезка углы образованные профильной проекцией с осями равны углам наклона прямой к горизонтальной и фронтальной плоскостям проекций соответственно:

Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту­ же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.

На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.

Прямая АВ перпендикулярна плоскости Н

Прямая CD перпендикулярна плоскости V

Прямая EF перпендикулярна плоскости W

Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций

Взаимное положение точки и прямой

Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.

Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.

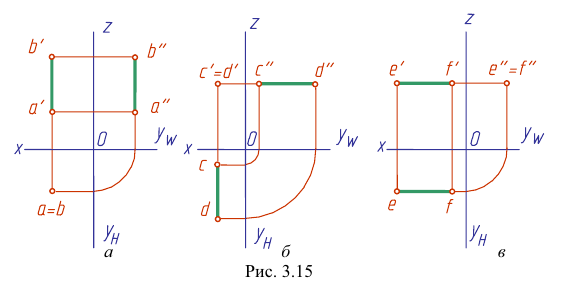
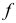
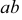
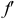
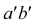
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция точки принадлежит горизонтальной проекции прямой, а фронтальная проекция точки принадлежит фронтальной проекции пря­мой:

Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.

Следы прямой

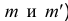
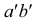
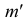
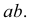
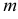
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки , надо продолжить фронтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции Точка — горизонтальная проекция горизонтального следа.

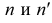
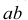
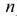
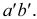
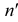
Для построения проекций фронтального следа (точек ) необ­ходимо продолжить горизонтальную проекцию прямой до пересечения с осью х (точка ). Затем через нес провести перпендикуляр к оси х до пересечения с продолжением фронтальной проекции Точка — фронтальная проекция фронтального следа. Построение проекций следов прямой показано на рис. 3.17, б.

Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях

Взаимное положение двух прямых

Прямые в пространстве могут занимать различные взаимные поло­жения:

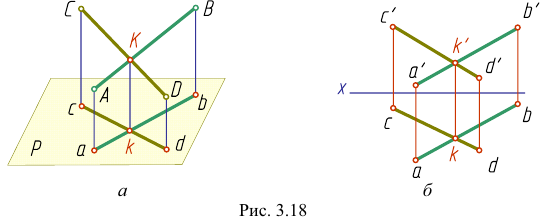
Пересекающиеся прямые

Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.

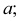
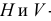
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, их чертеж в системе плоскостей -на рис. 3.18, б.

Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.

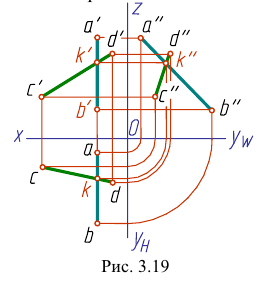
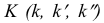
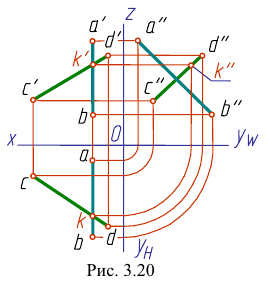
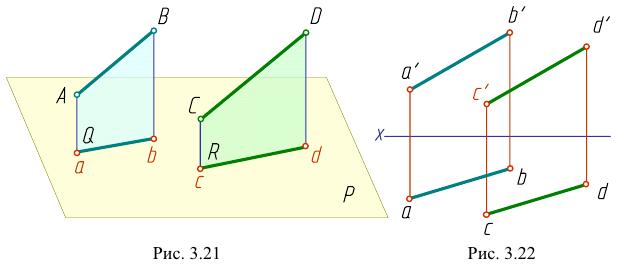
На рис. 3.19 все проекции точки одновременно принадлежат проекциям прямой АВ и прямой CD. Это значит, что прямые АВ и CD пересекаются.

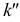
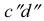
На рис. 3.20 профильная проекция точки К принадлежит профильной проекции и не принадлежит профильной проекции

Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.

Параллельные прямые

О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.

При этом нужно учитывать некоторые условия.

Для прямых общего положения:

Если одноименные проекции прямых общего положения парал­лельны в системе двух любых плоскостей проекций, то прямые парал­ лельны (рис. 3.22).

Для прямых частного положения:

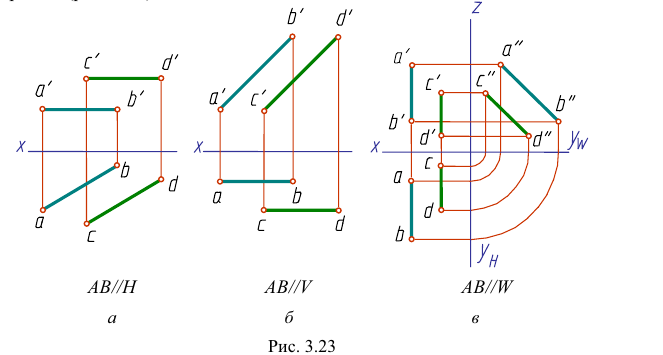
Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).

Скрещивающиеся прямые

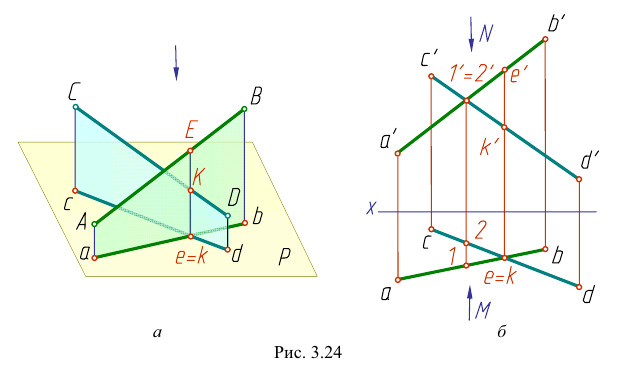
Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.

Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 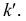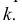3.24, б) фронтальная проекция е’ расположена выше фронтальной проекции При взгляде сверху по стрелке N при проецировании на плоскость Н точка е закрывает точку Прямая АВ проходит над прямой CD.

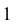
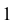
На плоскости V совпадают фронтальные проекции 1′ и 2′ точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка прямой АВ находится ближе к наблюдателю, и при проецировании на плоскость V точка прямой АВ закрывает точку 2 прямой CD. Прямая АВ расположена ближе к наблюдателю. Рассмотренные точки являются конкурирующими, так как они лежат на одной линии связи, но на разных прямых.

Проецирование плоских углов

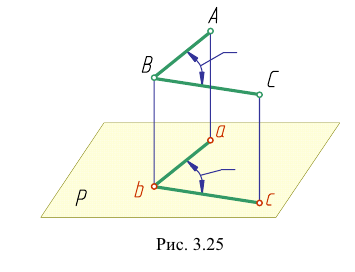
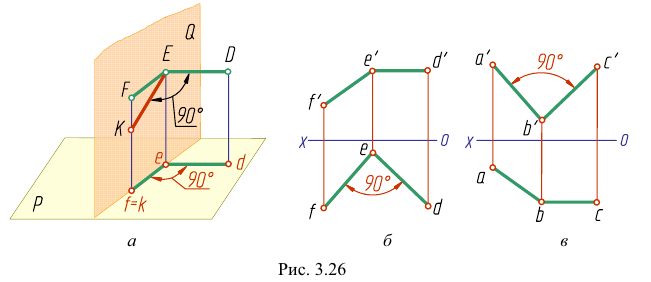
Любой линейный угол образуется двумя пересекающимися пря­мыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол 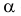спроецировался на нее без изменений.

Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого уг­ла.

Доказательство. Пусть угол 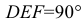и расположен так, что обе его стороны параллельны плоскости Р(рис. 3.26, а). Тогда, как и всякая фигура, лежащая в плоскости, параллельной Р, данный угол спроецируется на Р без искажения, то есть его проекция

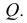
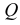
Через прямые EF и Ее проведем дополнительную плоскость Плоскость перпендикулярна плоскости Р.

Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.

Вторая сторона его ЕК наклонна к плоскости Р.

Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).

Определение истинной величины отрезка прямой

Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.

В этом случае используют способ построения прямоугольного треугольника.

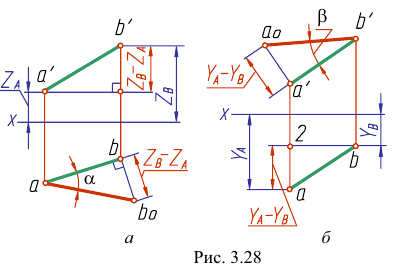
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 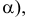если известны две проекции отрезка (рис. 3.28, а).

На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник