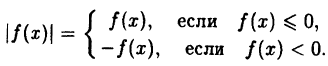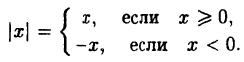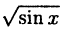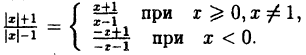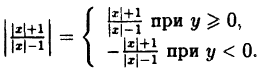Что значит сжать график
Преобразования графиков функций с примерами решения и образцами выполнения
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Параллельный перенос графиков
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b 0 — вниз, если b 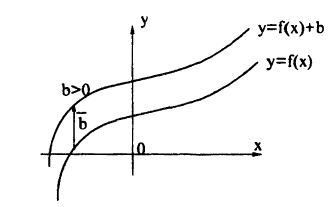
Пример:
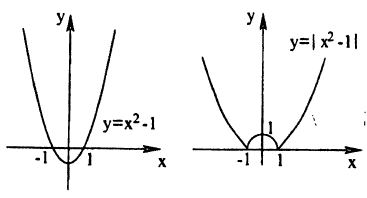
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
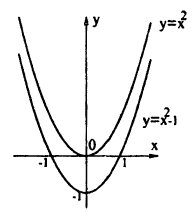
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а 0 — вправо, если α 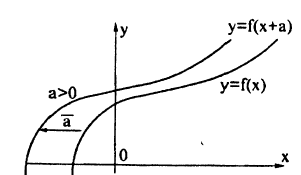
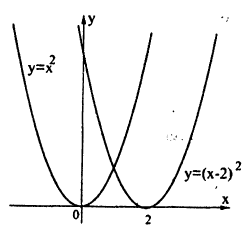
Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 0 можно исправить значения по оси Оу, умножив их на k. При k 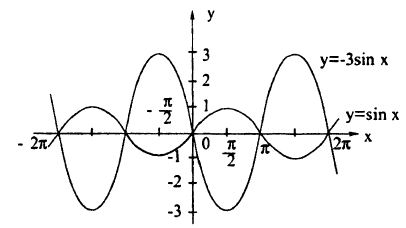
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 0 можно исправить значения по оси Ох, поделив их на k. При k 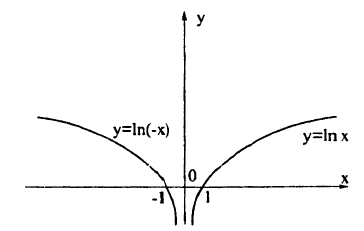
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
Пример:
Написать последовательность преобразований и построить график функции у = 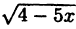
Решение:
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 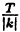
Построение графиков с модулями
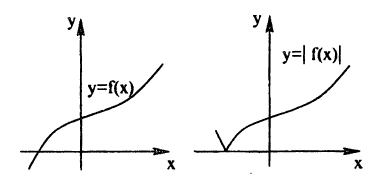
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
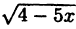
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
Действительно, по определению модуля действительного числа имеем:
(5.2)
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х 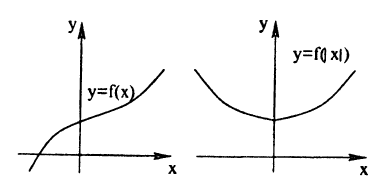
Пример:
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х 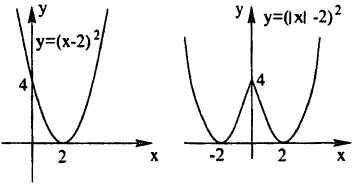
Кроме того, так как √u > и при 0 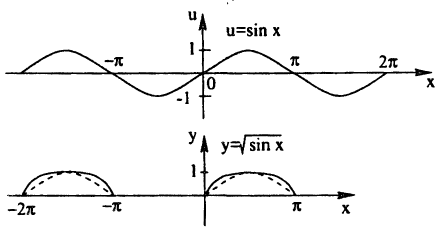
Построение графиков функций с примерами
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+ 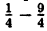
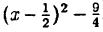
1) y =x²
2) у =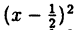
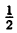
3) у = 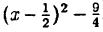
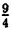
Пример:
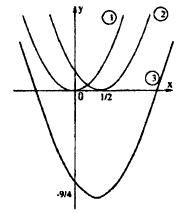
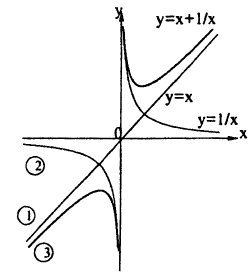
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
Пример:
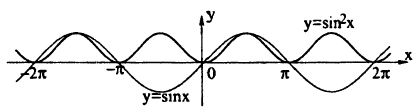
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
Постройте график функции в полярной системе координат: r = 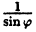
Решение:
Вычислим значения г для некоторых значений 
 | 0 | 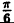 | 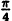 | 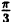 | 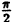 |
| r | ∞ | 2 | 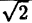 | 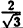 | ∞ |
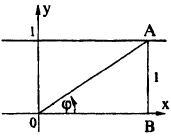
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos 
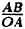
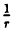
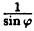
Пример:
Постройте линию, описываемую уравнением, у =
Решение:
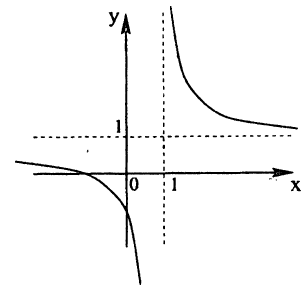
Сначала построим график функции у = 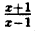
Наконец, строим линию описываемую уравнением у = 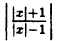
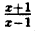
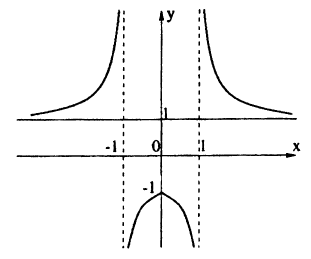
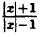
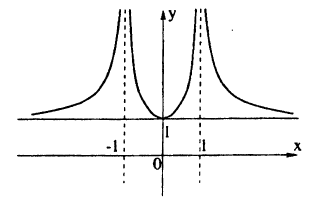
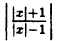
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =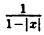
Пример:
Решение:
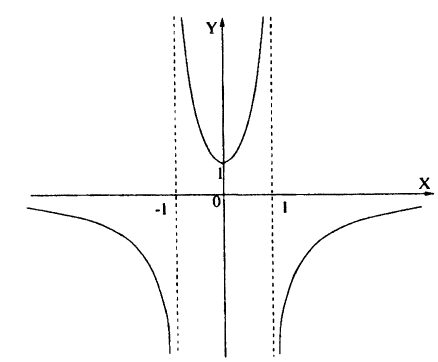
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
График функции y=f(kx)
Растяжение и сжатие — один из видов геометрических преобразований, благодаря которому на основе графиков элементарных функций можно легко строить графики многих других функций.
График функции y=f(kx) (где k>1) может быть получен из графика функции y=f(x) сжатием к оси Oy в k раз.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x/k; y) графика y=f(kx):
(то есть абсциссу (x) каждой точки начального графика уменьшаем в k раз, а ординату (y) оставляем без изменения. При этом точка, лежащая на оси Oy, остаётся на месте (так как 0:k=0).
1) График функции y=(2x)² можно получить из графика функции y=x ² с помощью сжатия к оси Oy в 2 раза.
На координатной плоскости строим график функции y=x² (можно отметить только его базовые точки). Затем координату x каждой точки делим на 2, а координату y оставляем без изменения. Таким образом, каждая точка нового графика становится ближе в 2 раза к оси Oy, чем точка начального графика (от оси Ox обе точки находятся на одинаковом расстоянии):
График y=(2x)² из графика y=x²
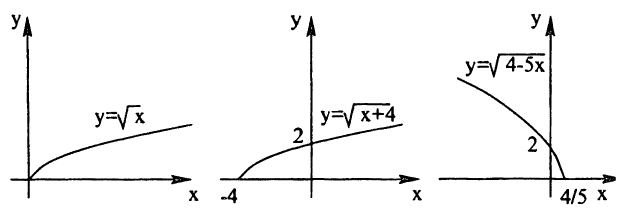
2) График функции y=√(5x) можно получить, сжав график функции y= √ x к оси Oy в 5 раз:
3) График функции y=|4х| может быть получен из графика функции y=|х| сжатием к оси Oy в 4 раза:
Преобразование графиков применяется при решении примеров из различных разделов алгебры.
Растяжение и сжатие графиков функций
Список функций, изученных в 7 и 8 классе
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$y_2 = y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX

График сжимается в 2 раза по оси OX
$y_2=y_1 при x_2 = \frac<1> <2>x_1$
График сжимается в 2 раза по оси OX
Теперь сравним пары функций с делением на p:
$ y_2 = f \left(\frac
$y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX

$y_2 = f \left(\frac
$ y_2 = y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
$y_2=y_1 при x_2 = 2x_1$
График растягивается в 2 раза по оси OX
При сравнении графиков двух функций
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY

$ y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
$y_2 = 2y_1 при x_2 = x_1$
График растягивается в 2 раза по оси OY
Теперь сравним пары функций с делением на A:
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY

$ y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
$y_2 = \frac<1><2>y_1 при x_2 = x_1$
График сжимается в 2 раза по оси OY
При сравнении графиков двух функций
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
Пример 2*. Постройте в одной координатной плоскости графики функций:
Памятка «Преобразование графиков функций»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ
Государственное автономное профессиональное образовательное
учреждение «Бузулукский строительный колледж»
г. Бузулука Оренбургской области
Выполнил: студент группы № 14 Поршин Артем,
ПАМЯТКА
«Алгоритм преобразования графиков функций – растяжение и сжатие вдоль осей координат»
Сжатие (растяжение) графика к (от) оси ординат.
Сначала изобразим график синуса, его период равен: T = 2π
Мысленно возьмём синусоиду в руки и сожмём её к оси Oy в 2 раза:
То есть, график функции y = sin 2 x получается путём сжатия графика y = sin x к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: T = π
2. Растяжение графика функции от оси ординат
Пример 2. Построить график функции
Берём в руки нашу «бесконечную гармошку»:
И растягиваем её от оси Oy в 2 раза:
То есть, график функции получается путём растяжения графика y = sin x от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: T = 4π.
Сжатие (растяжение) графика к (от) оси абсцисс
1. Если ФУНКЦИЯ f ( x ) умножается на число m >1, то происходит растяжение её графика вдоль оси ординат.
Пример 3 Построить график функции y = 2 sin x .
Рисуем график функции y = sin x
А теперь вытягиваем её вдоль оси Оу в 2 раза:
Период функции y = 2 sin x не изменился и составляет Т = 2π, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: Е = [-2; 2].
2. Если ФУНКЦИЯ умножается на число 0 m
Пример 4. Построить график функции y = sin x
Рисуем график функции y = sin x
Теперь сожмём синусоиду вдоль оси Оу в 2 раза:
Аналогично, период Т = 4π не изменился, но область значений функции «сплющилась» в два раза:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-907273
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Онлайн-конференция о профориентации и перспективах рынка труда
Время чтения: 3 минуты
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
Школьников Улан-Удэ перевели на удаленку из-за гриппа и ОРВИ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.