Что значит сумма целочисленное значение
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
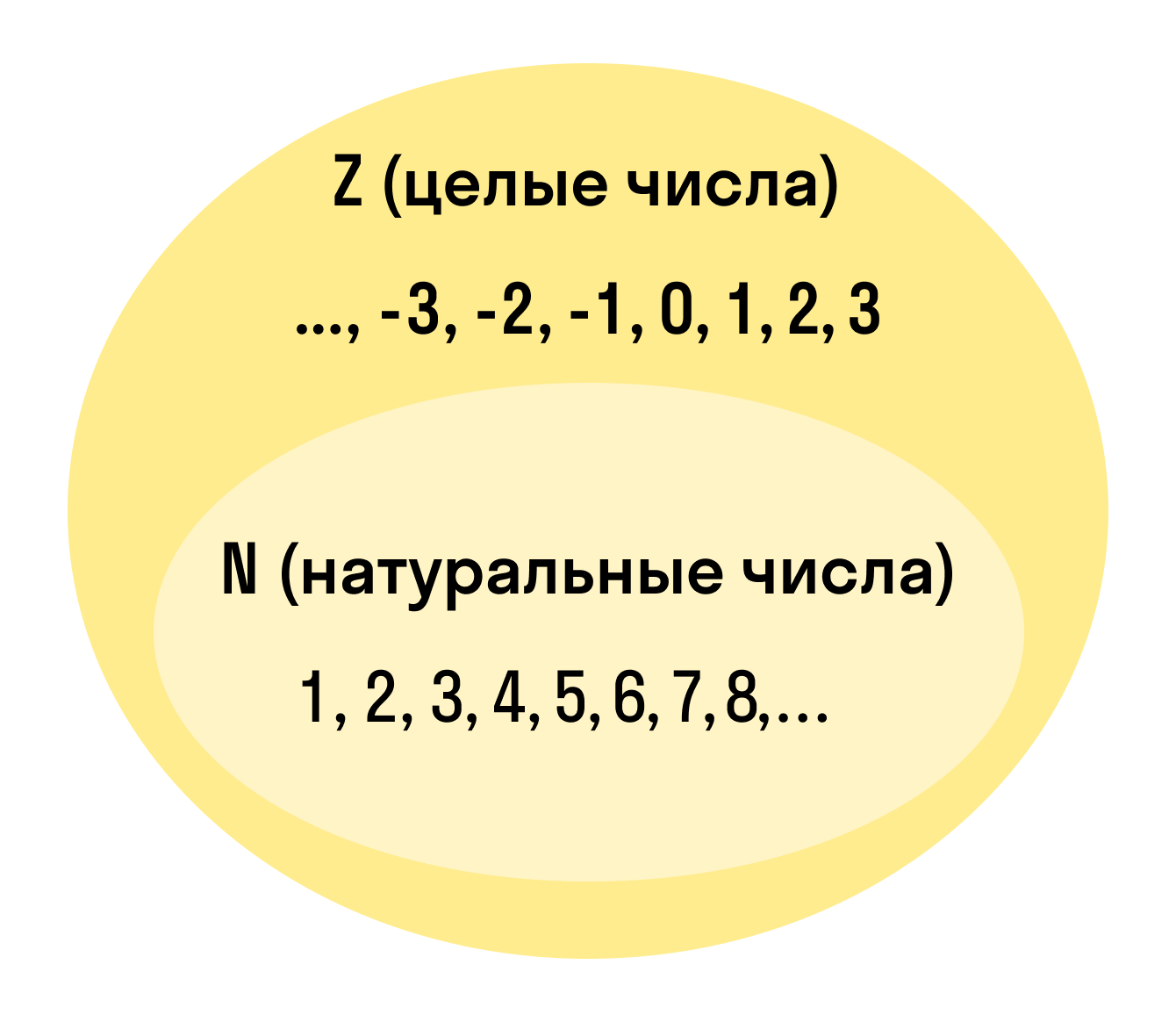
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Что такое целое число
Определение целого числа
Целыми числами называются все натуральные числа, все числа противоположные им по знаку и нуль.
На множестве целых чисел можно ввести четыре арифметические операции: сложение, вычитание, умножение и деление.
Сложение целых чисел
Подробнее о сложении чисел читайте по ссылке.
Задание. Вычислить сумму целых чисел:
2) первое слагаемое положительное, а второе отрицательное и модуль второго слагаемого больше модуля первого слагаемое, поэтому сумма будет равна
3) первое слагаемое отрицательное, а второе положительное и модуль второго слагаемого больше первого, сумма при этом будет равна
4) оба слагаемых отрицательные числа, таким образом, их сумма равна
Ответ.
Умножение целых чисел
Подробнее о умножении чисел читайте по ссылке.
Что такое целое число не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти произведение целых чисел:
$1)5 \cdot 9 \quad;\quad 2 ) 5 \cdot(-9) \quad;\quad 3 )-5 \cdot(-9) \quad;\quad 4 ) 5 \cdot 0$
2) первый множитель положительный, а второй отрицательный, произведение будет также числом отрицательным:
3) оба множителя отрицательные, следовательно, их произведение число положительное:
$$-5 \cdot(-9)=|-5| \cdot|-9|=5 \cdot 9=45$$
4) при умножении на нуль всегда в результате получаем нуль:
Ответ.
Вычитание целых чисел
Подробнее о вычитании чисел читайте по ссылке.
Задание. Найти разность чисел:
$1 )-27-13 \quad;\quad 2 ) 27-(-5)$
Решение. По правилу вычитания целых чисел первое выражение примет вид:
По правилу сложения целых чисел это равно:
Второе выражение запишется в виде:
Ответ.
Деление целых чисел
4.4 – Целочисленные типы данных со знаком
| Тип | Минимальный размер | Примечание |
|---|---|---|
| short | 16 бит | |
| int | 16 бит | На современных архитектурах размер обычно составляет 32 бита |
| long | 32 бита | |
| long long | 64 бита |
Ключевое различие между различными целочисленными типами заключается в том, что они имеют разные размеры – бо́льшие целочисленные типы могут содержать больши́е числа.
Напоминание
C++ гарантирует только то, что целочисленные типы будут иметь определенный минимальный размер, а не то, что они будут иметь конкретный размер. Для получения информации о том, как определить размер каждого типа на вашем компьютере, смотрите урок «4.3 – Размеры объектов и оператор sizeof ».
Целочисленные значения со знаком
По умолчанию целочисленные значения со знаком, что означает, что знак числа сохраняется. Следовательно, целочисленное значение со знаком может содержать как положительные, так и отрицательные числа (и 0).
В этом уроке мы сосредоточимся на целочисленных значениях со знаком. Беззнаковые целочисленные значения (которые могут содержать только неотрицательные числа) мы обсудим в следующем уроке.
Определение целочисленных значений со знаком
Ниже показан предпочтительный способ определения четырех типов целочисленных значений со знаком:
Все целочисленные значения (кроме int ) могут иметь необязательный суффикс int :
Целочисленные типы также могут принимать необязательное ключевое слово signed (т.е. со знаком), которое по соглашению обычно помещается перед именем типа:
Однако это ключевое слово так же не следует использовать, поскольку оно избыточно, так как по умолчанию целочисленные значения уже со знаком.
Лучшая практика
Диапазоны целочисленных значений со знаком
Как вы узнали в предыдущем разделе, переменная размером n бит может содержать 2 n возможных значений. Но каких именно значений? Набор конкретных значений, которые тип данных может принимать, мы называем его диапазоном. Диапазон целочисленной переменной определяется двумя факторами: ее размером (в битах) и тем, со знаком она или нет.
В качестве отступления.
Ниже показана таблица, содержащая диапазон целочисленных значений со знаком разных размеров:
Для тех, кто не склонен к математике… воспользуйтесь таблицей. 🙂
Переполнение целочисленных значений
Что произойдет, если мы попытаемся присвоить значение 280 8-битному целочисленному значению со знаком? Это число выходит за пределы диапазона, который может содержать 8-битовое целочисленное значение со знаком. Для числа 280 требуется 9 бит (плюс 1 бит для знака), но в 8-битном целочисленном значении со знаком у нас есть только 7 бит (плюс 1 бит для знака).
Переполнение целочисленных значений (часто для краткости называемое просто переполнением) происходит, когда мы пытаемся сохранить значение, выходящее за пределы диапазона типа. По сути, число, которое мы пытаемся сохранить, требует для представления большее количества бит, чем доступно объекту. В таком случае данные теряются, потому что объекту для хранения всего не хватает памяти.
В случае целочисленных значений со знаком, какие биты теряются, точно не определено, таким образом, переполнение целочисленного значения со знаком приводит к неопределенному поведению.
Предупреждение
Переполнение целочисленного значения со знаком приведет к неопределенному поведению.
Как правило, переполнение приводит к потере информации, что почти никогда не бывает желательно. Если есть подозрение, что объекту может потребоваться сохранить значение, выходящее за пределы его диапазона, используйте тип с большим диапазоном!
Деление целочисленных значений
При делении двух целочисленных значений, когда частное представляет собой целое число, C++ работает так, как вы ожидаете:
Это дает ожидаемый результат:
Но давайте посмотрим, что происходит, когда целочисленное деление приводит к дробному результату:
Это дает, возможно, неожиданный результат:
При делении двух целочисленных значений (так называемое целочисленное деление) C++ всегда дает целочисленный результат. Поскольку целые числа не могут содержать дробные значения, любая дробная часть просто отбрасывается (не округляется!).
Предупреждение
Будьте осторожны при использовании целочисленного деления, так как вы потеряете дробную часть частного. Однако, если это то, что вам нужно, то целочисленное деление использовать можно, так как результаты предсказуемы.
Если вам необходимы дробные результаты, мы покажем способ их получить в уроке «5.2 – Арифметические операторы».
целочисленная сумма
Смотреть что такое «целочисленная сумма» в других словарях:
ЛОГАРИФМ — число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление вычитанием, возведение в степень… … Энциклопедия Кольера
УЗЛОВ КОБОРДИЗМ — (правильнее бордизм узлов, см. Бордизм) отношение эквивалентности на множестве узлов, более слабое, чем изотопич. тип. Два гладких n мерных узла и наз. кобордантными, если существует гладкое ориентированное (n+1) мерное подмногообразие V… … Математическая энциклопедия
Унарная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
УЗЛОВ И ЗАЦЕПЛЕНИЙ КВАДРАТИЧНЫЕ ФОРМЫ — формы, сопоставляемые трехмерным узлам и зацеплениям; нек рые инварианты этих форм являются топологич. инвариантами изотопич. типа узлов и зацеплений. У. и з. к. ф. возникают в результате симметризации спариваний Зейферта (см. Зейферта матрица).… … Математическая энциклопедия
ДЕДЕКИНДОВА РЕШЕТКА — дедекиндова структура, модулярная решетка (структура), решетка, в к рой справедлив модулярный закон, т. е. влечет (a+b)c=а+bс для всякого Ь. Высказанное требование равносильно справедливости тождества ( ас+b) с=ас+bс. Примерами Д. р. служат… … Математическая энциклопедия
ПЛОЩАДЬ — численная характеристика, приписываемая плоским фигурам определенного класса (напр., многоугольникам) и обладающая следующими свойствами: 1) П. неотрицательна; 2) П. аддитивна (в случае многоугольников это означает, что если фигура составлена из… … Математическая энциклопедия
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Математическая формула — Эта статья об обозначениях элементарной математики; Для более общего контекста см.: Математические обозначения. Математическая формула (от лат. formula уменьшительное от forma образ, вид) принятая в математике (а также… … Википедия
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия
Числа. Целые числа. Свойства целых чисел.
Целые числа – это натуральные числа, а также противоположные им числа и нуль.
Целые числа — расширение множества натуральных чисел N, которое получается путем добавления к N 0 и отрицательных чисел типа − n. Множество целых чисел обозначают Z.
Сумма, разность и произведение целых чисел дают снова целые числа, т.е. целые числа составляют кольцо относительно операций сложения и умножения.
Целые числа на числовой оси:
Сколько целых чисел? Какое количество целых чисел? Самого большого и самого маленького целого числа нет. Этот ряд бесконечен. Наибольшее и наименьшее целое число не существует.
Натуральные числа еще называются положительными целыми числами, т.е. фраза «натуральное число» и «положительное целое число» это одно и то же.
Ни обыкновенные, ни десятичные дроби не являются целыми числами. Но существуют дроби с целыми числами.
Операции над целыми числами.
1. Сумма целых чисел.
Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.
2. Вычитание целых чисел.
Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.
3. Умножение целых чисел.
Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.
Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.
(–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).
4. Деление целых чисел.
Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.
Свойства целых чисел.
Z не замкнуто относительно деления 2-х целых чисел (например, 1/2). Ниже приведенная таблица показывает некоторые основные свойства сложения и умножения для любых целых a, b и c.