Что значит средневзвешенное значение

СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)

Смотреть что такое «СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ)» в других словарях:

среднее значение величины — 3.14 среднее значение величины: Средневзвешенное значение величины за определенный период времени (час, сутки). Источник … Словарь-справочник терминов нормативно-технической документации

СРЕДНЕВЗВЕШЕННОЕ — (weighted average) Среднее арифметическое значение, в котором учтен вес каждого из слагаемых, для которых рассчитывается это среднее значение. Например, если кто то покупает товар тремя партиями, одна из которых – 100 тонн по 70 ф. ст. за тонну,… … Словарь бизнес-терминов

среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 … Словарь-справочник терминов нормативно-технической документации

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

средневзвешенное значение — svertinis vidurkis statusas T sritis fizika atitikmenys: angl. weighted arithmetic average; weighted average; weighted mean vok. gewogener Mittelwert, m; gewogenes Mittel, n rus. взвешенное среднее, n; средневзвешенное значение, n pranc. moyenne… … Fizikos terminų žodynas

взвешенное арифметическое среднее — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

взвешенное среднее — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

взвешенное арифметическое среднее — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

взвешенное среднее — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

Источник

Средневзвешенное значение — формула в Excel

В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.

Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.

Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?

Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.

В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.

Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.

Что такое средневзвешенное значение?

Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.

В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.

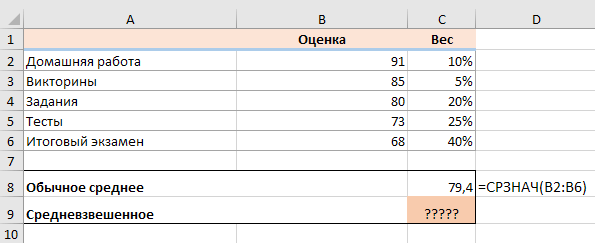
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:

((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8

Формулы для средневзвешенного значения в Excel

В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.

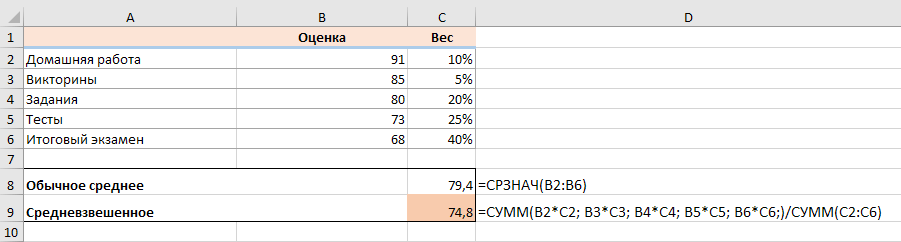
Пример 1. Функция СУММ.

По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.

Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).

Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.

В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.

Пример 2. Функция СУММПРОИЗВ

Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.

Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:

= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )

Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.

Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.

В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:

Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.

Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:

Видите, в этом случае мы обошлись без процентов.

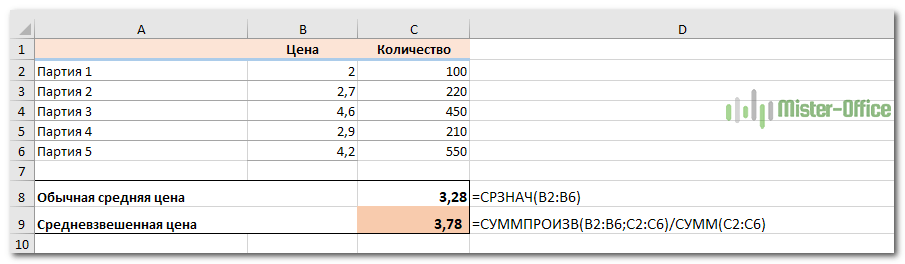
Пример 3. Средневзвешенная цена.

Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.

Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.

Ну, это все о формуле средневзвешенного значения в Excel.

Источник

Средневзвешенное

Опубликовано 22.05.2020 · Обновлено 22.05.2021

Что такое Средневзвешенное?

Средневзвешенное значение – это расчет, который учитывает различную степень важности чисел в наборе данных. При вычислении средневзвешенного значения каждое число в наборе данных умножается на заранее определенный вес перед окончательным расчетом.

Средневзвешенное значение может быть более точным, чем простое среднее, в котором всем числам в наборе данных присваивается одинаковый вес.

Понимание средневзвешенных значений

При вычислении простого среднего или среднего арифметического все числа обрабатываются одинаково, и им присваивается одинаковый вес. Но средневзвешенное значение присваивает веса, которые заранее определяют относительную важность каждой точки данных.

Ключевые моменты

Средневзвешенное значение чаще всего вычисляется для выравнивания частоты значений в наборе данных. Например, опрос может собрать достаточно ответов от каждой возрастной группы, чтобы считаться статистически достоверным, но возрастная группа 18-34 может иметь меньше респондентов, чем все остальные, по отношению к их доле в населении. Команда опроса может взвесить результаты возрастной группы 18-34 года, чтобы их взгляды были представлены пропорционально.

Однако значения в наборе данных могут быть взвешены по другим причинам, кроме частоты появления. Например, если ученики в танцевальном классе оцениваются по навыкам, посещаемости и манерам, оценка по навыкам может иметь больший вес, чем другие факторы.

В любом случае при средневзвешенном значении каждое значение точки данных умножается на назначенный вес, который затем суммируется и делится на количество точек данных.

В средневзвешенном значении окончательное среднее число отражает относительную важность каждого наблюдения и, таким образом, является более информативным, чем простое среднее. Это также имеет эффект сглаживания данных и повышения их точности.

Взвешивание портфеля акций

Инвесторы обычно создают позицию в акции в течение нескольких лет. Это затрудняет отслеживание стоимости этих акций и их относительных изменений в стоимости.

Инвестор может рассчитать средневзвешенную цену акций, уплаченных за акции. Для этого умножьте количество акций, приобретенных по каждой цене, на эту цену, сложите эти значения и затем разделите общую стоимость на общее количество акций.

Краткая справка

Средневзвешенное значение достигается путем предварительного определения относительной важности каждой точки данных.

Например, предположим, что инвестор приобретает 100 акций компании в первый год по цене 10 долларов США и 50 акций той же компании во второй год по цене 40 долларов США. Чтобы получить средневзвешенное значение уплаченной цены, инвестор умножает 100 акций на 10 долларов для первого года и 50 акций на 40 долларов для второго года, а затем складывает результаты, чтобы получить в сумме 3000 долларов. Затем общая сумма, уплаченная за акции, в данном случае 3000 долларов, делится на количество акций, приобретенных за оба года, 150, чтобы получить средневзвешенную цену в размере 20 долларов.

Теперь это среднее значение взвешивается по количеству акций, приобретенных по каждой цене, а не только по абсолютной цене.

Примеры средневзвешенных значений

Средневзвешенные значения появляются во многих областях финансов, помимо покупной цены акций, включая доходность портфеля, учет запасов и оценку.

Когда фонд, владеющий несколькими ценными бумагами, увеличивается на 10 процентов за год, эти 10 процентов представляют собой средневзвешенную доходность фонда по отношению к стоимости каждой позиции в фонде.

Для учета запасов средневзвешенная стоимость запасов учитывает колебания цен на товары, например, в то время как методы LIFO (последний пришел – первый ушел) или FIFO (первый пришел – первый ушел) придает большее значение времени, чем стоимости.

При оценке компаний, чтобы определить, правильно ли установлена ​​цена на их акции, инвесторы используют средневзвешенную стоимость капитала (WACC) для дисконтирования денежных потоков компании. WACC взвешивается на основе рыночной стоимости долга и капитала в структуре капитала компании.

Источник

Средневзвешенное арифметическое

СОДЕРЖАНИЕ

Примеры [ править ]

Базовый пример [ править ]

Учитывая два школьных класса, один с 20 учениками и один с 30 учениками, оценки в каждом классе по тесту были:

Икс ¯ знак равно 4300 50 знак равно 86. <\ displaystyle <\ bar > = <\ frac <4300><50>> = 86.>

Или это может быть достигнуто путем взвешивания средних значений класса по количеству учеников в каждом классе. Большему классу придается больший «вес»:

Икс ¯ знак равно ( 20 × 80 ) + ( 30 × 90 ) 20 + 30 знак равно 86. <\ displaystyle <\ bar > = <\ frac <(20 \ times 80) + (30 \ times 90)><20 + 30>> = 86.>

Таким образом, взвешенное среднее позволяет найти среднюю среднюю оценку учащегося, не зная оценки каждого учащегося. Требуются только средства класса и количество учеников в каждом классе.

Пример выпуклой комбинации [ править ]

Используя предыдущий пример, мы получили бы следующие веса:

Затем примените такие веса:

Икс ¯ знак равно ( 0,4 × 80 ) + ( 0,6 × 90 ) знак равно 86. <\ displaystyle <\ bar > = (0,4 \ times 80) + (0,6 \ times 90) = 86.>

Математическое определение [ править ]

который расширяется до:

Следовательно, элементы данных с большим весом вносят больший вклад в средневзвешенное значение, чем элементы с низким весом. Вес не может быть отрицательным. Некоторые из них могут быть равны нулю, но не все (так как деление на ноль недопустимо).

Тогда для таких нормированных весов средневзвешенное значение будет:

x ¯ = ∑ i = 1 n w i ′ x i <\displaystyle <\bar >=\sum _^‘x_>> .

Обратите внимание, что всегда можно нормализовать веса, сделав следующее преобразование исходных весов:

w i ′ = w i ∑ j = 1 n w j <\displaystyle w_‘=<\frac ><\sum _^>>>> .

Использование нормализованного веса дает те же результаты, что и при использовании исходных весов:

σ x ¯ = ( ∑ i = 1 n w i ) − 1 <\textstyle \sigma _<\bar >=\left(<\sqrt <\sum _^>>>\right)^<-1>>

Статистические свойства [ править ]

Взвешенное значение выборки, само по себе является случайной величиной. Его ожидаемое значение и стандартное отклонение связаны с ожидаемыми значениями и стандартными отклонениями наблюдений следующим образом. Для простоты мы предполагаем нормализованные веса (веса, суммирующие единицу). x ¯ <\displaystyle <\bar >>

Если наблюдения имеют ожидаемые значения

тогда средневзвешенное значение выборки имеет ожидание

В частности, если средние равны, то математическое ожидание средневзвешенного выборочного среднего будет этим значением, μ i = μ <\displaystyle \mu _=\mu >

Для некоррелированных наблюдений с дисперсиями дисперсия средневзвешенного значения выборки [ необходима ссылка ] σ i 2 <\displaystyle \sigma _^<2>>

σ x ¯ 2 = ∑ i = 1 n w i ′ 2 σ i 2 <\displaystyle \sigma _<\bar >^<2>=\sum _^‘^<2>\sigma _^<2>>>

Следовательно, если все наблюдения имеют одинаковую дисперсию, средневзвешенное значение выборки будет иметь дисперсию σ i 2 = σ 0 2 <\displaystyle \sigma _^<2>=\sigma _<0>^<2>>

Веса дисперсии [ править ]

Средневзвешенное значение в этом случае:

а стандартная ошибка средневзвешенного значения (с весами дисперсии) составляет:

Приведенные выше уравнения можно объединить, чтобы получить:

Значение этого выбора состоит в том, что это взвешенное среднее является оценкой максимального правдоподобия среднего значения распределений вероятностей в предположении, что они независимы и нормально распределены с одним и тем же средним значением.

Исправление чрезмерной или недостаточной дисперсии [ править ]

Взвешенные средние обычно используются для нахождения средневзвешенного значения исторических данных, а не теоретически сгенерированных данных. В этом случае будет некоторая ошибка в дисперсии каждой точки данных. Обычно экспериментальные ошибки могут быть недооценены из-за того, что экспериментатор не принимает во внимание все источники ошибок при вычислении дисперсии каждой точки данных. В этом случае необходимо скорректировать дисперсию средневзвешенного значения, чтобы учесть тот факт, что оно слишком велико. Исправление, которое необходимо сделать, это χ 2 <\displaystyle \chi ^<2>>

σ ^ x ¯ 2 = σ x ¯ 2 χ ν 2 <\displaystyle <\hat <\sigma >>_<\bar >^<2>=\sigma _<\bar >^<2>\chi _<\nu >^<2>>

где это уменьшенный хи-квадрат : χ ν 2 <\displaystyle \chi _<\nu >^<2>>

χ ν 2 = 1 ( n − 1 ) ∑ i = 1 n ( x i − x ¯ ) 2 σ i 2 ; <\displaystyle \chi _<\nu >^<2>=<\frac <1><(n-1)>>\sum _^<\frac <(x_—<\bar >)^<2>><\sigma _^<2>>>;>

Проверка загрузки [ править ]

Методами начальной загрузки было показано, что следующая точная оценка квадрата стандартной ошибки среднего (общий случай): [1]

σ x ¯ 2 = n ( n − 1 ) w s 2 [ ∑ ( w i x i − w s x ¯ ) 2 − 2 x ¯ ∑ ( w i − w s ) ( w i x i − w s x ¯ ) + x ¯ 2 ∑ ( w i − w s ) 2 ] <\displaystyle \sigma _<\bar >^<2>=<\frac <(n-1)w_^<2>>>\left[\sum (w_x_-w_<\bar >)^<2>-2<\bar >\sum (w_-w_)(w_x_-w_<\bar >)+<\bar >^<2>\sum (w_-w_)^<2>\right]>

σ x ¯ 2 = n ( n − 1 ) w s 2 ∑ w i 2 ( x i − x ¯ ) 2 <\displaystyle \sigma _<\bar >^<2>=<\frac <(n-1)w_^<2>>>\sum w_^<2>(x_—<\bar >)^<2>>

Взвешенная дисперсия выборки [ править ]

Смещен взвешенная дисперсия выборки определяются аналогично обычной необъективной выборочной дисперсия : σ ^ w 2 <\displaystyle <\hat <\sigma >>_ <\mathrm >^<2>> σ ^ 2 <\displaystyle <\hat <\sigma >>^<2>>

σ ^ 2 = ∑ i = 1 N ( x i − μ ) 2 N σ ^ w 2 = ∑ i = 1 N w i ( x i − μ ∗ ) 2 V 1 <\displaystyle <\begin<\hat <\sigma >>^<2>\ &=<\frac <\sum \limits _^\left(x_-\mu \right)^<2>>>\\<\hat <\sigma >>_ <\mathrm >^<2>&=<\frac <\sum \limits _^w_\left(x_-\mu ^<*>\right)^<2>>>>\end>>

Веса частоты [ править ]

Если веса являются частотными весами (где вес равен количеству вхождений), то несмещенная оценка:

s 2 = ∑ i = 1 N w i ( x i − μ ∗ ) 2 V 1 − 1 <\displaystyle <\begins^<2>\ &=<\frac <\sum \limits _^w_\left(x_-\mu ^<*>\right)^<2>>-1>>\end>>

Это эффективно применяет поправку Бесселя для частотных весов.

Если частотные веса нормализованы к 1, то правильное выражение после поправки Бесселя станет < w i ><\displaystyle \\>>

s 2 = V 1 V 1 − 1 ∑ i = 1 N w i ( x i − μ ∗ ) 2 <\displaystyle <\begins^<2>\ &=<\frac >-1>>\sum _^w_\left(x_-\mu ^<*>\right)^<2>\end>>

Веса надежности [ править ]

E ⁡ [ σ ^ 2 ] = ∑ i = 1 N E ⁡ [ ( x i − μ ) 2 ] N = E ⁡ [ ( X − E ⁡ [ X ] ) 2 ] − 1 N E ⁡ [ ( X − E ⁡ [ X ] ) 2 ] = ( N − 1 N ) σ actual 2 E ⁡ [ σ ^ w 2 ] = ∑ i = 1 N w i E ⁡ [ ( x i − μ ∗ ) 2 ] V 1 = E ⁡ [ ( X − E ⁡ [ X ] ) 2 ] − V 2 V 1 2 E ⁡ [ ( X − E ⁡ [ X ] ) 2 ] = ( 1 − V 2 V 1 2 ) σ actual 2 <\displaystyle <\begin\operatorname [<\hat <\sigma >>^<2>]&=<\frac <\sum \limits _^\operatorname [(x_-\mu )^<2>]>>\\&=\operatorname [(X-\operatorname [X])^<2>]-<\frac <1>>\operatorname [(X-\operatorname [X])^<2>]\\&=\left(<\frac >\right)\sigma _<\text>^<2>\\\operatorname [<\hat <\sigma >>_ <\mathrm >^<2>]&=<\frac <\sum \limits _^w_\operatorname [(x_-\mu ^<*>)^<2>]>>>\\&=\operatorname [(X-\operatorname [X])^<2>]-<\frac >^<2>>>\operatorname [(X-\operatorname [X])^<2>]\\&=\left(1-<\frac >^<2>>>\right)\sigma _<\text>^<2>\end>>

Окончательная объективная оценка дисперсии выборки:

s w 2 = σ ^ w 2 1 − ( V 2 / V 1 2 ) = ∑ i = 1 N w i ( x i − μ ∗ ) 2 V 1 − ( V 2 / V 1 ) <\displaystyle <\begins_ <\mathrm >^<2>\ &=<\frac <<\hat <\sigma >>_ <\mathrm >^<2>><1-(V_<2>/V_<1>^<2>)>>\\&=<\frac <\sum \limits _^w_(x_-\mu ^<*>)^<2>>-(V_<2>/V_<1>)>>\end>> , [2]

В качестве примечания, были описаны другие подходы для вычисления взвешенной дисперсии выборки. [3]

Ковариация взвешенной выборки [ править ]

Тогда вектор взвешенного среднего определяется как μ ∗ <\displaystyle \textstyle \mathbf <\mu ^<*>> >

Матрица взвешенной ковариации имеет следующий вид: [4]

Как и в случае взвешенной выборочной дисперсии, существуют две разные несмещенные оценки в зависимости от типа весов.

Веса частоты [ править ]

Веса надежности [ править ]

V 1 = ∑ i = 1 N w i = 1. <\displaystyle V_<1>=\sum _^w_=1.>

(Если это не так, разделите веса на их сумму для нормализации перед вычислением : V 1 <\displaystyle V_<1>>

w i ′ = w i ∑ i = 1 N w i <\displaystyle w_‘=<\frac ><\sum _^w_>>>

Тогда вектор взвешенного среднего можно упростить до μ ∗ <\displaystyle \textstyle \mathbf <\mu ^<*>> >

Рассуждения здесь те же, что и в предыдущем разделе.

Поскольку мы предполагаем, что веса нормализованы, это сводится к следующему: V 1 = 1 <\displaystyle V_<1>=1>

Если все веса одинаковы, т. Е. Тогда взвешенное среднее и ковариация сводятся к невзвешенному выборочному среднему и ковариации, указанным выше. w i / V 1 = 1 / N <\displaystyle \textstyle w_/V_<1>=1/N>

Векторные оценки [ править ]

Средневзвешенное значение в этом случае:

(где порядок произведения матрица-вектор не коммутативен ) в терминах ковариации взвешенного среднего:

Например, рассмотрим средневзвешенное значение точки [1 0] с высокой дисперсией во втором компоненте и [0 1] с высокой дисперсией в первом компоненте. потом

тогда средневзвешенное значение:

x ¯ = ( C 1 − 1 + C 2 − 1 ) − 1 ( C 1 − 1 x 1 + C 2 − 1 x 2 ) = [ 0.9901 0 0 0.9901 ] [ 1 1 ] = [ 0.9901 0.9901 ] <\displaystyle <\begin <\bar <\mathbf >>&=\left(\mathbf _<1>^<-1>+\mathbf _<2>^<-1>\right)^<-1>\left(\mathbf _<1>^<-1>\mathbf _<1>+\mathbf _<2>^<-1>\mathbf _<2>\right)\\[5pt]&=<\begin0.9901&0\\0&0.9901\end><\begin1\\1\end>=<\begin0.9901\\0.9901\end>\end>>

что имеет смысл: оценка [1 0] «совместима» во втором компоненте, а оценка [0 1] согласована в первом компоненте, поэтому взвешенное среднее почти равно [1 1].

Учет корреляций [ править ]

Снижение силы взаимодействия [ править ]

Экспоненциально убывающие веса [ править ]

Средневзвешенные функции [ править ]

Понятие средневзвешенного значения можно распространить на функции. [7] Средневзвешенные функции играют важную роль в системах взвешенного дифференциального и интегрального исчисления. [8]

Источник