Что значит сравнение натуральных чисел
Сравнение натуральных чисел
Вам уже известно, что натуральные числа используются для обозначения количества тех или иных предметов. Возьмем, к примеру, конфеты. Мама купила шоколадные батончики и высыпала их кучкой на столе. Дети пересчитали, и их оказалось 25 штук.
Пришел с работы папа и высыпает рядом еще конфеты. На первый взгляд, эта кучка не отличается от первой, но пересчитав количество папиных конфет, дети увидели, что их всего 23. Значит, эти кучки разные. Чтобы это выяснить, дети произвели два действия:
Сравнить натуральные числа – это означает узнать, отличаются ли они друг от друга или они одинаковые. Если сравниваемые числа отличаются, тогда мы может узнать, что одно число больше другого, а второе, соответственно, меньше первого.
Как сравнить натуральные числа
Сравнить натуральные числа можно такими способами:
В результате сравнения мы можем получить:
Равенство натуральных чисел
Если два натуральных числа имеют полностью одинаковую запись, то и записанные с их помощью числа одинаковы (говорят просто – они равны). Если их записи отличаются, тогда эти числа не равны.
Если мы определили, что числа не равны, тогда нам необходимо выяснить, какое положение они занимают по отношению друг к другу, большее или меньшее.
Запись и чтение неравенств
Неравенство – это запись чисел или математических выражений, которая содержит знаки неравенства.
Читается подобная запись следующим образом. Первое число называется в именительном падеже (кто? что?), а второе в родительном (кого? чего?). Например, так: «два меньше четырех», «восемьдесят девять больше семидесяти восьми».
Если стрелка смотрит влево: « меньше » и означает, что слева от него находится число меньшее, чем справа.
Если стрелка смотрит вправо: «>», такой знак называется « больше » и означает, что слева от него находится большее число, чем справа.
Стрелка знака всегда указывает на меньшее число, а двойная вилка – на большее!
Например, дано неравенство 5 верным (правильно отмеченным), например, 1 неверным (неправильно отмеченным), например, 5>6.
Сравнение однозначных натуральных чисел с помощью ряда
Этот способ лучше всего подходит для сравнения однозначных натуральных чисел.
Меньшим называют число, которое в натуральном ряду находится раньше другого, а большим – то, которое расположено позже другого.
Например, число 2 в натуральном ряду стоит раньше, чем число 4, значит, 2 8.
Число 1 (единица) – самое меньшее из натуральных чисел, поскольку стоит в натуральном ряду первым.
На координатном луче меньшее число обозначается раньше (левее), а большее число – позже (правее) другого числа.
Рис. 1. Большее и меньшее число на координатном луче.
Действительно, чем больше в числе цифр, тем выше разряд самой первой цифры в этом числе.
К примеру, 123456>12345, потому что в первом числе цифра 1 обозначает сотню тысяч, а во втором – десяток тысяч.
Поэтому, для решения задач на сравнение чисел с разным количеством цифр, из которых они состоят, нам достаточно сравнить эти количества:
123456 – шестизначное число, 6 цифр;
12345 – пятизначное число, 5 цифр;
Например, сравним два числа: 12336 и 12345. Оба числа пятизначные. Значит, сравниваем каждую цифру, начиная с 5 разряда (десятков тысяч):
Сравнение двух, трех, и более чисел
Сравнивать между собой можно не только два натуральных числа.
Вернемся к примеру с конфетами на столе. Бабушка тоже купила конфеты и высыпала их на столе. Дети пересчитали их, и в бабушкиной кучке оказалось 33 штуки. Количество конфет мы можем записать натуральными числами: 25, 23 и 33.
Сравнив их между собой, мы увидим три неравенства:
Гораздо удобнее записать результат сравнения в виде двойного неравенства :
23
Как видите, все неравенства верны.
Чтобы быстро записать двойное, тройное, и т.д. неравенство, нужно расставить данные числа слева направо в порядке возрастания (предварительно сравнив между собой), оставив небольшие промежутки между ними. А после этого в оставленные промежутки записать знаки
Урок 9 Бесплатно Меньше или больше
Вы уже знаете, что такое натуральное число и как оно записывается.
Также Вам известно, что такое координатный луч.
Сегодня мы применим эти знания, чтобы сформулировать понятия “больше” и “меньше” для натуральных чисел, научимся отвечать на вопрос, как соотносятся два натуральных числа.
Узнаем, как сравнивать числа с помощью координатного луча, как сравнивать натуральные числа с одинаковым и разным количеством знаков, разберем понятие “сортировка” для чисел.
Определение
Вспомним, как выглядит натуральный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9 …
Из двух натуральных чисел больше то, которое при счете называют позже.
Из двух натуральных чисел меньше то, которое при счете называют раньше.
Данное определение достаточно просто и понятно, посмотрим на примерах.
Например, как соотносятся 3 и 5?
Если мы посмотрим на натуральный ряд, то увидим, что 3 названо раньше, чем 5, следовательно, 3 меньше 5-ти.
Другой пример, как соотносятся числа 9 и 6?
Опять же, надо посмотреть на натуральный ряд, тогда можно увидеть, что 9 названо позже, чем 6, значит, 9 больше 6-ти.
Каждый раз писать словами “больше” или “меньше” может быть неудобно, поэтому удобно использовать знаки.
Знак “ ” читается как “больше”.
Таким образом, чтобы кратко записать, что 3 меньше 5-ти, достаточно написать “\(\mathbf<3 6>\)”.
Запись с использование знаком “больше” или “меньше” называют неравенством.
Довольно часто вопрос про соотношение двух чисел может ставится так: “какой знак должен стоять в неравенстве на месте пропуска”, а дальше идет неравенство с пропущенным знаком, например, такое: “4 _ 6”.
В данном случае надо ответить на вопрос, больше ли 4 6-ти или меньше, и поставить соответствующий знак.
Здесь первое число меньше второго и нужно поставить знак “ 0”, “2 > 0”, “3 > 0” и так далее для каждого натурального числа.
Пройти тест и получить оценку можно после входа или регистрации
ВОПРОСЫ
1. Что значит сравнить два различных натуральных числа?
2. Как, используя натуральный ряд, можно определить, какое из двух натуральных чисел меньше? Больше?
3. Какое число меньше любого натурального числа?
Число 0 меньше любого натурального числа.
4. Как сравнивать натуральные числа, имеющие разное количество цифр?
Из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше.
5. Какое из натуральных чисел с одинаковым количеством цифр больше?
Из двух натуральных чисел, имеющих одинаковое количество цифр, большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
6. Как на координатном луче расположена точка с меньшей координатой относительно точки с большей координатой?
На координатном луче точка с меньшей координатой расположена левее точки с большей координатой.
РЕШАЕМ УСТНО
1. Какое из чисел 516 и 615 расположено на координатном луче левее?
Число 516 расположено на координатном луче левее, чем число 615.
2. Какое из чисел 405 и 504 расположено на координатном луче правее?
Число 504 расположено на координатном луче правее, чем 405.
Цена деления термометра равна 2°С.
4. Вычислите:
5. В коробке лежат пять красных и три зеленых карандаша. Наугад из нее вынимают по одному карандашу. Какое наименьшее количество карандашей над взять, чтобы среди них были хотя бы два красных и один зеленый?
УПРАЖНЕНИЯ
142. Прочитайте неравенство:
143. Запишите в виде неравенства утверждение:
144. Сравните числа:
145. Сравните числа:
146. Расположите в порядке возрастания числа: 894, 479, 846, 591, 701.
479, 591, 701, 846, 894.
147. Расположите в порядке убывания числа: 639, 724, 731, 658, 693.
731, 724, 693, 658, 639.
148. Назовите все натуральные числа, которые: 1) больше 678, но меньше 684; 2) больше 935, но меньше 940; 3) больше 2 934 450, но меньше 2 934 454; 4) больше 12 706, но меньше 12 708; 5) больше 24 315, но меньше 24 316.
149. Запишите все натуральные числа, которые: 1) больше 549, но меньше 556; 2) больше 1 823 236, но меньше 1 823 240; 3) больше 47 246, но меньше 47 248.
150. Отметьте на координатном луче все натуральные числа которые: 1) меньше 12; 2) больше 4, но меньше 10.
151. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
152. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
153. 1) Запишите какое-либо натуральное число, которое больше 473 и меньше 664, содержащее цифру 5 в разряде десятков. Сколько таких чисел можно написать?
2) Запишите какое-либо натуральное число, которое больше 578, но меньше 638, содержащее цифру 6 в разряде сотен. Сколько таких чисел можно написать? запишите наименьшее и наибольшее из таких чисел.
154. Запишите какое-либо натуральное число, которое больше 2 364 и меньше 2 432, содержащее цифру 8 в разряде единиц. Сколько таких чисел можно написать? Запишите наименьшее и наибольшее из таких чисел.
157. Запишите в виде двойного неравенства утверждение: 1) число 7 больше 5 и меньше10; 2) число 62 меньше 0 и больше 60; 3) число 54 меньше 94 и больше 44; 4) число 128 больше 127 и меньше 129.
158. Запишите в виде двойного неравенства утверждения: 1) число 56 больше 52 и меньше 58; 2) число 258 больше 250 и меньше 261; 3) число 4 325 меньше 4 400 и больше 4 300; 4) число 999 999 меньше 1 000 000 и больше 555 558.
159. В записи чисел вместо нескольких цифр поставили звездочки. Сравните эти числа:
160. В записи чисел вместо нескольких цифр поставили звездочки. Сравните эти числа:
161. Сравните: 1) 2 км и 1 968 м; 2) 4 дм и 4 м; 3) 3 км 94 м и 3 126 м; 4) 712 кг и 8 ц; 5) 15 т и 35 ц; 6) 6 ц 23 кг и 658 кг; 7) 4 т 275 кг и 42 ц 75 кг; 8) 5 т 7 ц 36 кг и 5 т 863 кг; 9) 8 т и 81 ц; 10) 83 дм 7 см и 8 м 30 см.
162. Сравните: 1) 6 892 м и 7 км; 2) 8 см и 8 дм; 3) 4 км 43 м и 4 210 м; 4) 27 дм 3 см и 270 см; 5) 9 ц и 892 кг; 6) 2 ц 86 кг и 264 кг; 7) 3 т 248 кг и 32 ц 84 кг; 8) 12 т 2 кг и 120 ц 2 кг.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
163. Вычислите:
164. Из 24 м ткани можно сшить семь одинаковых платьев. Сколько таких платьев можно сшить из 48 м этой ткани?
165. Знаменитый университет Сорбонна, находящийся в Париже (Франция), основан в 1215 г. Он основан на 6 лет позже Кембриджского университета (Великобритания) и на 540 лет раньше Московского государственного университета имени М.В. Ломоносова. Определите год основания: 1) Кембриджского университета; 2) Московского государственного университета имени М.В. Ломоносова. Сколько лет исполняется в этом году Новосибирскому государственному университету, если Кембриджский университет основан раньше него на 750 лет?
ЗАДАЧА ОТ МУДРОЙ СОВЫ
166. Семь гномов собрали вместе 28 грибов. Все они собрали разное количество грибов, и ни у кого не оказалось пустой корзинки. Сколько грибов собрал каждый гном?
Сравнение натуральных чисел
Содержание
«Больше или меньше?» – этот вопрос будет преследовать нас повсюду каждый день. Давайте представим, что 2 одноклассника решили поспорить на 200 рублей.
Победителем спора будет тот, кто больше сделает самолётиков из бумаги. И вот, чтобы помочь выиграть, научимся сравнивать натуральные числа. Ведь именно так, посмотрев на результат соперника, можно увидеть, кто пока выигрывает.
Вспомним, что все натуральные числа образуют натуральный ряд чисел:
В этом натуральном ряду каждое следующее число на единицу больше, чем предыдущее. Или каждое следующее число получается прибавлением к предыдущему единицы.
Так, 4 на единицу больше, чем число 3. А если к 9 прибавить 1, получится следующее число – 10. И так с каждой парой соседних чисел в ряду натуральных чисел.
Из двух натуральных чисел больше то, которое в ряду натуральных чисел стоит правее (дальше от начала).
Это означает, что чем дальше от начала находится число в ряду натуральных чисел, тем оно больше.
Например, число 13 больше числа 9, число 9 больше числа 5, так как в ряду натуральных чисел число 13 находится правее числа 9, а 9 правее числа 5.
И наоборот, число 9 меньше числа 13, число 5 меньше числа 9, так как в ряду натуральных чисел, число 9 находится левее числа 13, а 5 левее числа 9.
Если одно число больше или меньше другого, то в математике это называется неравенством.
Но это лишь один из способов. Выделяют и другие. Например:
Одно число больше другого, если его при счёте произносишь позже, а меньше, соответственно, то, которое называешь раньше.
Знаки сравнения
Эти знаки похожи на открытый клюв птицы, которая хочет съесть как можно больше.
Двойное неравенство
С простым неравенством разобрались, но в математике выделяют ещё и двойное, то есть, когда сравнивают уже не 2, а 3 числа. Соответственно, в таком случае уже не 1 знак, а 2. Давайте разберёмся. Выделяют несколько особенностей, сравнивая 3 числа.
Сравнение многозначных чисел
Сравнить числа 9 и 13 легко, потому что числа небольшие и легко понять, какое из них будет находиться в ряду правее, и какое левее.
А если числа, которые нужно сравнить, большие, состоят из трех и более цифр? Такие как 648 и 7352, или 340567 и 341974. Каким образом выяснить, какое из чисел будет больше? Для этого нужно посмотреть, из скольких цифр состоят числа.
Из двух чисел больше то число, у которого цифр больше.
Рассмотрим еще один пример. Допустим, у нас есть числа 2, 876, 63, 20987, 7774, 109453. И нам нужно расположить их по возрастанию, то есть от самого маленького до самого большого. Обратим внимание, из скольких цифр состоит каждое число:
| Число | Сколько в нем цифр |
|---|---|
| 2 | 1 цифра |
| 876 | 3 цифры |
| 63 | 2 цифры |
| 20987 | 5 цифр |
| 7774 | 4 цифры |
| 108453 | 6 цифр |
Значит, самым маленьким будет число из одной цифры – это число 2. Далее будет число, состоящее из двух цифр – это число 63. Следующее состоит из трех цифр – число 876. Затем из пяти цифр – 20987. И самым большим будет число, которое состоит из 6 цифр – 108453.
Сравнение многозначных чисел с одинаковым количеством цифр
Чтобы сравнить 2 числа, можно сравнивать их по разрядам, начиная с наивысших.
Сравним 2305 и 2186.
Сравниваем по очереди тысячи, сотни, десятки и единицы обоих чисел. Итак, тысячи тут совпадают (и там 2, и там 2), тогда смотрим на сотни.
В 2305 – 3 сотни, а в 2186 – 1 сотня. Значит, в в 2305 больше сотен, чем в 2186, поэтому 2305 > 2186.
Из двух чисел с одинаковым количеством цифр, больше то, у которого больше первая (слева направо) из неодинаковых цифр
Сравним 4910 и 4909. Сравниваем цифры слева направо:
Для удобства запишем эти числа одно под другим:
Итак, первые слева цифры у чисел – это четвёрки. Значит, сравниваем следующие цифры. Далее идут девятки. Значит, сравниваем следующие. И так будем сравнивать до тех пор, пока сравниваемые цифры не будут разными.
Смотрим далее – у первого числа стоит 0, а у второго в этой позиции – 1. 1 больше, чем 0, значит, и второе число больше, чем первое.
493 0 978
493 1 423
Сравнение отрезков
Стоит отметить, что в математике сравнивают не только числа, но и буквы, а именно отрезки.
Например, PE – 5 см, KO – 5 см, а QM – 10 см.
Конечно, длиннее будет QM, то есть QM > PE.
Сравнение натуральных чисел
Урок 6. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Сравнение натуральных чисел»
Представим себе такую историю.
– Паша, а ты знаешь, что в созвездии Большой Медведицы больше звёзд, чем в созвездии Кассиопеи? – спросил Саша.
– Почему? – удивился Паша.
– Потому что в созвездии Большой Медведицы 7 звёзд, а в созвездии Кассиопеи всего лишь 5.
– Да, но это лишь видимые невооружённым глазом звёзды созвездий, – уточнил Паша. А на самом деле эти созвездия составляют гораздо больше звёзд.
Если ты посмотришь на эти созвездия в телескоп, то увидишь, что созвездие Большой Медведицы содержит около 200 звёзд, а созвездие Кассиопеи – около 150.
А на небе эти созвездия занимают огромную площадь. Так, например, площадь Большой Медведицы – 1280 квадратных градусов, а Кассиопеи – 598 квадратных градусов.
– Ого! Так много! – удивился Саша. – Только вот теперь я не могу понять, какое же из созвездий будет больше.
– Надо подумать! – сказал Паша. – А может не будем терять время и спросим у Электроши?
– Ребята, прежде чем я вам расскажу, как сравнивать большие числа, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим о сравнении. Что значит сравнить два числа?
– Наверное, это значит определить, какое из них больше, а какое – меньше, – предположили мальчишки.
– Правильно! – похвалил ребят Электроша. Когда Саша рассказывал, что созвездие Большой Медведицы состоит из 7 звёзд, а созвездие Кассиопеи – из 5, то ему не составило труда определить, что в первом созвездии больше звёзд, чем во втором. Понятно, что число 7 больше 5.
– Числа можно сравнивать при помощи натурального ряда, – сказал Электроша. – Что называют натуральным рядом?
– Все натуральные числа, записанные в порядке возрастания, образуют натуральный ряд, – ответил Паша.
– Молодец! – похвалил Пашу Электроша. – Запомните! Из двух натуральных чисел меньшим будет то, которое в натуральном ряду стоит раньше, а большим – то, которое в натуральном ряду стоит позже.
Вот, например, число 5 в натуральном ряду стоит раньше, чем число 7, поэтому мы и говорим, что 5 меньше 7.
Результаты сравнения записывают с помощью знаков «меньше» и «больше». А сами записи называют неравенствами.
1 — самое маленькое натуральное число. Число 0 меньше любого натурального числа. Значит, число 0 и меньше 1.
Кстати, сравнивать можно одновременно и три числа. Например, сравним числа 15, 10 и 20. Что вы можете сказать об этих числах относительно их расположения в натуральном ряду? – спросил у ребят Электроша.
– Число 15 в натуральном ряду стоит позже 10, значит, число 15 больше 10, – сказал Саша.
– Но ведь в то же время число 15 в натуральном ряду стоит раньше 20, значит, число 15 меньше 20, – перебил Паша.
– Верно! – подтвердил Электроша. – Если о числе говорят, что оно меньше некоторого числа и вместе с тем больше некоторого другого числа, то тогда это утверждение записывают в виде двойного неравенства, используя при этом и знак меньше, и знак больше. Зачастую слово «двойное» не говорят, а просто называют двойное неравенство неравенством.
– Сравнивать натуральные числа можно и при помощи координатного луча, – продолжил Электроша. – Давайте начертим луч Ох и отметим на нём точки А, В, С, D, Е в любом понравившемся вам месте.
А теперь представьте себе, что наш координатный луч – это изображение линейки, на которой отмечены указанные точки. Не зная координат этих точек, вы сможете сказать, какая из них больше, а какая меньше? – спросил у ребят Электроша.
– Да, – ответили мальчишки.
– Точка А стоит левее других точек на координатном луче, значит, её координата будет меньше, – сказал Паша.
– А точка Е стоит дальше других точек на координатном луче, тогда её координата будет больше, – продолжил Саша.
– Всё правильно! – похвалил ребят Электроша. – На координатном луче точка с меньшей координатой расположена левее точки с большей координатой.
Так, например, точка А с координатой 3 лежит левее точки B с координатой 7. Значит, координата точки А меньше координаты точки B.
Запомните! На координатном луче из двух натуральных чисел меньшее число расположено левее большего.
Но не все натуральные числа удобно сравнивать, обращаясь к натуральному ряду или координатному лучу. Возьмём, к примеру, многозначные числа 200 и 150, 1280 и 598. Чтобы сравнить эти числа, нам не очень удобно будет выписывать весь натуральный ряд или чертить такой большой координатный луч. Как сравнить такие числа?
– Может, попробовать сравнить по отдельности цифры каждого числа? – предложили мальчишки.
– Мне нравится ваше предположение, – сказал Электроша. – Проще всего сравнивать многозначные числа, которые имеют разное количество цифр. Вот, например, числа 1280 и 598. Первое число содержит 4 цифры – оно четырёхзначное, второе число содержит только 3 цифры – оно трёхзначное. Какое из них будет больше?
– Четырёхзначное число больше трёхзначного, – сказал Паша, – то есть число 1280 больше 598.
– Правильно! – сказал Электроша. – Запомните! Из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше.
Ну а если два многозначных числа имеют одинаковое количество цифр, то следует запомнить следующее правило: из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
– Сравните числа 200 и 150, – предложил ребятам Электроша.
– Числа 200 и 150 имеют одинаковое количество цифр, они оба трёхзначные, – сказал Паша, – но в первом числе в разряде сотен стоит цифра 2, а во втором – 1. 2 больше 1, значит, и число 200 больше 150.
– Всё правильно! – похвалил Пашу Электроша. Теперь зная, как сравнивают большие числа, вы можете сказать, какое из созвездий – Большая Медведица или Кассиопея – больше?
– Да! – воскликнули ребята. – Большая Медведица состоит из большего количества звёзд, а ещё она занимает и большую площадь на небе.
– Какие вы молодцы! – похвалил ребят Электроша. – А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
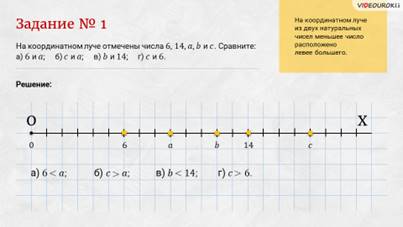
Задание первое: на координатном луче отмечены числа 6, 14, а, b и c. Сравните их.
Решение: мы знаем, что на координатном луче из двух натуральных чисел меньшее число расположено левее большего. Видим, что число 6 на координатном луче расположено левее числа а, значит, число 6 меньше а. Число с на координатном луче расположено правее числа а, значит, число с больше а. Число b на координатном луче расположено левее числа 14, значит, число b меньше 14. И последняя пара чисел. Видим, что на координатном луче число c расположено правее числа 6, значит, число c больше 6.
Следующее задание: сравните числа.
Решение: мы знаем, что из двух натуральных чисел меньшим будет то, которое в натуральном ряду стоит раньше, а большим – то, которое в натуральном ряду стоит позже. Число 4 в натуральном ряду стоит раньше числа 9, значит, 4 меньше 9.
Число 17 в натуральном ряду стоит позже 7, значит, 17 больше 7.
Следующая пара чисел: 106 и 160. Эти два числа имеют одинаковое количество цифр, они оба трёхзначные. Мы знаем, что из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр. В разряде сотен и у первого, и у второго числа стоит 1. Переходим к следующему разряду. Видим, что в разряде десятков в первом числе стоит 0, а во втором – 6. 0 меньше любого натурального числа, значит, и 0 меньше 6. Можем сделать вывод, что и всё число 106 меньше 160.
Сравним числа 975 и 957. Опять же видим, что эти числа имеют одинаковое количество цифр. В разряде сотен у обоих чисел стоит 9. Переходим к следующему разряду. Видим, что в разряде десятков, в первом числе, записана цифра 7, а во втором – 5. 7 больше 5. Значит, можем сделать вывод, что и всё число 975 больше числа 957.
Следующая пара чисел: 6 800 201 и 6 802 001. Оба числа семизначные, то есть имеют одинаковое количество цифр. В разряде единиц миллионов у этих чисел записана цифра 6. В следующем разряде сотен тысяч у них записана цифра 8. Переходим к следующему разряду. Видим, что в разряде десятков тысяч у обоих чисел записаны нули. А в разряде единиц тысяч в первом числе стоит цифра 0, а во втором – 2. 0 меньше 2. Значит, делаем вывод, что число 6 800 201 меньше числа 6 802 001.
И последняя пара чисел – 53 020 040 789 и 5 300 020 040 987. Видим, что эти числа состоят из разного количества цифр. Первое число одиннадцатизначное, второе – тринадцатизначное. А мы знаем, что из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше. В первом числе цифр меньше, значит, и всё число меньше.