Что значит соединить точки попарно 5 класс
Точка и линия
Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.
Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.
Зачем нужна точка, если она воображаемая? Для чего ее придумали?
Точка выполняет только одну задачу: указание месторасположения.
Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.
Линия – это множество точек, расположенных последовательно друг за другом.
Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.
Рис. 1 Цепь и линия
Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.
Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?
Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.
Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.
Рис. 2 Путь автомобиля
Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.
Рис. 3 Контур и диапазон
Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.
Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.
Обозначение точек и линий
Рис. 4 Обозначение точек и линий
Взаимное расположение точек и линии
Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.
Рис. 4.1 Принадлежность точек линии
При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H
Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:
Виды линий
Рис. 5 Замкнутая и незамкнутая линия
Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.
Рис. 6 Контур птицы
Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).
Рис. 7 Незамкнутые линии
Еще несколько примеров.
1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.
2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
Также линии бывают:
Рис. 11 Самопересекающиеся и не самопересекающиеся линии
Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.
Рис. 12 Прямая, ломаная, кривая линии
Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.
Мерзляк 5 класс — § 3. Отрезок. Длина отрезка
Вопросы к параграфу
Решаем устно
1. Реши:
2. Назовите все двузначные числа, сумма цифр которых равна 6.
3. Назовите все двузначные числа, разность цифр которых равна 7.
4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырёхзначное число.
9 999, 10 000, 10 001
5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырёхзначное число.
6. Выразите в сантиметрах:
7. Выразите в дециметрах и сантиметрах:
Упражнения
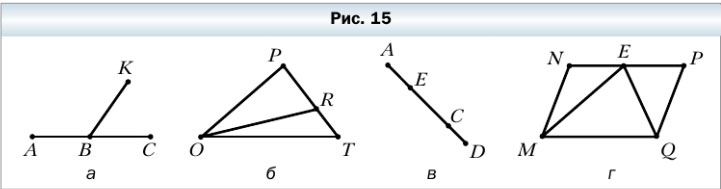
44. Запишите все отрезки, изображённые на рисунке 15.
б) OP, PR, RT, PT, TO, OR
в) AE, AC, AD, EC, ED, CD
г) MN, NE, NP, EP, PQ, QE, QM, EM
45. Запишите все отрезки, изображённые на рисунке 16.
а) BO, BD, OD, CO, CA, OA, AD
б) FK, FE, KE, EN, ES, NS, MK, MN, MP, KN, KP, NP
46. Отметьте в тетради точки А, В, С, D и соедините их попарно отрезками. Сколько отрезков образовалось? Сколько образовалось отрезков с концом в точке A?
Комментарий: новую точку на чертеже, образованную пересечением отрезков AC и BD мы не учитываем, поскольку о ней не говорится в задании.
Для того, чтобы образование 6 отрезков выглядело более наглядно, можно расположить заданные точки в следующем порядке:
Такое решение задания также является правильным.
47. Начертите отрезки MN и АС так, чтобы MN = 6 см 3 мм, АС = 5 см 4 мм.

48. Начертите отрезки EF и ВК так, чтобы EF = 9 см 2 мм, ВК = 7 см 6 мм.
49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрезка АС?
50. Начертите отрезок ТР, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?
TP — TE = 7 см 8 мм — 2 см 6 мм = 5 см 2 мм
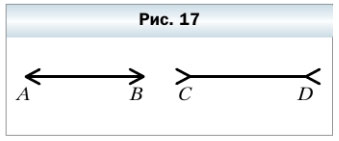
51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.
Глядя на рисунок 17 кажется, что отрезок CD > AB.
Проверим вывод измерением:
Ответ: эти отрезки равны.
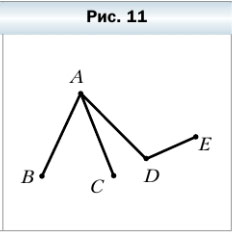
52. Назовите все ломаные, изображённые на рисунке 11. Какая из них имеет наибольшее количество звеньев?
На рисунке 11 можно выделить 5 ломаных:
Значит наибольшее количество звеньев имеют ломанные BADE и CADE.
53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
Назовём звенья ломанной и измерим их длину:
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
AB + BE + EK + KP + PR = 19 + 18 + 16 + 11 + 12 = 76 (мм) — длина ломаной ABEKPR
Ответ: длина ломаной 76 мм.
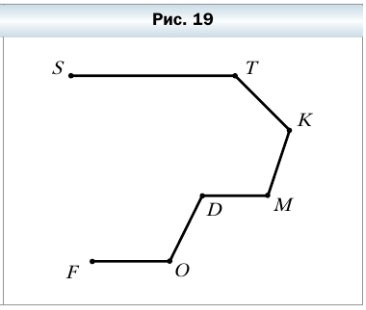
54. Запишите звенья ломаной, изображённой на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
Назовём звенья ломанной и измерим их длину:
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
ST + TK + KM + MD + DO + OF = 27 + 13 + 11 + 11 + 12 + 13= 87 (мм) — длина ломаной STKMDOF
55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клетки правее и на 1 клетку выше точки В; точку D — на 3 клетки правее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки А, В, С, D и Е. Какая фигура образовалась? Запишите её название и укажите количество звеньев.
Образовалась фигура ломаная ABCDE. Она состоит из 4 звеньев.
56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
AB + BC + CD + DE = 8 + 14 + 23 + 10 = 55 (см) — длина ломаной ABCDE.
Ответ: длина ломаной 55 см.
57. Вычислите длину ломаной MNKPEF, если MN= 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.
Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:
MN + NK + KP + PE + EF = 42 + 38 + 19 + 12 + 29 = 140 (мм) — длина ломаной MNKPEF.
Ответ: длина ломаной 55 см.
58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.
Измерим длины звеньев ломаной:
AB + BC + CD = 18 + 30 + 36 = 84 (мм) — длина ломаной ABCD
Ответ: длина ломаной 84 мм.
59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.
34 • 3 = 102 (см) — длина отрезка SK.
34 + 102 = 136 (см) — длина отрезка RK.
Ответ: длина отрезка RK 136 см.
60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если AD = 135 см.
135 : 5 = 27 (см) — длина отрезка DB.
135 + 27 = 162 (см) — длина отрезка АВ.
Ответ: длина отрезка АВ 162 см.
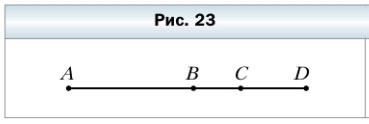
61. Известно, что АС = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.
32 — 9 = 23 (см) — длина отрезка AB.
9 + 12 = 21 (см) — длина отрезка BD.
Ответ: AB = 23 см, BD = 21 см.
62. Известно, что MF= 43 см, ME = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.
26 — 18 = 8 (см) — длина отрезка MK.
43 — 26 = 17 (см) — длина отрезка EF.
Ответ: MK = 8 см, EF = 17 см.
63. Даны две точки А и В. Сколько можно провести отрезков, соединяющих эти точки? Сколько можно провести ломаных, соединяющих эти точки?
64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.
На рисунке образовались отрезки: MA, MC, MK, AC, AK, CK. Всего 6 отрезков.
65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому отрезку, причём точка К лежит между точками М и В, AM = 12 см, ВК = 9 см. Найдите длину отрезка МК.
28 — (12 + 9) = 28 — 21 = 7 (см) — длина отрезка MK.
66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрезка ВС? Есть ли в условии задачи лишние данные?
Так как по условию задачи АВ на 5 см больше отрезка АС, то есть AB — AC = 5 см, то BC = 5 см.
Фраза «длина отрезка АС равна 15 см» является лишней в условии задачи, поскольку длина отрезка BC будет равна 5 см независимо от значения длины отрезка АС.
Ответ: 5 см, да «длина отрезка АС равна 15 см» — лишние данные.
67. Отрезки MT и FK равны (рис. 25). Сравните отрезки MF и ТК.
По условию MT = FK. Значит можно записать уравнение:
68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.
15 + 24 + 32 = 71 (мм) — длина ломаной ACDM.
69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.
8 + 22 + 15 = 45 (мм) — длина ломаной CEFK.
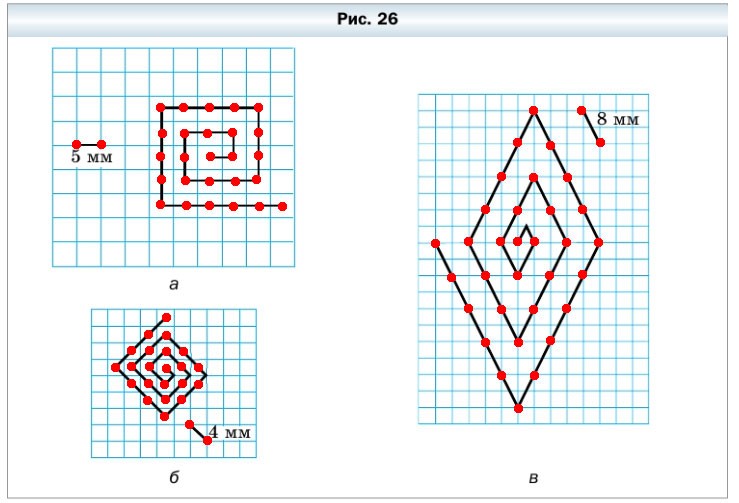
70. Вычислите длину ломаной, изображённой на рисунке 26.
Разделим ломаные на единичные отрезки равные заданному и посчитаем их количество.
Ответ: 125 мм, 84 мм и 248 мм.
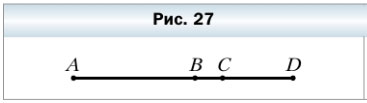
71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.
8 — 2 = 6 (см) — длина отрезка AB.
6 + 6 = 12 (см) — длина отрезка AD.
72. Известно, что MF= 30 см, ME = 18 см, KF = 22 см (рис. 28). Найдите длину отрезка КЕ.
30 — 18 = 12 (см) — длина отрезка EF.
22 — 12 = 10 (см) — длина отрезка KE.
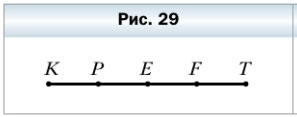
73. Известно, что KP = PE = EF= FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.
На рисунке 29 можно найти следующие равные отрезки:
74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?
Это значит, что расстояние между крайними точками у первого и второго отрезка будет одинаковым.
Проверим вывод графически:
75. Известно, что АЕ = 12 см, AQ = QB, ВМ = MС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.
Для удобства обозначим равные отрезки отдельными цветами.
1) Известно, что МК = 4 см.
ВМ + KD = MС + СК = 4 см
3) ВD = ВМ + MС + KD + СК = ( ВМ + KD) + ( MС + СК) = 4 + 4 = 8 см
4) Мы знаем, что АЕ = 12 см, ВD = 8 см.
AQ + QB + DR + RE = АЕ — ВD = 12 — 8 = 4 см
AQ + RE = QB + DR = 4 : 2 = 2 см
6) QR = АЕ — ( AQ + RE ) = 12 — 2 = 10 см
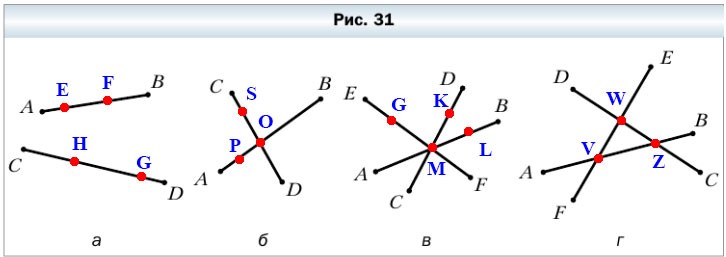
76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них были две отмеченные точки, не считая концов отрезков?
а) Надо отметить 4 точки: две на отрезке AB (например E и F) и две на отрезке CD (например H и G).
б) Надо отметить 3 точки: точку пересечения отрезков CD и AB (точка O) и по одной точке на отрезке CD (например точку S) и на отрезке AB (например P).
в) Надо отметить 4 точки: точку пересечения отрезков EF, AB и CD (точка M), а также по одной точке на отрезке EF (например G), отрезке AB (например точку L) и отрезке CD (например K).
г) Надо отметить 3 точки: точку пересечения отрезков DC и FE (точка W), точку пересечения отрезков AB и FE (точка V) и точку пересечения отрезков AB и DC (точка Z).
77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может построить отрезок длиной:
1) 3 см — Миша должен начертить отрезок 13 см, а потом от одной из конечных точек два раза отмерить по 5 см:
13 — 5 • 2 = 13 — 10 = 3 (см)
2) 2 см — Миша должен три раза отмерить отрезки по 5 см, а потом вычесть из полученного большого отрезка отрезок 13 см:
5 • 3 — 13 = 15 — 13 = 2 (см)
3) 1 см — Миша должен два раза отмерить отрезки по 13 см, а потом из полученного большого отрезка вычесть пять раз по 5 см:
13 • 2 — 5 • 5 = 26 — 25 = 1 (см)
Упражнения для повторения
78. Вычислите:
79. Выполните действия:
80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограммов больше подарили конфет, чем печенья?
1) 5 • 4 = 20 (кг) — конфет подарили.
2) 3 • 6 = 18 (кг) — печенья подарили.
3) 20 — 18 = 2 (кг) — конфет больше, чем печенья.
Ответ: конфет подарили больше на 2 кг.
81. Медведица Настасья Петровна заготовила на зиму 7 бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасья Петровна?
1) 12 • 7 = 84 (кг) — мёда в 12-ти килограммовых бочонках.
2) 10 • 8 = 80 (кг) — мёда в 10-ти килограммовых бочонках.
3) 84 + 80 = 164 (кг) — мёда заготовила Настасья Петровна.
82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть привезённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

1) 240 + 156 = 396 (кг) — фруктов завезли.
2) 396 : 3 = 132 (кг) — фруктов продали в 1 день.
3) 396 — 132 = 264 (кг) — фруктов продали во 2 день.
83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского сада, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?
1) 246 + 354 = 600 (кг) — фруктов вырастил Кот Матроскин.
2) 600 : 6 = 100 (кг) — фруктов отдал в детский сад.
3) 600 : 5 = 120 (кг) — фруктов отдал в школу.
4) 600 — (100 + 120) = 600 — 220 = 380 (кг) — фруктов отдал в больницу.
Задача от мудрой совы
84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.
Для того, чтобы в искомом натуральном числе было наименьшее количество цифр найдём максимальное количество цифр 9 (самая большая цифра), которые мы сможем использовать:
99 : 9 = 11 — девяток можно использовать.
Далее найдём оставшуюся цифру, необходимую для того, чтобы сумма цифр искомого числа равнялась 101:
101 — 9 • 11 = 101 — 99 = 2 — оставшаяся цифра искомого числа.
Это значит, что в искомом натуральном числе одна цифра 2 и одиннадцать цифр 9. Теперь расположим цифры так, чтобы натуральное число было наименьшим.
299 999 999 999 — на место сотен миллиардов поставим самую маленькую цифру.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии