Что значит симметричные фигуры 2 класс
«Эти симметричные фигуры» (2 класс)
Описание презентации по отдельным слайдам:
Урок по математике на тему: «Эти симметричные фигуры…» Подготовлен и проведен учителем начальных классов Фалюта Л.В. во 2«А» классе
Ну-ка, проверь, дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка?
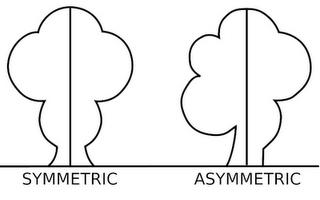
Запомните: фигурки, у которых одна половинка как две капли похожа на другую, называют зеркальной симметрией. (ОСЕВОЙ)
Эти фигуры называют симметричными относительно прямой линии, а прямую линию называют осью симметрии.
Достройте вторую половинку нашей работы.
Симметричен человек И увидеть можно: Глаза два и уха два. И руки две- точно! Две ноги и две ноздри, Щечки улыбаются. Симметричен человек, Это всех касается!
Издревле люди стремились украсить все, что окружало их в быту. Они старались простой предмет сделать нарядным, внести праздничность в повседневную жизнь. Украшали дома и ворота, столы и сундуки, орудия труда, посуду и многое другое.
Природа вдохновила человека на создание симметричных форм. Они придумывали удивительные замысловатые орнаменты. В построении орнамента часто используется симметрия. Сегодня на уроке мы будем учиться создавать орнаменты из геометрических фигур с помощью симметрии. СУРПАН- головная повязка
Орнамент – это узор, элементы которого подчинены определенному ритму
Красный – свобода Желтый – цвет солнца Белый – чистота помыслов, честь, благородство
Симметрия – порядок, четкость в изображении
Симметрия – способ создания красоты
Симметрия – способ создания совершенства
Симметрия! Я гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, ты в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза.
Выставка работ учащихся.
http://nikolaeva.21204s01.edusite.ru/p8aa1.html чувашская вышивка http://silova.21411s16.edusite.ru/p26aa1.html чувашская вышивка http://www.bestreferat.ru/referat-113224.html чувашские узоры http://artmus.culture21.ru/ppage.aspx?objid=23031&page=943&type=14&auth=1137&norole=1 чувашский орнамент www.chuvbook.ru учебник чувашского языка, рабочая тетрадь для 2 класс Картинки-раскраски
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-674766
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
В Хабаровском крае введут уроки по вакцинации в некоторых школах и колледжах
Время чтения: 1 минута
Дума приняла закон о бесплатном проживании одаренных детей в интернатах при вузах
Время чтения: 1 минута
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
«Урок с использованием ИКТ» во 2-м классе по теме «Симметрия»
Тема урока: «Симметрия».
Тип урока: урок с применение ИКТ.
Вид: комбинированный.
План урока:
| Содержание этапов урока | Виды и формы работы |
| 1. Организационный момент | Приветствие |
| 2. Мотивационное начало урока | Постановка цели урока |
| 3. Объяснение темы урока | Использование опорного конспекта и презентации |
| 4. Этап обобщения, систематизации знаний и закрепление изученного | Работа в печатных тетрадях, выполнение заданий |
| 5. Практическая работа на ПК | Работа с программой, задание: «Дорисуй платок» |
| 6. Подведение итогов, домашнее задание | Нарисовать домик, симметричный относительно вертикальной оси, на отдельном тетрадном листочке в клеточку. |
I. Организационный момент
II. Мотивационное начало урока
Учитель: Здравствуйте! Тема нашего сегодняшнего урока: «Симметрия».
Цель нашего урока – выяснить, что такое симметрия, где в жизни мы с ней встречаемся?
Для достижения цели нашего урока мы воспользуемся рисунками, которые лежат на ваших столах в конвертиках, такие же рисунки мы рассмотрим на экране (Приложение 1)
– Посмотрите на геометрические фигуры, назовите их.
– Возьмите первую фигуру и согните её пополам. Точно так же согните все фигуры.
– А теперь разверните рисунки, у вас получились две одинаковые фигуры, которые разделяет линия сгиба.
– Линия сгиба, называется осью симметрии.
Игра «Зеркало»
Учитель предлагает ученикам встать и стать его зеркалом, т.е. повторять все его движения в зеркальном отражении. Учитель поднимает руку – ученики тоже, отставляет ногу в сторону – ученики тоже. Однако нужно напомнить ученикам, что они – зеркало, т.е. они должны отражать все движения учителя. Возможно, дети поднимут вместе с правой рукой учителя свою правую руку (как на физкультуре), но, отражаясь в зеркале, правая рука становится левой. А если приблизиться к зеркалу вплотную, то можно слиться со своим отражением. Для демонстрации этого можно поставить перед собой какого-либо ученика, а затем медленно поднимать вверх свою правую руку, держа его левую. После этого провести еще ряд упражнений.
Теперь мы знаем, что в зеркале все становится наоборот: правая рука станет левой, левая нога – правой.
III. Объяснение нового материала
Учитель: Посмотрите теперь все на экран.
– Это предметы окружающей нас среды, назовите, что вы видите? (Слайд 2)
(Дети называют предметы)
– А теперь внимательно посмотрите на бабочку, крылья у бабочки одинаковые,
т.е. симметричные. назовите ещё симметричные предметы. (Слайды 2, 3)
– Из конверта возьмите рисунок 1 (Слайд 4) и раскрасьте симметричные предметы.
Учитель: Теперь давайте выполним задание 44 из тетради (Слайд 5) Представим себе, что на линию АБ поставили зеркало. Что мы увидим в этом зеркале? (Отражение этих предметов.) А как изменятся в этом зеркале предметы? (Будет все наоборот: то, что было правым – станет левым и наоборот.) Говорят, что эти отражения симметричны самим предметам.
После этого дети находят пары симметричных фигур: кораблики и варежки. А домики и уточки не будут симметричны.
Это можно проверить, если сложить лист по линии АБ. В этом случае предметы должны совпасть. Такие предметы называются симметричными относительно оси АБ.
IV. Этап обобщения, систематизации знаний и закрепление изученного
Учитель: А теперь мы будем учиться строить фигуры, которые симметричны данным относительно заданной оси. (Cлайд 6)
а) Далее, учитель объясняет детям, как получить точку, симметричную данной относительно заданной оси: нужно отступить от оси направо на столько же клеточек, на сколько отстоит исходная точка.
Аналогично нужно получить концы отрезка, или вершины треугольника, или точки, ограничивающие и определяющие флажок. Затем полученные точки нужно соединить по линейке и образовать искомые фигуры. И, чтобы убедиться в их симметричности относительно данным фигурам, – сложить лист по прямой АБ.
Учитель: Эта прямая называется вертикальной осью симметрии, а теперь попробуем нарисовать фигуры, симметричные относительно горизонтальной оси.
– Показывая разные фигуры и предметы (квадрат, треугольник, домик, солнышко и т.д.) учитель спрашивает ребят наличие или отсутствие осей симметрии.
К доске вызываются три ученика, с каждого ряда по одному ученику, и работают у доски с рисунками (дерево, груша и стрекоза), т.е. проводят оси симметрии у предметов, остальные ребята на местах выполняют задание (рисунок 3) из конверта.
Задание 47 выполняется в тетради самостоятельно (Cлайд 7)
Физкультминутка
На раз — всем дружненько присесть.
На два — подняться — руки вверх.
На три — носки свои достать.
И за парты сесть опять.
– Ну вот мы уже хорошо научились рисовать, поэтому возьмите из конверта заготовки рисунка «львёнка», дорисуйте по клеткам и раскрасьте его так, чтобы он был симметричным не только по форме, но и по цвету.
Загадки, задачи-шутки
1) Мудрец в нем видел мудреца,
Глупец – глупца,
Баран – барана,
Овцу в нем видела овца,
И обезьяну – обезьяна,
Но вот подвели к нему Федю Баратова,
И Федя увидел неряху лохматого. (Зеркало.)
2) Два конца, два кольца, а посередине – гвоздик. (Ножницы.)
А есть ось симметрии? (Да. В случае непонимания – показать ножницы, но симметричные, или изобразить на доске.)
3) Между двух светил я в середине один. (Нос.)
А есть ли ось симметрии? (Да.)
4) Какие буквы имеют оси симметрии? (Слайд 11)
(А, В, Д, Е, Ж, 3, К, Л, М, Н, О, П, С, Т, Ф, X, Ш, Э, при этом имеется в виду их симметричное написание. Выписать их на доске.)
Какие из них имеют несколько осей симметрии? (Ж – 2 оси, Н –2 оси, О – много, X– 2 оси.)
V. Практическая работа на ПК
Программа дорисуй платок относительно оси.
VI. Домашнее задание.
а) Нарисовать домик, симметричный относительно вертикальной оси, на отдельном тетрадном листочке в клеточку.
б) Принести два тетрадных листочка.
Внеурочное занятие по логике на тему «Симметрия» (2 класс)
Внеурочная деятельность. Кружок «Логика».
Тема. Симметрия. Симметричные фигуры.
Цель: ввести понятие «симметрия». Учить строить симметричные фигуры. Ввести понятие оси симметрии. Научить находить ось симметрии некоторых фигур.
1 Создать условия для развития у детей познавательных интересов, формирование стремления ребенка к размышлению и поиску.
Обеспечить становление у детей развитых форм сознания и самосознания.
Обучить приемам поисковой и творческой деятельности.
Развитие комплекса свойств личности, которые входят в понятие «творческие способности».
учиться объяснять свое несогласие и пытаться договориться;
учиться выражать свои мысли, аргументировать;
учиться выполнять различные роли в группе (лидера, исполнителя);
развивать доброжелательность и отзывчивость;
развивать способность вступать в общение с целью быть понятым.
Предметными результатами являются формирование следующих умений:
применять правила сравнения;
находить закономерность в числах, фигурах и словах;
строить причинно-следственные цепочки;
находить ошибки в построении определений;
Основные методы и технологии развития УУД
— организация учебного сотрудничества в парах и группе
— игровые технологии в форме упражнений
— Сегодня наше занятие я предлагаю начать с загадки.
Мудрец в нём видел мудреца,
Овцу в нём видела овца,
И обезьяну – обезьяна
Но вот подвели к нему Федю Баратова,
И Федя увидел неряху лохматого. (Зеркало)
— Ежедневно каждый из нас по несколько раз видит своё отражение в зеркале. Это настолько обычно, что мы не удивляемся, не задаём вопросов, не делаем открытий.
— Перед вами лежат листы с изображением. Приложите к каждому изображению по пунктирной линии зеркало, что мы увидели? Но ведь буквы не были написаны полностью, как вы определили, что там написаны именно эти буквы? Лист 1 (раздаточный материал) (Вторую половину мы увидели в зеркале)
— В переводе слово «симметрия» означает «соразмерность в расположении частей чего-либо или строгая правильность»
— Посмотрите на снежинку, бабочку, листок. Их объединяет то, что они симметричны.
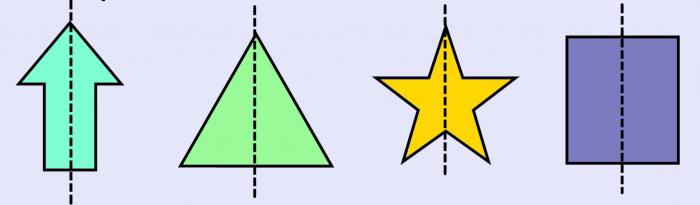
— Возьмите лист 2. Рассмотрите фигуры, приставляя зеркало к пунктирным прямым линиям.
— Что вы заметили? (в зеркале отражается вторая часть фигуры)
— А теперь вырежьте их и сложите по прямым линиям. Сделайте вывод.
— Прямая, по которой вы сложили фигуры, называется осью симметрии. Если симметричную фигуру сложить по оси симметрии, то половины фигуры совпадут.
— Как расположены пунктирные линии? (вертикально и горизонтально)
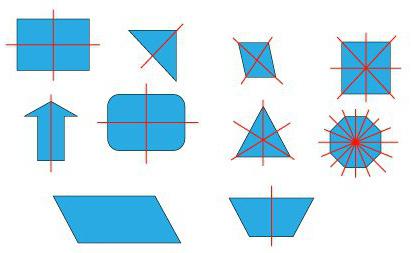
Задание «Сколько осей симметрии?»
— Когда вы складывали фигуры, что вы заметили? (Что некоторые фигуры можно было сложить несколько раз).
— О чём это говорит.? Что у некоторых фигур может быть несколько осей симметрии.
— Сколько осей симметрии у квадрата (4), у равностороннего треугольника (3), у прямоугольника (2 ), у круга (бесконечно много), у овала (2)
— Встали. Я предлагаю вас стать моим зеркалом. ( поднять руку, отставить ногу, присесть, шагнуть вперёд и т.д.)
(В зеркале «всё наоборот» правая рука становится левой. Значит, если флажок «смотрит» направо, в зеркале он должен «смотреть» …)
Групповая работа (5 мин)
Задание «Составь симметричные пары»
— На партах лежат конверты с фигурами и лист 3.
— Изменилась ли в «зеркале» данная фигура?»
1. Два конца, два кольца, а посередине – гвоздик. (ножницы)
-Есть ось симметрии? 9Да)
2. Между двух светил я в середине один. (Нос). А есть ли ось симметрии? (да)
3. Отгадайте-ка, ребятки,
Что за цифра – акробатка?
Если на голову встанет,
Ровно на три больше станет. (Шесть)
-Относительно какой оси отразили эту цифру? Горизонтальной
4. Оля стоит перед зеркалом и причёсывается правой рукой. Какой рукой причёсывается её отражение? (левой)
Технология. 2 класс
Конспект урока
Технология. 2 класс
Урок № 3 «Что такое симметрия?»
Ключевые слова: Симметрия, композиция, ось симметрии
Открытые электронные ресурсы по теме урока: Сайт центра технологического образования АО Издательство «Просвещение» (http://technology.prosv.ru)
Теоретический материал для самостоятельного изучения:
И в искусстве, и в природе присутствуют такие понятия, как симметрия и асимметрия. Их мы наблюдаем повседневно в окружающем нас мире. И каждому субъекту присущи одно из или оба этих понятия.
Симметрия – это соразмерность, пропорциональность, одинаковость в расположении частей.
Симметрией обладают не только геометрические фигуры или вещи, сделанные рукой человека, но и многие творения природы (бабочки, стрекозы, листья, морские звезды, снежинки). Особенно разнообразны свойства симметрии кристаллов. Одни из них более симметричны, другие — менее.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии».
Воображаемая линия сгиба в симметричных изображениях называется осью симметрии.
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три: Зеркальная – наблюдается относительно одной или нескольких плоскостей. Также термин употребляется для обозначения типа симметрии, когда используется такое преобразование, как отражение.
Лучевая, радиальная или осевая, в общем смысле – симметрия относительно прямой. Может рассматриваться как частный случай вращательной разновидности.
Центральная – наблюдается симметричность относительно некой точки.
Художественное вырезание из бумаги – уникальный вид искусства. Существует два метода вырезания — ножницами и ножом. В разных странах искусство вырезания называется примерно одинаково, в переводах — как «бумажная картинка», «бумажный цветок», «вырезка из бумаги», «вырезка ножницами», «силуэтное вырезание», «вытынанка» и т. д. Современные работы, выполненные в технике художественного вырезания из бумаги, называют прорезными изображениями, бумажной графикой, ажурным (филигранным) вырезанием. В этой технике можно делать много красивых вещей: картины (панно), открытки, украшения на окна и многое другое.
Одним из интересных, но сложных по технике выполнения является симметричное вырезание.
Симметричное вырезание заключается в том, что у изображаемого предмета одна часть симметрична другой, воображаемая плоскость делит предмет пополам, на две одинаковые зеркальные половины (лист дерева, само дерево, цветок тюльпана или василька, ваза, бокал, человек и т.п.).
Наиболее простыми для передачи в аппликации являются листья. Большинство из них построено по принципу зеркальной симметрии. Несмотря на многообразие формы листовой пластины (простые, простые рассеченные, сложные), различие по протяженности, относительной величине, строению краев, по окраске, все они (кроме неравнобоких) характеризуются общим распределением боковых сторон равномерно справа и слева.
Поэтому при вырезании листьев целесообразно применять прием предварительного складывания заготовок пополам (для передачи в аппликации зеркального соответствия боковых сторон) и одновременного прорезания обоих слоев бумаги по воображаемому контуру половины фигуры относительно сгиба. Изменение формы заготовки, ее соотношения по ширине и длине, величине и окраске позволяет изобразить многообразие и многоцветие листьев, особенно осенних.
При вырезании листьев путем сгибания заготовки пополам следует учитывать особенности строения исходной фигуры, соотношение ее величины и формы. Квадратная бумага необходима для изображения сердцевидных листьев (сирень). Длинные полоски нужны при вырезании линейных форм, например, листьев нарцисса, амариллиса, ириса. Яйцевидные листья получают из прямоугольной заготовки, у которой отношение ширины к длине не имеет резкого различия (например 6х4 см).
Для вырезания цветков из бумаги можно применить описанный выше прием складывания заготовки пополам, чтобы отобразить в аппликации равенство противоположных частей симметричной фигуры. После складывания бумаги вырезают половину формы цветка. При этом изменение очертаний контура, окраски и величины бумажной заготовки позволяет получить различные изображения колокольчиков, ландышей, ирисов, лилий.
Из заготовки бумаги, разделенной путем сложения на двенадцать равных частей, также можно вырезать разнообразные формы снежинок.
Сегодня на уроке вы познакомились с таким понятием как симметрия, с видами симметрии и таким видом техники, как симметричное вырезание.
Разбор типового тренировочного задания
Впишите в текст пропущенное слово.
Соразмерность, пропорциональность, одинаковость в расположении частей – это …
Пропущенное слово – симметрия.
Выберите из списка правильный ответ.
Воображаемая линия сгиба в симметричных изображениях называется ….
Что такое симметрия и асимметрия?
Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?
Что означает симметрия в разных науках?
Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.
Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.
Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.
Как определяют симметрию разные словари?
На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.
В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.
Когда говорят об асимметрии?
Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.
В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.
О центральной и осевой симметрии
В математике выделяют такие ее виды:
Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.
В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.
Какие фигуры являются симметричными?
Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.
Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.
Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.
Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.
К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.
Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.
У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.
Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.
Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.