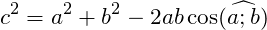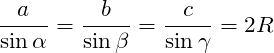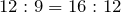Что значит решить треугольник в геометрии
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
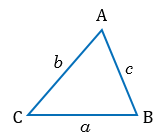
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Решение треугольника по двум сторонам и углу между ними
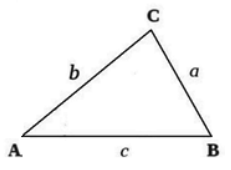
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
   . . |
Из формулы (3) найдем cosA:
  |
Поскольку уже нам известны два угла то находим третий:
  . . |
Решение треугольника по стороне и любым двум углам
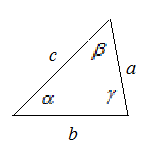
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Решение треугольников
Введем обозначения для сторон 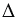
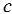
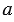
Далее рассмотрим задачи на решение треугольников с использованием данных обозначений.
Задача 1
| Решение треугольника по двум сторонам и углу между ними. |
Дано: 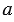
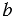

Найти: 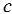


Решение:
1. По теореме косинусов: 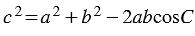

2. По теореме косинусов: 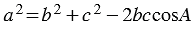

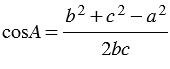
Задача 2
| Решение треугольника по стороне и прилежащим к ней углам. |
Дано: 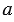


Найти: 
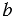
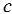
Решение:
2. По теореме синусов: 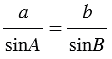
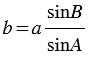
3. По теореме синусов: 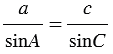

Задача 3
| Решение треугольника по трем сторонам. |
Дано: 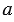
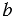
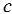
Найти: 


Решение:
1. По теореме косинусов: 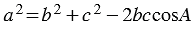

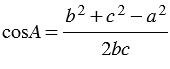
2. По теореме косинусов: 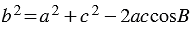
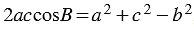
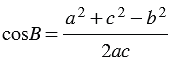
Пример
Стороны АВ, ВС и АС треугольника АВС соответственно равны 20 м, 14 м и 18 м. Определите значение угла А.
Решение:
По условию задачи 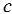
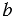
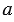
Следовательно, мы можем решить данный треугольник по трем сторонам (см. задачу 3), значит, найти угол А.
По теореме косинусов: 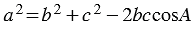

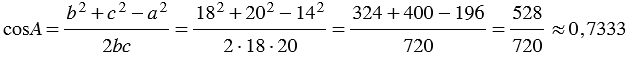
По таблице Брадиса находим угол А: 
Поделись с друзьями в социальных сетях:
Решение треугольников
Вы будете перенаправлены на Автор24
Предварительные сведения
Рисунок 1. Треугольник
Примеры задач на решение треугольников
Из определения мы видим, что если в треугольнике даны три каких-либо элемента треугольника, то его можно разрешить, то есть найти остальные три элемента этого треугольника. Будем рассматривать решение треугольника на примерах задач.
Решение.
Найдем сначала третью сторону по теореме косинусов:
Используя вновь теорему косинусов, имеем:
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle B=<180>^0-\angle A-\angle C\]
\[\angle A=arc\ cos\left(\frac
Решение.
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle A=<180>^0-\angle B-\angle C\]
По теореме синусов, имеем:
Готовые работы на аналогичную тему
Решение.
Найдем сначала один из углов по теореме косинусов:
Используя вновь теорему косинусов, имеем:
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle B=<180>^0-\angle A-\angle C\]
\[\angle A=arc\ cos\left(\frac
Решение.
По теореме синусов, имеем
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle C=<180>^0-\angle B-\angle A\]
По теореме косинусов, имеем:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 11 04 2021
Треугольник
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
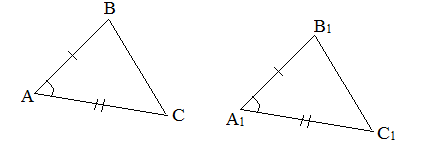
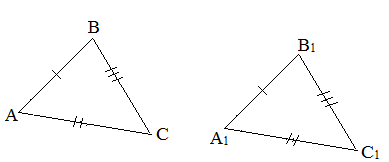
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
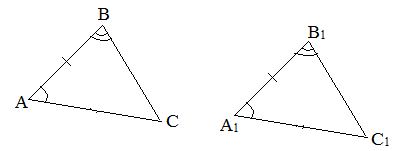
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
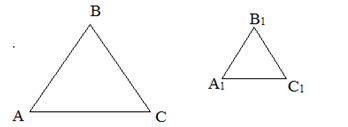
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
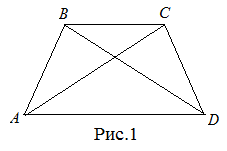
| Задание | Доказать, что в равнобокой трапеции диагонали равны. |
| Доказательство | В равнобокой трапеции 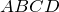 рассмотрим треугольники рассмотрим треугольники 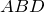 и и 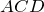 (рис. 1). Так как (рис. 1). Так как 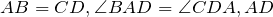 – общая сторона, то треугольники – общая сторона, то треугольники 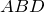 и и 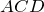 равны по первому признаку, а значит, равны все их элементы, т.е. равны по первому признаку, а значит, равны все их элементы, т.е. 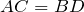 . . |
Что и требовалось доказать.
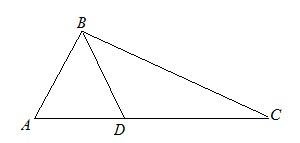
| Задание | В треугольнике 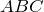 стороны стороны 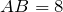 см см 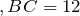 см см 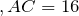 см. На стороне см. На стороне 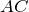 отмечена точка отмечена точка 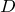 так, чтобы так, чтобы 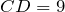 см. Найти отрезок см. Найти отрезок 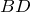 . . |
| Решение | Рассмотрим треугольники 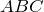 и и 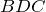 . Запишем отношение сторон . Запишем отношение сторон 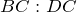 и и 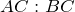 : : |
Так как выполняется равенство отношений, то соответствующие стороны треугольников пропорциональны, а также 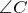
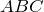
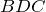
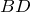
откуда 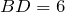
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.