Что значит решить обратную геодезическую задачу
Что такое обратная и прямая геодезическая задача: суть, методы решения, назначение
В строительстве большую часть времени занимают геодезические работы. Это комплекс различных измерений и вычислений на местности. Стоит ли говорить, что качество выполненных работ зависит от точности полученных результатов. Это влияет на размещение зданий и сооружений, а также возведение их конструктивных элементов. Все должно соответствовать проектным показателям и техническим регламентам. Геодезические работы выполняются в объеме, определенном особенностями объекта и стадией его реализации. Компания «Промтерра» специализируется на их проведении с составлением необходимых чертежей, схем и расчетов. Для этого есть все составляющие: действующая лицензия, опыт, допуск СРО, штат специалистов. Один из вопросов, который поступает при выполнении работ, касается геодезической задачи. Что это такое, как используется в работе и ее назначение.
Математика в действии
По своей сути геодезические задачи — это математика в чистом виде. Основная задача состоит в определении взаимного положения точек принадлежащих какой-либо поверхности. Наиболее часто приходится иметь дело с прямыми и обратными геодезическими задачами, но на этом математические вычисления не заканчиваются. В зависимости от поставленных условий могут применяться и другие виды. Например, решение треугольника по измеренным углам и сторонам. Интересный исторический факт: с геодезическими задачами исследователи этой темы работают уже больше трех веков, а споры относительно методов дальше продолжаются.
Что такое прямая геодезическая задача
Эта разновидность предполагает вычисление координат, то есть широты и долготы определенной точки. А она, в свою очередь, лежит на математически правильной поверхности — земном эллипсоиде. Вычисления производятся по координатам другой точки, по длине и азимуту геодезической линии. Точность решения зависит от корректности исходных данных. Для проведения вычислений используют формулы нахождения приращений и определения координат.
Специалисты применяют разные методы для получения результатов. Наиболее востребованными считаются косвенный и прямой. Они отличаются тем, что в основе лежит точность исходных данных. Косвенные методы решения очень чувствительны к ним. Если в исходнике есть значительные расстояния, изменения по азимуту, то вычисления не получится сделать, или они будут с большими погрешностями. Прямые методы работают по соотношениям сфероидической геодезии, поэтому результаты можно получить более точные. Кстати, прямой тип геодезических задач применяется при вычислении координат в теодолитном ходе.
Что такое ОГЗ: суть обратной геодезической задачи
При работе над обратной геодезической задачей вычисления проводятся по известным координатам двух точек на земном эллипсоиде. Это нужно для получения значений горизонтального положения линий между ними, а также дирекционного угла этой самой линии. В этом состоит суть. Для получения искомых величин используется вычисление румба и расстояние между координатами точек. Нужно помнить, что дирекционный угол при этом находится по четверти системы координат, которая и является объектом, где размещены искомые позиции. Для решения нужно учитывать знаки приращения, которые свойственны для определенных четвертей. В этом типе задач уделяют большое значение сходимости результатов, поэтому расчеты могут проводиться несколько раз. На это влияют свойства горизонтального положения между точками. В каких случаях применяется обратная геодезическая задача? В тех, когда по известным двум точкам и их координатам определяют расстояние не только между ними, но и дирекционный угол линии.
В том или ином виде геодезические задачи возникают и в других направлениях — в полигонометрии, триангуляции, но на этом не заканчивается востребованность. Используется также, когда стоит задача определения взаимного положения точек по исходным данным длины и направления соединяющей линии. Есть ряд случаев, когда геодезические задачи решают с использованием формул аналитической геометрии в пространстве. Речь идет о пространственных прямоугольных координатах. Для этого используют пространственные компоненты направления прямой линии между этими точками.
Обратный тип геодезической задачи — не просто математическая проверка и вычисления. Она имеет практическое значение, ведь используется при вычислении длин проектных линий. Кроме этого, используется при выполнении привязки теодолитных ходов к пунктам геодезической сети, съемочных сетей и сетей сгущения. Еще одно практическое назначение — определение направления с пункта на пункт при отсутствии видимости. Обратная геодезическая задача используется в промышленном и гражданском строительстве.
А как решать обратные задачи, если в исходнике большие расстояния? В этом случае рекомендуется использовать метод итерации. Его можно использовать при расстояниях до 20 000 км. Итерация основана на решении прямой геодезической задачи любым выбранным методом — численным или аналитическим. И точность решения именно ОГЗ определяется решением ПГЗ.
Прямые и обратные геодезические задачи требуют получения точных результатов. Насколько получится достичь поставленной цели, зависит от исходных сведений и выбранного метода решения. Вычисление способом Бесселя, методом Рунге-Кутта-Фельберга, итерации, численного интегрирования — в каждом отдельном случае выбор зависит от расстояний и координат точек. В штате компании «Промтерра» работают опытные специалисты в сфере инженерной геодезии, поэтому за решение даже самых сложных задач можно быть спокойными. Тема геодезических задач всегда остается актуальной, поэтому отслеживание последних тенденций в проведении вычислений для получения точных результатов — необходимость. Важно отметить, что подобного плана математические методы востребованы не только в геодезической сфере деятельности, но и в навигации, корректировке ракетного огня и др.
Прямая и обратная геодезические задачи на плоскости.
Прямая геодезическая задача. По известным координатам х1 и у1 точки 1, дирекционному углу a1-2 и расстоянию d1-2 до точки 2 требуется вычислить ее координаты х2, у2.
Координаты точки 2 вычисляют по формулам (рис. 3.5):


Обратная геодезическая задача. По известным координатам х1, у1 точки 1 и х2, у2 точки 2 требуется вычислить расстояние между ними d1-2 и дирекционный угол a1-2.
Из формул (3.5) и рис. 3.5 видно, что

Для определения дирекционного угла a1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса
w =
Рис. 3.6. Дирекционные углы и главные значения арктангенса в I, II, III и IV четвертях
Расстояние между точками вычисляют по формуле

или другим путем – по формулам


Программами решения прямых и обратных геодезических задач снабжены, в частности, электронные тахеометры, что дает возможность непосредственно в ходе полевых измерений определять координаты наблюдаемых точек, вычислять углы и расстояния для разбивочных работ.
Оставьте свой комментарий
Оставить комментарий от имени гостя
Комментарии
Закрепленные
Понравившиеся
Последние материалы
Заключение (Грунты)
При построении курса учитывалась необходимость его использования для различных гидротехнических специальностей и специализаций. В качестве основной части для студентов всех гидротехнических специальностей следует считать обязательным прочтение гл. 1—7. В гл. 8.
Представления о решении задач нелинейной механики грунтов
На современном этапе развития нелинейного направления механики грунтов оформились два основных подхода к решению практических задач расчета грунтовых оснований и сооружений: нелинейно-упругий и упругопластический (А. К. Бугров, С. С. Вялов.
Прочность грунтов при сложном напряженном состоянии
Для сред и материалов, обладающих сплошностью, предложено много различных условий прочности. Для оценки прочности грунтов наиболее широкое распространение получило условие Мора—Кулона (2.38), не содержащее промежуточного главного напряжения а2 и тем.
Основные закономерности татического деформирования грунтов
За последние 15. 20 лет в результате многочисленных экспериментальных исследований с применением рассмотренных выше схем испытаний получены обширные данные о поведении грунтов при сложном напряженном состоянии. Поскольку в настоящее время в…
Упругопластическое деформирование среды и поверхности нагружения
Деформации упругопластических материалов, в том числе и грунтов, состоят из упругих (обратимых) и остаточных (пластических). Для составления наиболее общих представлений о поведении грунтов при произвольном нагружении необходимо изучить отдельно закономерности…
Описание схем и результатов испытаний грунтов с использованием инвариантов напряженного и деформированного состояний
При исследовании грунтов, как и конструкционных материалов, в теории пластичности принято различать нагружение и разгрузку. Нагружением называют процесс, при котором происходит нарастание пластических (остаточных) деформаций, а процесс, сопровождающийся изменением (уменьшением)…
Инварианты напряженного и деформированного состояний грунтовой среды
Применение инвариантов напряженного и деформированного состояний в механике грунтов началось с появления и развития исследований грунтов в приборах, позволяющих осуществлять двух- и трехосное деформирование образцов в условиях сложного напряженного состояния…
О коэффициентах устойчивости и сопоставление с результатами опытов
Так как во всех рассмотренных в этой главе задачах грунт считается находящимся в предельном напряженном состоянии, то все результаты расчетов соответствуют случаю, когда коэффициент запаса устойчивости к3 = 1. Для…
Давление грунта на сооружения
Особенно эффективны методы теории предельного равновесия в задачах определения давления грунта на сооружения, в частности подпорные стенки. При этом обычно принимается заданной нагрузка на поверхности грунта, например, нормальное давление р(х), и…
Несущая способность оснований
Наиболее типичной задачей о предельном равновесии грунтовой среды является определение несущей способности основания под действием нормальной или наклонной нагрузок. Например, в случае вертикальных нагрузок на основании задача сводится к тому…
Процесс отрыва сооружений от оснований
Задача оценки условий отрыва и определения требуемого для этого усилия возникает при подъеме судов, расчете держащей силы «мертвых» якорей, снятии с грунта морских гравитационных буровых опор при их перестановке, а…
Решения плоской и пространственной задач консолидации и их приложения
Решений плоской и тем более пространственных задач консолидации в виде простейших зависимостей, таблиц или графиков очень ограниченное число. Имеются решения для случая приложения к поверхности двухфазного грунта сосредоточенной силы (В…
Решение обратной геодезической задачи
Обратная геодезическая задача
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB (рис.24).
Рис. 24. Обратная геодезическая задача
Даннная задача решается следующим образом.
Сначала находим приращения координат:
Величину угла rAB определем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
SAB= ΔX = ΔY = ΔX · sec αAB = ΔY · cosec αAB
SAB= ΔX = ΔY = ΔX · sec rAB = ΔY · cosec rAB
Расстояние SAB можно определить также по формуле
Решение прямой геодезической задачи выполнятеся при помощи следующих формул:
Исходными данными для решения обратной геодезической задачи (определение расстояния между точками и дирекционного угла направления 1-2) являются координаты точек 1 и 2. Инфо
Решение обратной геодезической задачи выполняется при помощи следующи формул:
Правильность вычисления дирекционного угла можно проконтролировать начертив схему с взаимным отображением точек 1 и 2. Если вычисленный по формуле угол не соответсвует схеме, то к полученному значению угла следует прибавить или отнять 180 градусов.
20. (17.1.)
Для определения площади земельных участков существуют различные способы. Применение того или иного способа зависит от наличия планово-картографического материала, значимости и размеров участка, условий местности, цены на землю и требуемой точности.
Способы вычисления площадей:
Геометрические способы используются в тех случаях, когда известны результаты измерения геометрических элементов участка – длины ее линий и величины углов или функций элементов, которыми являются координаты вершин земельного участка.
Механические способы применяются для определения площадей по топографическим планам с помощью механических приборов – планиметров, а также с помощью палеток, представляющих собой прозрачную основу с нанесенной сеткой равных по площади фигур; сторона сетки квадратов обычно составляет 2…10 мм. Палетку кладут на план и внутри контура фигуры подсчитывают число n целых квадратов и число квадратов n1, которые составлены на глаз из частей, рассеченных контуром. Площадь участка определяют по формуле :
Р=р(n-n1), р – площадь одного квадрата в масштабе плана.
Погрешность определения площади палеткой – 0,5…2,0%.
Точность измерения площадей
| Площадь Участка Р, м^3 | Значение погрешности | |||
| 1:500 | 1:1000 | 1:2000 | 1:5000 | 1:10 000 |
| 3,0 | 6,0 | 12,0 | ||
| 3,6 | 7,3 | 14,6 | ||
| 16,4 | 32,8 | 65,6 | ||
| 23,7 | 47,4 | 94,8 | ||
| 10 000 | 47,4 | 94,8 | 186,6 | 948 |
21.(6.2)
Процесс производства геодезических работ включает в себя полевые измерения, составляющие основную часть геодезических работ, и камеральную обработку измереных величин в соответствии с установленными математическими правилами и стандартами.Любую функцию измеренных величин можно назвать косвенно измеренной величиной.Для производства измерений необходимы:объект измерения ;инструменты;исполнитель;определённая естественная среда;метод измерения.С точки зрения условий их выполнения геодезические измерения разделяют на равноточные и неравноточные.
Равноточными измерениями являются однотипные результаты, которые получают при измерениях одним и тем же инструментом, одним и тем же методом.Когда нарушаются эти условия, результаты таких измерений называются неравноточными.
По классу точности результатов измерений их разделяют на высокоточные и технические.Измерения, которые необходимо выполнить, чтобы получить только по одному значению каждой искомой величины, называют необходимыми.Измерения сверх необходимых называют избыточными(не следует путать с понятием лишние!).
Виды измерений.
22. (18.1.)
Погрешность измерения Δ – это отклонение полученного результата от истинного значения измеряемой величины, которое обычно бывает неизвестно, и вопрос о составлении суждений о погрешностях измерений является одним из основных вопросов теории погрешностей измерений. Необходимо знать природу и вид возникновения погрешностей при измерениях. Источников, порождающих это явление, бывает много, и каждый из этих источников порождает часть погрешностей, которые можно назвать элементарными погрешностями.
4 основных вида элементарных погрешностей:
* изменения объекта измерения, происходящие из-за изменений, связанных только с объектами измерений;
* личные погрешности исполнителя;
* погрешности среды (внешние ошибки).
▪ погрешности по абсолютной величине не превосходят некоторого предела, зависящего от точности измерений;
▪ положительные и отрицательные погрешности, равные по абсолютной величине, встречаются в ряду примерно одинаково часто;
▪ чем больше погрешность по абсолютной величине, тем она реже встречается в ряду;
▪ среднее арифметическое значение из случайных погрешностей равноточных измерений при большом числе измерений (n) ничтожно мало, т.е. [Δ]/n
24.(20.1.)
Равноточными измерениями являются однотипные результаты, которые получают при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же(либо аналогичным) методом и в тех же условиях. В тех случаях, когда нарушаются эти условия, результаты таких измерений называются неравноточными.
Арифметическая середина – среднее из измеренных величин:
Х- истинное значение величины, n – количество равноточных измерений.
При неограниченном возрастании числа равноточных измерений одной и той же величины среднее арифметическое стремится к истинному значению этой величины при условии, что измерения содержат неизбежные случайные погрешности
Что такое прямая и обратная геодезическая задача?
Основной профиль компании БРИГС – геодезические работы в строительстве. Мы стараемся предоставлять информацию о нашей деятельности в как можно более доступной форме. Довольно часто нас спрашивают о геодезической задаче – что это, какими методами она решается и какие результаты приносит ее выполнение? На эти вопросы мы постараемся ответить в данном обзоре.
Что такое геодезическая задача?
Итак, геодезическая задача заключается в определении взаимного положения заданных точек на поверхности земли. В том или ином виде она возникает при обработке триангуляции и полигонометрии, то есть в процессе создания сети опорных пунктов геодезии. Геодезическая задача бывает прямой и обратной.
Прямая геодезическая задача решается методом вычисления широты и долготы конкретной точки, которая лежит на условном земном эллипсоиде. При этом необходимо знать координаты другой точки, а также длину и дирекционный угол направления, соединяющего обе эти позиции. Обратная геодезическая задача заключается в определении длины и дирекционного угла направления между точками на земном эллипсоиде с исходными геодезическими координатами.
Прямая геодезическая задача.
Решение задач данного типа проводится с помощью формул нахождения приращений и определения координат. Возможность и точность расчета координат точек зависит от корректности исходных данных, а также применяемой методики. Решение прямой геодезической задачи может осуществляться косвенными или прямыми методами.
Что касается первых, они являются весьма чувствительными к исходным данным и не работают при наличии значительных расстояний и изменений азимута, в частности, в северных широтах. Прямые же методы позволяют получить достаточно точные координаты по соотношениям сфероидической геодезии.
Обратная геодезическая задача.
В данном случае искомые величины рассчитываются с помощью вычисления румба и расстояния между заданными точками. При этом угол дирекции находится по четверти системы координат, в которой размещены искомые позиции.
Решение обратной геодезической задачи проводится с учетом знаков приращений. В свою очередь последние свойственны той или иной четверти. Правильность решения определяется сходимостью результатов вычислений, которые проводятся несколько раз в зависимости от свойств горизонтального проложения между расчетными точками.
Прямая и обратная геодезические задачи. Их применение в геодезическом производстве



а) Прямая геодезическая задача
Рис. 3.5. Прямая геодезическая задача
Дано: координаты точки 1 х1, у1; горизонтальное проложение линии 1 – 2: d1,2;
дирекционный угол линии 1 – 2: a1,2 (рис.3.5).
Найти: координаты точки 2: х2, у2.
Решение: координаты точки 2: х2 = х1 + Dх; у2 = у1 + Dу, (3.6)
где приращения координат Dх = d · cos a; Dу = d · sin a, (3.7)
Знаки приращений координат Dх и Dу зависят от знаков функций sin a и cos a.
б) Обратная геодезическая задача
 |
Рис. 3.6. Обратная геодезическая задача
Найти: горизонтальное проложение линии 1 – 2: d1,2; дирекционный угол линии 1 – 2: a1,2.
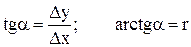
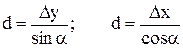
По значению tg a определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
Рис. 3.7. Знаки приращений координат в зависимости от четверти
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.







