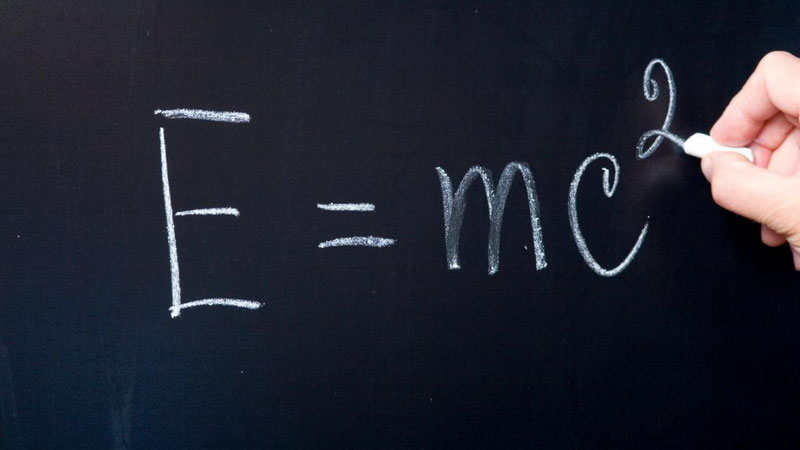Что значит релятивистский в физике

Релятивистская физика

Специальная теория относительности

Специальная, или частная теория относительности — это теория структуры пространства-времени. Впервые была представлена в 1905 году Альбертом Эйнштейном в работе «К электродинамике движущихся тел». Теория описывает движение, законы механики, а также пространственно-временные отношения, определяющие их, при скоростях движения, близких к скорости света. Классическая механика Ньютона в рамках специальной теории относительности является приближением для малых скоростей.

Общая теория относительности

Общая теория относительности — теория гравитации, разработанная Эйнштейном в 1905—1917 годах. Является дальнейшим развитием специальной теории относительности. В общей теории относительности постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, а деформацией самого пространства-времени, в котором они находятся. Эта деформация связана, в частности, с присутствием массы-энергии.

Ссылки

Полезное

Смотреть что такое «Релятивистская физика» в других словарях:

Физика и реальность — «ФИЗИКА И РЕАЛЬНОСТЬ» сборник статей А. Эйнштейна, написанных в разные периоды его творческой жизни. Рус. издание М., 1965. В книге нашли отражение основные эпистемологические и методологические воззрения великого физика. Среди них… … Энциклопедия эпистемологии и философии науки

Релятивистская теория гравитации — (РТГ) теория гравитации, основанная на представлении гравитационного поля как симметричного тензорного физического поля валентности 2 в пространстве Минковского. Разрабатывается академиком РАН А. А. Логуновым с группой… … Википедия

ФИЗИКА — (греч. τὰ φυσικά – наука о природе, от φύσις – природа) – комплекс науч. дисциплин, изучающих общие свойства структуры, взаимодействия и движения материи. В соответствии с этими задачами совр. Ф. весьма условно можно подразделить на три больших… … Философская энциклопедия

Физика гиперядер — Физика гиперядер раздел физики на стыке ядерной физики и физики элементарных частиц, в котором предметом исследования выступают ядроподобные системы, содержащие кроме протонов и нейтронов другие элементарные частицы гипероны. Также… … Википедия

Физика ускорителей — раздел физики, изучающий динамику частиц в ускорителях, а также многочисленные технические задачи, связанные с сооружением и эксплуатацией ускорителей частиц. Физика ускорителей включает в себя вопросы, связанные с получением и накоплением частиц … Википедия

ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия

Релятивистская механика — Релятивистская механика раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую)… … Википедия

Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия

Физика — Примеры разнообразных физических явлений Физика (от др. греч. φύσις … Википедия

Источник

Релятивистская физика

Содержание

Отличия СТО от ньютоновской механики

Впервые новая теория потеснила 200-летнюю механику Ньютона. Это в корне изменило восприятие мира. Классическая механика Ньютона оказалась верной лишь в земных и близких к ним условиях: при скоростях намного меньше скорости света и размерах, значительно превышающих размеры атомов и молекул и при расстояниях или условиях, когда скорость распространения гравитации можно считать бесконечной.

Ньютоновские понятия о движении были кардинально скорректированы посредством нового достаточно глубокого применения принципа относительности движения. Время уже не было абсолютным (а начиная с ОТО — и равномерным).

Более того, Эйнштейн изменил фундаментальные взгляды на время и пространство. Согласно теории относительности, время необходимо воспринимать как почти равноправную составляющую (координату) пространства-времени, которая может участвовать в преобразованиях координат при изменении системы отсчёта вместе с обычными пространственными координатами, подобно тому, как преобразуются все три пространственные координаты при повороте осей обычной трёхмерной системы координат.

Область применимости

Область применимости СТО

Специальная теория относительности применима для изучения движения тел с любыми скоростями (в том числе близкими или равными скорости света) при условии отсутствия очень сильных гравитационных полей.

Область применимости ОТО

Общая теория относительности применима для изучения движения тел с любыми скоростями в гравитационных полях любой интенсивности, если квантовыми эффектами можно пренебречь.

Применение

Применение СТО

Специальная теория относительности применяется в физике и астрономии начиная с XX века. Теория относительности значительно расширила понимание физики в целом, а также существенно углубила знания в области физики элементарных частиц, дав мощнейший импульс и серьёзные новые теоретические инструменты для развития физики, значение которых трудно переоценить.

Применение ОТО

С помощью данной теории космология и астрофизика сумели предсказать такие необычные явления, как нейтронные звезды, чёрные дыры и гравитационные волны.

Принятие научным сообществом

Принятие СТО

Принятие ОТО

Особенно продуктивно было конструктивное обсуждение принципиальных вопросов общей теории относительности (Шрёдингер и др.), фактически это обсуждение продолжается до сих пор.

Специальная теория относительности

Специальная теория относительности [7] (СТО) — теория локальной структуры пространства-времени. Впервые была представлена в 1905 году Альбертом Эйнштейном в работе «К электродинамике движущихся тел». Теория описывает движение, законы механики, а также пространственно-временные отношения, определяющие их, при любых скоростях движения, в том числе и близких к скорости света. Классическая механика Ньютона в рамках специальной теории относительности является приближением для малых скоростей. СТО может применяться там, где можно ввести инерциальные системы отсчёта (хотя бы локально); она неприменима для случаев сильных гравитационных полей, существенно неинерциальных систем отсчёта и при описании глобальной геометрии Вселенной (кроме частного случая плоской пустой стационарной Вселенной).

Специальная теория относительности возникла как разрешение противоречия между классической электродинамикой (включая оптику) и классическим галилеевским принципом относительности. Последний утверждает, что все процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения. Это означает, в частности, что любые механические эксперименты в закрытой системе не позволят определить без наблюдения внешних по отношению к ней тел, как она движется, если её движение равномерно и прямолинейно. Однако оптические эксперименты (например, измерение скорости распространения света в разных направлениях) внутри системы в принципе должны были бы обнаружить такое движение. Эйнштейн распространил принцип относительности и на электродинамические явления, что, во-первых, дало возможность описать практически весь круг физических явлений с единых позиций, а во-вторых, позволило объяснить результаты эксперимента Майкельсона — Морли (в котором не было обнаружено никакого влияния квазиинерциального движения Земли на скорость распространения света). Принцип относительности стал первым постулатом новой теории. Однако непротиворечивое описание физических явлений в рамках расширенного принципа относительности стало возможным лишь ценой отказа от ньютоновского абсолютного евклидового пространства и абсолютного времени и их объединения в новый геометрический конструкт — псевдоевклидово пространство-время, в котором расстояния и временные промежутки между событиями трансформируются определённым образом (посредством преобразований Лоренца) в зависимости от системы отсчёта, из которой они наблюдаются. Это потребовало введения дополнительного принципа — постулата инвариантности скорости света. Таким образом, специальная теория относительности базируется на двух постулатах:

1. Все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

2. Скорость света в вакууме, измеренная в любой инерциальной системе отсчёта, одна и та же и не зависит от движения излучателя.

Следствием второго принципа (и общенаучного принципа причинности) является невозможность движения физических тел и передачи информации со скоростью, превышающей скорость света в вакууме.

При движении со скоростями, малыми по сравнению со скоростью света, кинематика СТО неотличима от ньютоновской кинематики, а преобразования Лоренца переходят в классические преобразования Галилея. Формально в пределе бесконечной скорости света формулы специальной теории относительности переходят в формулы классической механики.

Общая теория относительности

Общая теория относительности — теория гравитации, опубликованная Эйнштейном в 1915—1916 годах. Является дальнейшим развитием специальной теории относительности. В общей теории относительности постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, а деформацией самого пространства-времени, в котором они находятся. Эта деформация связана, в частности, с присутствием массы-энергии.

Общая теория относительности отличается от других метрических теорий тяготения использованием уравнений Эйнштейна для связи кривизны пространства-времени с присутствующей в нём материей.

ОТО в настоящее время — самая успешная теория гравитации, хорошо подтверждённая наблюдениями.

Источник

Понятие релятивистской механики

Обновлено: 05 Июля 2021

Мы понимаем принципы работы классической механики. Однако какие законы действуют на скоростях, близких к скорости света? В этой статье расскажем об основных законах релятивистской механики.

Что такое релятивистская механика

Релятивистская механика изучает движение частиц, у которых скорость близка к скорости света. Этот раздел появился на стыке механики, специальной теории относительности и общей теории относительности.

В основе лежат два постулата:

Основной закон релятивистской механики

Сформулировать основную теорию релятивистской механики можно следующим образом: скорость изменения импульса физического тела равняется силе, действующей на точку. Такая формулировка этой теории формально совпадает со вторым законом Ньютона.

Первое положение универсальной теории относительности говорит о том, что формы фундаментальных постулатов физики во всех существующих инерциальных системах отсчета должны обязательно сохраняться.

В то же время основной закон динамики Ньютона выражается уравнением, в котором масса m является абсолютной и одинаковой во всех инерциальных системах отсчета. И при переходе от одной системы отсчета к другой форма записи закона также будет кардинально видоизменяться. Из чего можно сделать вывод о том, что этот закон не может стать базой для релятивистской динамики.

Эйнштейном было доказано, что форма второго закона Ньютона сохранится, если под общей массой понимать коэффициент, измеряющийся только в инерциальной системе отсчета при помощи материальной точки и скорости света в пустоте.

Закон взаимосвязи массы и энергии

Закон соотношения между массой и энергией можно выразить следующей формулой:

Тело обладает энергией и при нулевой скорости. Такая энергия называется энергией покоя.

Полную энергию свободного тела можно приравнять к произведению его релятивистской массы на квадрат скорости света в вакууме: \(E = mc^2\)

При этом нельзя говорить, что масса переходит в энергию. Осуществляется переход из одной формы энергии в другую. Однако любое превращение энергии сопровождается превращением массы.

Преобразование Лоренца

Преобразования, в основе которых лежат постулаты Эйнштейна, называются преобразованиями Лоренца.

В свою очередь в преобразованиях Лоренца он равен \(y.\)

Расчет для \(t\) в преобразованиях Лоренца будет иметь следующий вид:

Следствия из преобразований Лоренца:

где \(Δt \) – промежуток времени между событиями, а \(Δt0\) – собственное время.

где \(l0\) – собственная длина.

Проекция скорости материальной точки на координатные оси в системе \(K\) :

Проекция скорости материальной точки на координатные оси в системе \(K\) ’:

Принцип относительности в релятивистской механике

Принцип относительности – базовый постулат теории Эйнштейна, в котором говорится о том, что все физические процессы проходят единовременно и одинаково во всех инерциальных системах отсчета. Но в релятивистской механике теория относительности основывается не только на первом постулате, но и на втором, суть которого заключается в том, что скорость света в пустоте равна для всех существующих в той же среде инерциальных систем отсчета. На нее не влияют ни скорость светового сигнала, ни скорость самого источника.

Следствия, которые вытекают из постулатов теории относительности:

Если вам нужна курсовая, дипломная работа по этой или другой теме, авторы ФениксХелп отлично справятся с такой задачей.

Источник

Основы механики для «чайников» (часть 3): релятивистская механика

Релятивистская механика – это механика, в которую превращается механика Ньютона в случае если тело движется со скоростью, близкой к скорости света. На таких высоких скоростях с вещами начинают происходить ну просто волшебные и совершенно неожиданные вещи, такие как, например, релятивистское сокращение длины или замедление времени.

Но как именно классическая механика становится релятивистской? Обо всем по порядку в нашей новой статье.

Начнем с самого начала.

Принцип относительности Галилея

Принцип относительности Галилея (1564-1642) гласит:

В инерциальных системах отсчета все процессы протекают одинаково, если система неподвижна или движется равномерно и прямолинейно.

В данном случае речь идет исключительно о механических процессах. Что это значит? Это значит, что если мы, например, будем плыть на равномерно и прямолинейно движущемся пароме через туман, мы не сможем определить, движется паром или покоится. Иными словами, если провести эксперимент в двух одинаковых замкнутых лабораториях, одна из которых равномерно и прямолинейно движется относительно другой, результат эксперимента будет одинаковым.

Преобразования Галилея

Преобразования Галилея в классической механике – это преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Не будем приводить здесь всех вычислений и выводов, а просто запишем формулу для преобразования скорости. Согласно этой формуле скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела в движущейся системе отсчета и скорости движущейся системы отсчета относительно неподвижной.

Приведенный нами выше принцип относительности Галилея является частным случаем принципа относительности Эйнштейна.

Принцип относительности Эйнштейна и постулаты СТО

В начале двадцатого века после более чем двухсотлетнего господства классической механики возник вопрос о распространении принципа относительности на немеханические явления. Причиной возникновения такого вопроса стало закономерное развитие физики, в частности оптики и электродинамики. Результаты многочисленных экспериментов то подтверждали справедливость формулировки принципа относительности Галилея для всех физических явлений, то в ряде случаев указывали на ошибочность преобразований Галилея.

Например, проверка формулы сложения скоростей показала ее ошибочность при скоростях, близких к скорости света. Более того, опыт Физо в 1881 году показал, что скорость света не зависит от скорости движения источника и наблюдателя, т.е. в любой системе отсчета остается постоянной. Данный результат эксперимента никак не укладывался в рамки классической механики.

Первый постулат: во всех инерциальных системах отсчета все физические явления протекают одинаково. При переходе от одной системы к другой все законы природы и явления, описывающие их, инвариантны, то есть никакими опытами нельзя отдать предпочтение одной из систем, ибо они инвариантны.

Второй постулат: скорость света в вакууме одинакова во всех направлениях и не зависит от источника и наблюдателя, т.е. не изменяется при переходе от одной инерциальной системы к другой.

Скорость света – предельная скорость. Никакой сигнал или действие не могут распространяться со скоростью, превышающей скорость света.

Преобразования координат и времени при переходе от неподвижной системы отсчета к системе, движущейся со скоростью света, называются преобразованиями Лоренца. К примеру, пусть одна система покоится, а вторая движется вдоль оси абсцисс.

Как видим, время также изменяется наряду с координатами, то есть выступает как бы в роли четвертной координаты. Преобразования Лоренца показывают, что в СТО пространство и время неразделимы в отличие от классической механики.

Помните парадокс двух близнецов, один из которых ждал на земле, а второй летел на космическом корабле с очень большой скоростью? После того как брат-космонавт вернулся на землю, он застал своего брата стариком, хотя сам был практически так же молод, как в момент начала путешествия. Типичный пример того, как изменяется время в зависимости от системы отсчета.

При скоростях же много меньших скорости света преобразования Лоренца переходят в преобразования Галилея. Даже при скорости современных реактивных самолетов и ракет отклонения от законов классической механики настолько малы, что их практически невозможно измерить.

Релятивистская механика

Механика, учитывающая преобразования Лоренца, и называется релятивистской.

В рамках релятивистской механики меняются формулировки некоторых физических величин. Например, импульс тела в релятивистской механике в соответствии с преобразованиями Лоренца может быть записан так:

Соответственно, второй закон Ньютона в релятивистской механике будет иметь вид:

А полная релятивистская энергия тела в релятивистской механике равна

Если тело покоится и скорость равна нулю, данная формула преобразуется в знаменитую

Формула энергии покоя тела

Данная формула, которую, кажется, знают все, показывает, что масса является мерой полной энергии тела, а также иллюстрирует принципиальную возможность перехода энергии вещества в энергию излучения.

Дорогие друзья, на этой торжественной ноте мы закончим наш сегодняшний обзор релятивистской механики. Мы рассмотрели принцип относительности Галилея и Эйнштейна, а также некоторые основные формулы релятивистской механики. Самым стойким и дочитавшим статью до конца напоминаем – в мире нет «нерешабельных» задач и проблем, которые невозможно решить. Паниковать и переживать из-за незаконченной курсовой нет никакого смысла. Просто вспомните о масштабах Вселенной, вздохните полной грудью и поручите выполнение настоящим профессионалам своего дела – авторам компании Zaochnik.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Уравнения усложняются в более привычных трехмерный векторное исчисление формализм, благодаря нелинейность в Фактор Лоренца, который точно учитывает релятивистскую зависимость скорости и Ограничение скорости всех частиц и полей. Однако они имеют более простую и элегантную форму в четыре-размерный пространство-время, который включает квартиру Пространство Минковского (SR) и искривленное пространство-время (GR), потому что трехмерные векторы, полученные из пространства, и скаляры, полученные из времени, могут быть собраны в четыре вектора, или четырехмерный тензоры. Однако шестикомпонентный тензор углового момента иногда называют бивектором, потому что с трехмерной точки зрения это два вектора (один из них, обычный угловой момент, является осевой вектор).

Содержание

Релятивистская кинематика

Релятивистская четырехскорость, то есть четырехвектор, представляющий скорость в теории относительности, определяется следующим образом:

В приведенном выше описании τ < displaystyle < tau>> это подходящее время пути через пространство-время, называемая мировой линией, за которой следует скорость объекта, представленная выше, и

(можно цитировать любую версию), поэтому следует:

Релятивистская динамика

Масса покоя и релятивистская масса

Лев Окун предположил, что концепция релятивистской массы «сегодня не имеет рационального оправдания» и ее больше не следует преподавать. [3] Другие физики, в том числе Вольфганг Риндлер и Т. Р. Сандин, утверждают, что концепция полезна. [4] Увидеть масса в специальной теории относительности для получения дополнительной информации об этой дискуссии.

Частица, масса покоя которой равна нулю, называется безмассовый. Фотоны и гравитоны считаются безмассовыми, и нейтрино почти так.

Релятивистская энергия и импульс

Есть несколько (эквивалентных) способов определения импульса и энергии в СТО. Один метод использует законы сохранения. Если эти законы должны оставаться в силе в СТО, они должны выполняться во всех возможных системах отсчета. Однако, если сделать несколько простых мысленные эксперименты используя ньютоновские определения импульса и энергии, можно увидеть, что эти величины не сохраняются в СТО. Можно спасти идею сохранения, внеся небольшие изменения в определения, чтобы учесть релятивистские скорости. Именно эти новые определения принимаются за правильные для импульса и энергии в СИ.

В четырехимпульсный объекта проста, идентична по форме классическому импульсу, но заменяет 3-векторы на 4-векторы:

Энергия и импульс объекта с инвариантной массой м 0 < displaystyle m_ <0>> , двигаясь с скорость v < displaystyle mathbf > относительно данной системы отсчета, соответственно задаются

а скорость как функция кинетической энергии определяется выражением

Простое соотношение между энергией, импульсом и скоростью может быть получено из определений энергии и импульса путем умножения энергии на v < displaystyle mathbf > , умножая импульс на c 2 < displaystyle c ^ <2>> , и отметив, что эти два выражения равны. Это дает

Инвариантная масса системы может быть записана как

м 0 малыш = E малыш 2 − ( п малыш c ) 2 c 2 < displaystyle > _ < text > = < frac < sqrt > ^ <2>— (p _ < text > c) ^ <2>>> >>>

Из-за кинетической энергии и энергии связи эта величина отличается от суммы масс покоя частиц, из которых состоит система. Масса покоя не является постоянной величиной в специальной теории относительности, в отличие от ситуации в ньютоновской физике. Однако даже если объект изменяется внутри, пока он не обменивается энергией или импульсом со своим окружением, его масса покоя не изменится и может быть вычислена с тем же результатом в любой системе отсчета.

Эквивалентность массы и энергии

Релятивистское уравнение энергии-импульса справедливо для всех частиц, даже для безмассовые частицы для которого м₀ = 0. В этом случае:

При замене на Ev = c 2 п, это дает v = c: безмассовые частицы (например, фотоны) всегда движутся со скоростью света.

Обратите внимание, что масса покоя составной системы, как правило, будет немного отличаться от суммы масс покоя ее частей, поскольку в системе покоя их кинетическая энергия увеличит ее массу, а их (отрицательная) энергия связи уменьшит ее массу. В частности, гипотетический «ящик света» имел бы массу покоя, даже если бы он был сделан из частиц, которые не имеют, поскольку их импульсы сокращаются.

Глядя на приведенную выше формулу для инвариантной массы системы, можно увидеть, что когда один массивный объект находится в состоянии покоя (v = 0, п = 0) осталась ненулевая масса: м₀ = E/c 2 Соответствующая энергия, которая также является полной энергией, когда отдельная частица находится в состоянии покоя, называется «энергией покоя». В системах частиц, которые наблюдаются из движущейся инерциальной системы отсчета, полная энергия увеличивается, как и импульс. Однако для отдельных частиц масса покоя остается постоянной, а для систем частиц инвариантная масса остается постоянной, потому что в обоих случаях энергия и импульс увеличиваются, вычитаются друг из друга и сокращаются. Таким образом, инвариантная масса систем частиц является вычисляемой константой для всех наблюдателей, как и масса покоя отдельных частиц.

Масса систем и сохранение инвариантной массы

Для систем частиц уравнение энергии-импульса требует суммирования векторов импульса частиц:

Инерциальная система отсчета, в которой импульсы всех частиц равны нулю, называется центр импульса кадра. В этой специальной системе отсчета релятивистское уравнение энергии-импульса имеет п = 0 и, таким образом, дает инвариантную массу системы как просто полную энергию всех частей системы, деленную на c 2

Это инвариантная масса любой системы, которая измеряется в системе отсчета, где она имеет нулевой общий импульс, например, баллон с горячим газом на весах. В такой системе масса, которую взвешивают весы, является инвариантной массой, и она зависит от полной энергии системы. Таким образом, это больше, чем сумма масс покоя молекул, но также включает в себя все суммарные энергии в системе. Подобно энергии и импульсу, инвариантная масса изолированных систем не может быть изменена до тех пор, пока система остается полностью закрытой (масса или энергия не допускаются внутрь или наружу), потому что полная релятивистская энергия системы остается постоянной, пока ничто не может войти или выйти. Оставь это.

Увеличение энергии такой системы, вызванное переводом системы в инерциальную систему отсчета, которая не является центр импульса кадра, вызывает увеличение энергии и количества движения без увеличения инвариантной массы. E = м₀c 2 однако применимо только к изолированным системам в их системе отсчета центра импульса, где сумма импульса равна нулю.

Закрытые (изолированные) системы

В «полностью закрытой» системе (т. Е. изолированная система) полная энергия, полный импульс и, следовательно, полная инвариантная масса сохраняются. Формула Эйнштейна для изменения массы переводится в простейшую формулу ΔE = ΔMC 2 форма, однако, только в незамкнутых системах, в которых энергия может уйти (например, в виде тепла и света), и, таким образом, инвариантная масса уменьшается. Уравнение Эйнштейна показывает, что такие системы должны терять массу в соответствии с приведенной выше формулой пропорционально энергии, которую они теряют в окружающую среду. И наоборот, если можно измерить разницу в массе между системой до того, как она подвергнется реакции, которая высвобождает тепло и свет, и системой после реакции, когда тепло и свет ушли, можно оценить количество энергии, которая ускользает из системы.

Химические и ядерные реакции

Центр импульса кадра

Уравнение E = м₀c 2 применяется только к изолированным системам в их центр импульса кадра. Обычно это неправильно понимается как означающее, что масса может быть преобразованный к энергии, после чего масса исчезает. Однако популярные объяснения уравнения применительно к системам включают открытые (неизолированные) системы, в которых теплу и свету позволено улетучиваться, хотя в противном случае они внесли бы свой вклад в массу (инвариантная масса) системы.

Исторически сложилось так, что путанице с «преобразованием» массы в энергию способствовала путаница между массой и «дело», где материя определяется как фермион частицы. В таком определении электромагнитное излучение и кинетическая энергия (или тепло) не считаются «материей». В некоторых ситуациях материя действительно может быть преобразована в нематериальные формы энергии (см. Выше), но во всех этих ситуациях материальные и нематериальные формы энергии все еще сохраняют свою первоначальную массу.

Угловой момент

В релятивистской механике изменяющийся во времени момент массы

и орбитальный 3-угловой момент

точечной частицы объединяются в четырехмерный бивектор в плане 4-х позиционного Икс и 4-импульс п частицы: [8] [9]

Каждый из шести компонентов образует сохраняемую величину при агрегировании с соответствующими компонентами для других объектов и полей.

В специальной теории относительности Второй закон Ньютона не держится в форме F = ма, но это так, если это выражается как

Проведение производных дает

По конструкции а_∥ и v параллельны, поэтому (v·а_∥)v вектор с величиной v 2 а_∥ в направлении v (и, следовательно а_∥) что позволяет заменить:

Следовательно, в некоторых старых текстах γ (v) 3 м₀ называется продольная масса, а γ (v)м₀ называется поперечная масса, который численно совпадает с релятивистская масса. Увидеть масса в специальной теории относительности.

Если инвертировать это, чтобы вычислить ускорение от силы, получится

Сила, описанная в этом разделе, является классической трехмерной силой, которая не является четырехвекторный. Эта трехмерная сила является подходящим понятием силы, поскольку это сила, которая подчиняется Третий закон движения Ньютона. Не следует путать с так называемым четыре силы которая представляет собой всего лишь трехмерную силу в сопутствующей рамке объекта, преобразованного, как если бы он был четырехвекторным. Однако плотность 3-D силы (количество движения, передаваемое на единицу четырехтомный) является четырехвектор (плотность веса +1) в сочетании с отрицательным значением плотности передаваемой мощности.

Крутящий момент

Крутящий момент, действующий на точечную частицу, определяется как производная тензора углового момента, указанного выше, по собственному времени: [10] [11]

Γ = d M d τ = Икс ∧ F < displaystyle < boldsymbol < Gamma>> = < frac > > = mathbf wedge mathbf >

или в компонентах тензора:

Кинетическая энергия

В теорема об энергии работы говорит [12] изменение в кинетическая энергия равно работе, проделанной над телом. В специальной теории относительности:

Если в исходном состоянии тело было в покое, значит v₀ = 0 и γ₀(v₀) = 1, а в конечном состоянии имеет скорость v₁ = v, полагая γ₁(v₁) = γ (v) кинетическая энергия равна;

Ньютоновский предел

Для скоростей, намного меньших скорости света, можно пренебречь членами с c 2 и выше в знаменателе. Эти формулы затем сводятся к стандартным определениям ньютоновского кинетическая энергия и импульс. Так и должно быть, поскольку специальная теория относительности должна согласовываться с ньютоновской механикой при малых скоростях.

Источник