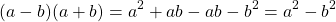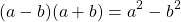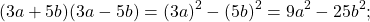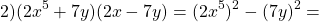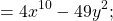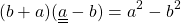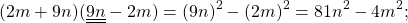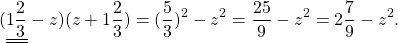Что значит произведение суммы и разности чисел
Произведение суммы и разности
Произведение суммы и разности двух выражений можно найти как произведение многочленов. Для ускорения вычислений удобнее вывести формулу.
Найдем произведение суммы и разности двучленов непосредственным умножением:
-ab и +ab — противоположные слагаемые, поэтому их сумма равна нулю.
Произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Формула произведения суммы и разности:
Произведение суммы и разности двух выражений можно изобразить схематически так:
Рассмотрим на примерах, как находить произведение суммы и разности двух выражений с помощью схемы и с помощью формулы.
Если все, что стоит до «+» и до «-«, заключить в квадрат, все, что после этих знаков — в круг, то произведение суммы (3a+5b) и разности (3a-5b) с помощью схемы можно представить так:
Чтобы применить форму произведения суммы разности, найдем a и b. В данном примере a=3a, b=3b:
Важно помнить — при возведении в квадрат произведения нескольких множителей, дроби или степени их обязательно следует записывать в скобках!
Как найти произведение суммы и разности, если слагаемые в скобках поменять местами?
От перестановки мест слагаемых сумма не меняется. Поэтому в разности квадратов на первое месте нужно поставить то выражение, которое стоит на первом месте в разности. Например,
Произведение разности и суммы двух выражений
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Муниципальное образовательное учреждение Воскресенская средняя школа Воскресенского района Нижегородской области
Произведение суммы и разности двух выражений
Произведение разности и суммы двух выражений (первый урок по данной теме)
Урок открытия нового
Ознакомление с правилом произведения разности и суммы двух выражений, формирование умения применять изученное правило при выполнении упражнений
— «открыть» правило и формулу произведения разности и суммы двух выражений;
-научиться применять правило произведения разности и суммы двух выражений;
-развивать аналитические операции (сравнение, анализ, синтез, обобщение);
-развивать исследовательские умения
-воспитывать коммуникативные компетенции;
-формировать умение самостоятельно определять цели своего обучения;
-воспитывать настойчивость и целеустремленность;
-воспитывать интерес к предмету.
Формы организации учебной деятельности
Фронтальная, индивидуальная, парная
Структура и ход урока
Мотивационно- ориентировочная часть
Организовать мотивацию обучающихся к учебной деятельности на уроке
Сегодня предлагаю начать урок с прочтения притчи.
Как вы думаете, почему учитель так ответил своему ученику? Много ли еще загадок вокруг нас, а в математике?
Я желаю, чтобы сегодня на уроке вы открыли еще одну тайну. И тогда тайн у вас останется на одну меньше.
1)Организовать актуализацию изученных способов действий, достаточных для построения нового знания
2) Организовать самостоятельное выполнение пробного учебного действия
3)Организовать фиксацию индивидуальных затруднений в выполнение пробного учебного действия
-Прочитайте выражения, записанные на доске, сравните их, что вы заметили?
-Хорошо, выполните умножение известным способом, а можно ли прийти к результату более легким и быстрым способом, чем тот который мы использовали?
-Свойство возведения произведения в степень и возведение степени в степень (проговаривают формулировки и записывают формулы)
(х 2 – у 3 ) (х 2 + у 3 )
— Это аналогичные выражения, мы их можем упростить, применив правило умножения многочленов
(Сравнивая результаты, замечают, что можно получить ответ, минуя промежуточные преобразования)
III этап: постановка учебной задачи и планирование ее решения — 1 мин.
Организовать построение проекта выхода из затруднения: учащиеся согласовывают тему урока, учебную задачу, формулируют шаги, которые необходимо сделать для реализации поставленной задачи
-Сформулируйте цель дальнейшей деятельности
-Уточните, какое правило мы должны «открыть»
-Сформулируйте тему урока
Узнать новое правило, научиться его применять
Произведение разности и суммы двух выражений.
Организовать реализацию построенного проекта
-Сравните полученные результаты, попытайтесь сделать вывод.
-А как записать в общем виде?
-Составьте его схему.
-Что нужно сделать, чтобы получилась формула?
-Попробуйте дать словесную формулировку
-Как проверить правильные ли у нас получились выводы? стр.92 учебника.
— Для чего оно нужно, ведь мы и раньше умели выполнять умножение?
-Поэтому это тождество называют формулой сокращенного умножения.
-Замечают, что можно получить ответ, минуя промежуточные преобразования
-Сверить с учебником
-Делают выводы: при умножении разности выражений на их сумму можно сократить работу, сразу записав результат-разность квадратов этих выражений. Значит этой формулой пользоваться рационально.
Организовать усвоение детьми нового способа действий при решении задач с проговариванием во внешней речи
Что сейчас вы должны сделать?
1.Выполните умножение, сопоставляя каждое свое действие с полученным правилом
5) 
2. №502(нечетные) для ребят 1 варианта, №502(четные) – для 2 варианта. Затем поменяйтесь тетрадями и проверьте решение у своего соседа. Сверьте свои решения и решения пары, работающей у доски.(Приложение2)
Потренироваться в применении
(фронтальная форма работы)
VI этап: самостоятельная работа с самопроверкой по эталону-5 мин
Организовать самостоятельное выполнение обучающимся типовых заданий на новый способ действий;
организовать соотнесение работы с эталоном для самопроверки
Если вы выполнили все задания правильно и не испытываете затруднений, то №517(повышенного уровня сложности), если еще остались затруднения, то потренируйтесь еще
Самостоятельное решение задач и самопроверка по образцу или решение заданий с помощью учителя и демонстрация решения на доске
VIII этап: Включение в систему знаний-5 мин
Организовать выполнение задания, где используется новый способ действий
Недавно на страницах журнала я прочла статью о том, что семиклассники одной из школ могут устно решить такие примеры
А вы сможете устно посчитать?
Какое знание нам в этом поможет?
Рефлексивно – оценочный компонент
Организовать рефлексивный анализ учебной деятельности
_Что нового вы сегодня узнали?
– Какую цель ставили перед собой?
– Достигнута ли поставленная цель?
– Как вы ее достигали?
− Где вы сможете применить новые знания?
Дети соотносят учебную задачу и её результаты.
Отвечают на поставленные вопросы
Х этап: оценка собственной деятельности-1 мин
Организовать оценивание учащимися собственной деятельности
Что нужно сделать тем ученикам, у которых еще остались затруднения? А тем ученикам, у кого не осталось вопросов и затруднений надо тренироваться или нет? Где вы еще можете потренироваться по теме нашего урока?
дома, на следующем уроке
ХI этап: информация о домашнем задании – 2 мин.
Организовать обсуждение и записать домашнего задания
п. 14 №503, 518, самостоятельно составить 2 задания, аналогичные тем, что решали в классе.
— Как вы думаете, давно ли известны людям формулы сокращенного умножения? Подготовьте историческую справку
СПАСИБО всем за активную работу на уроке!
Воспринимают информацию, записывают в дневники домашнее задание
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Разность суммы это как?
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.
Деление есть операция, обратная умножению.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Как найти разность чисел в математике
Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
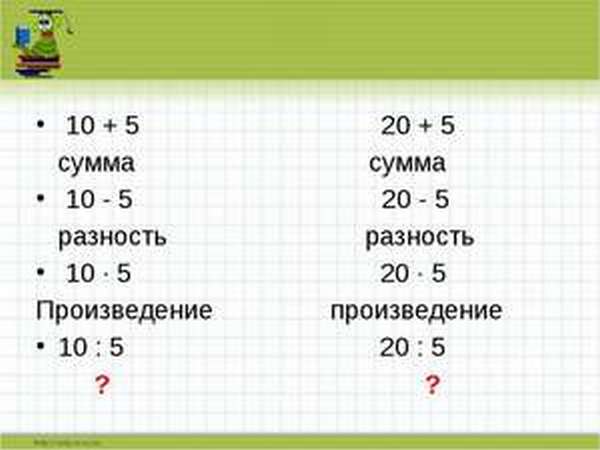
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
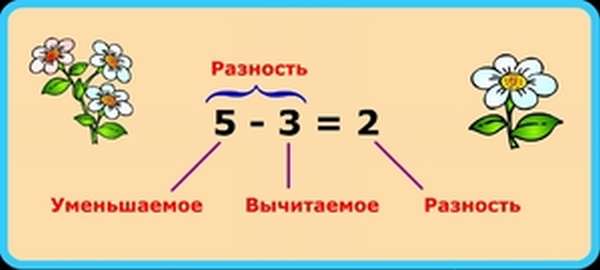
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Простые примеры
20 — уменьшаемое значение,
Ответ: 5 — разница величин.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
17 — уменьшаемая величина.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
Даны целые значения: 56, 12, 4.
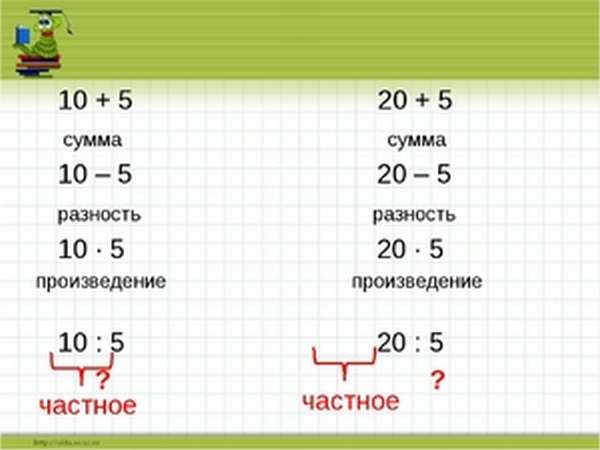
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
7 — уменьшаемая величина,
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий: