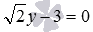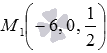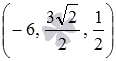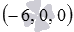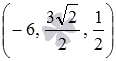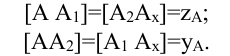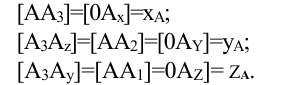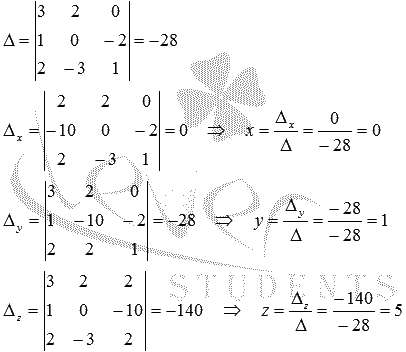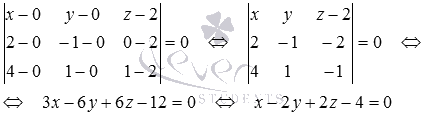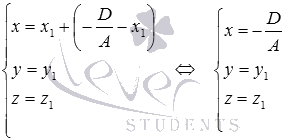Что значит проекция точки
Проекция точки на плоскость, координаты проекции точки на плоскость
В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
— получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
Рассмотрим теорию на практических примерах.
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Составим систему уравнений:
И решим ее, используя метод Крамера:
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Теперь, имея координаты точки прямой М 1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
Затем определим координаты точки пересечения плоскости х – 2 y + 2 z – 4 = 0 и прямой
Для этого в уравнение плоскости подставим:
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Продемонстрируем, как был получен этот результат.
x = x 1 + λ y = y 1 z = z 1
Решение
Проецирование точки в начертательной геометрии с примерами
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А:
Плоскость прямоугольника 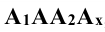
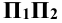
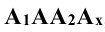
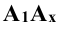
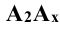
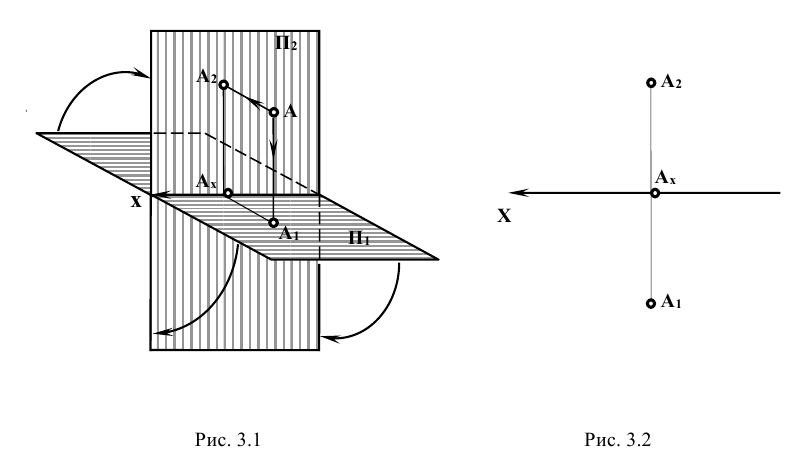
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость 
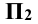
Проекции 
Для получения плоского чертежа в этом случае уже две плоскости 
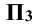
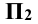
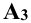
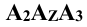
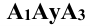
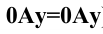
Это не означает, что модули этих величин обязательно равны между собой, т.е. 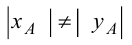
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
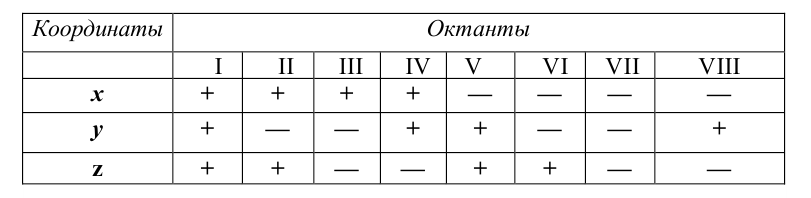
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 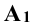
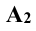
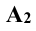
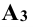
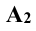
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Таблица 3.1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Проекция точки на прямую, координаты проекции точки на прямую.
В этой статье сначала дано определение проекции точки на прямую (на ось) и приведен поясняющий рисунок. Далее разобран способ нахождения координат проекции точки на прямую во введенной прямоугольной системе координат на плоскости и в трехмерном пространстве, показаны решения примеров с подробными пояснениями.
Навигация по странице.
Проекция точки на прямую – определение.
Вообще проецирование некоторой фигуры на прямую является обобщением понятия ортогонального проецирования фигуры на плоскость (смотрите статью проекция точки на плоскость).
Так как все геометрические фигуры состоят из точек, а проекция фигуры представляет собой множество проекций всех точек этой фигуры, то для проецирования фигуры на прямую необходимо уметь проецировать точки этой фигуры на данную прямую.
Так что же называют проекцией точки на прямую?
Проекция точки на прямую – это либо сама точка, если она лежит на данной прямой, либо основание перпендикуляра, опущенного из этой точки на заданную прямую.
Это определение проекции точки на прямую справедливо как для случая на плоскости, так и для случая в трехмерном пространстве.
Нахождение координат проекции точки на прямую – теория и примеры.
Начнем с нахождения координат проекции точки на прямую, когда проецируемая точка и прямая заданы в прямоугольной системе координат Oxy на плоскости. После этого покажем, как находятся координаты проекции точки на прямую в прямоугольной системе координат Oxyz в трехмерном пространстве.
Координаты проекции точки на прямую на плоскости.
Из проведенного построения логически следует алгоритм, позволяющий найти координаты проекции точки 
Разберемся с нахождением координат проекции точки на прямую при решении примера.
Уравнение прямой a нам известно из условия, так что можно переходить ко второму шагу алгоритма.
Таким образом, проекция точки 



Для нахождения координат проекции точки М1 на прямую АВ будем действовать по полученному алгоритму.
Напишем уравнение прямой, проходящей через две заданные точки 


Чтобы определить координаты проекции точки 


Какие координаты имеют проекции точки 

Проекцией точки 

Перепишем уравнение прямой 






Координаты проекции точки на прямую в трехмерном пространстве.
Рассмотрим решение примера.
Для определения координат проекции точки М1 на прямую a воспользуемся полученным алгоритмом.
Уравнения прямой a нам сразу известны из условия, так что переходим ко второму шагу.
Из канонических уравнений прямой a получим уравнения двух пересекающихся плоскостей, которые определяют прямую a:
Координаты точки пересечения прямой 


Теперь мы можем вычислить искомые координаты точки пересечения прямой a и плоскости 


То есть, проекция точки М1 на прямую a имеет координаты 

Что значит проекция точки
Образование отрезка прямой линии АА1 можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).
Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.
В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку А (рис. 85, а).
Линия пересечения плоскостей проекций — прямая, которая называется осью проекций и обозначается буквой х.
Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.
Из точки А опускают перпендикуляры на плоскости V и Н. Точки а’и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Аааха’ в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.
Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).
Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а’ — называются проекциями точки А: а’ — фронтальная проекция точки А, а — горизонтальная проекция точки А.
Линия а’ а называется вертикальной линией проекционной связи.
Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.
ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ
В тех случаях, когда по двум проекциям нельзя представить себе форму предмета, его проецируют на три плоскости проекций. В этом случае вводится профильная плоскость проекций W, перпендикулярная плоскостям V и Н. Наглядное изображение системы из трех плоскостей проекций дано на рис. 87, а.
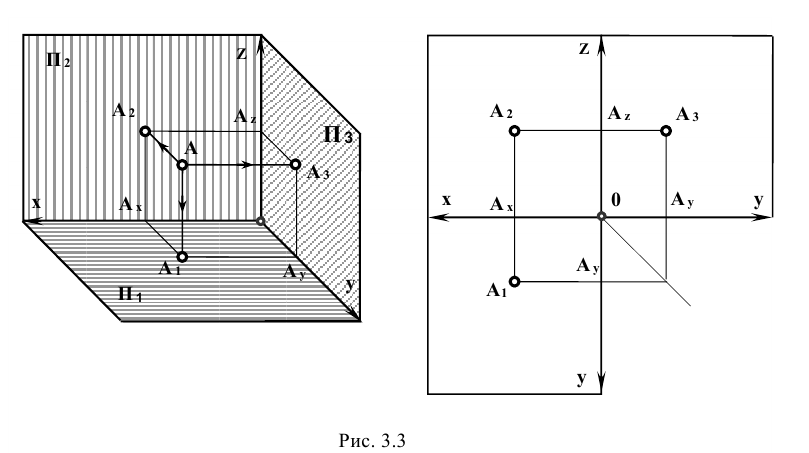
Ребра трехгранного угла (пересечение плоскостей проекций) называются осями проекций и обозначаются x, у и z. Пересечение осей проекций называется началом осей проекций и обозначается буквой О. Опустим из точки А перпендикуляр на плоскость проекций W и, отметив основание перпендикуляра буквой а», получим профильную проекцию точки А.
Для получения комплексного чертежа точки А плоскости Н и W совмещают с плоскостью V, вращая их вокруг осей Ох и Oz. Комплексный чертеж точки А показан на рис. 87, б и в.
Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются: хА, уА и zA.
Например, координата zA точки А, равная отрезку а’ах (рис. 88, а и б), есть расстояние от точки А до горизонтальной плоскости проекций Н. Координата у точки А, равная отрезку аах, есть расстояние от точки А до фронтальной плоскости проекций V. Координата хА, равная отрезку аау — расстояние от точки А до профильной плоскости проекций W.
Таким образом, расстояние между проекцией точки и осью проекции определяют координаты точки и являются ключом к чтению ее комплексного чертежа. По двум проекциям точки можно определить все три координаты точки.
Если заданы координаты точки А (например, хА=20 мм, уА=22мм и zA= 25 мм), то можно построить три проекции этой точки.
Для этого от начала координат О по направлению оси Oz откладывают вверх координату zA и вниз координату уА.Из концов отложенных отрезков — точек az и ау (рис. 88, а) — проводят прямые, параллельные оси Ох, и на них откладывают отрезки, равные координате хА. Полученные точки а’ и а — фронтальная и горизонтальная проекции точки А.
По двум проекциям а’ и а точки А построить ее профильную проекцию можно тремя способами:
1) из начала координат О проводят вспомогательную дугу радиусом Оау, равным координате (рис. 87, б и в), из полученной точки ау1 проводят прямую, параллельную оси Oz, и откладывают отрезок, равный zA;
2) из точки ау проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, а), получают точку ау1 и т. д.;
3) из начала координат О проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, б), получают точку ау1 и т. д.
Проекция точки на плоскость, координаты проекции точки на плоскость.
Эта статья является ответом на два вопроса: «Что такое проекция точки на плоскость» и «Как найти координаты проекции точки на плоскость»? Сначала дана необходимая информация о проецировании и его видах. Далее приведено определение проекции точки на плоскость и дана графическая иллюстрация. После этого получен метод нахождения координат проекции точки на плоскость. В заключении разобраны решения примеров, в которых вычисляются координаты проекции заданной точки на заданную плоскость.
Навигация по странице.
Проецирование, виды проецирования – необходимая информация.
При изучении пространственных фигур удобно пользоваться их изображениями на чертеже. Чертеж пространственной фигуры представляет собой так называемую проекцию этой фигуры на плоскость. Процесс построения изображения пространственной фигуры на плоскости происходит по определенным правилам. Так вот процесс построения изображения пространственной фигуры на плоскости вместе с набором правил, по которым осуществляется этот процесс, называется проецированием фигуры на данную плоскость. Плоскость, в которой строится изображение, называют плоскостью проекции.
В зависимости от правил, по которым осуществляется проецирование, различают центральное и параллельное проецирование. Вдаваться в подробности не станем, так как это выходит за рамки этой статьи.
Следует отметить, что проекция фигуры на плоскость представляет собой совокупность проекций всех точек этой фигуры на плоскость проекции. Иными словами, чтобы получить проекцию некоторой фигуры необходимо уметь находить проекции точек этой фигуры на плоскость. В следующем пункте статьи как раз показано, как найти проекцию точки на плоскость.
Проекция точки на плоскость – определение и иллюстрация.
Еще раз подчеркнем, что мы будем говорить о перпендикулярной проекции точки на плоскость.
Выполним построения, которые помогут нам дать определение проекции точки на плоскость.
Данному определению проекции точки на плоскость эквивалентно следующее определение.
Проекция точки на плоскость – это либо сама точка, если она лежит в заданной плоскости, либо основание перпендикуляра, опущенного из этой точки на заданную плоскость.
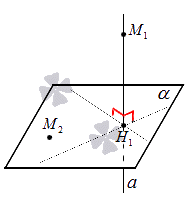
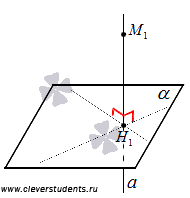
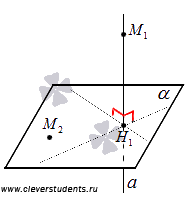
На приведенном ниже чертеже точка H1 есть проекция точки М1 на плоскость 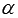
Нахождение координат проекции точки на плоскость – решения примеров.
Решение задачи логически следует из определения проекции точки на плоскость.
Рассмотрим решения примеров.
Найдите координаты проекции точки 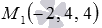
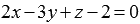
В условии задачи нам дано общее уравнение плоскости вида 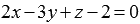
Чтобы получить требуемые координаты проекции точки на плоскость, осталось определить координаты точки пересечения прямой 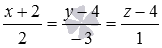
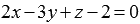
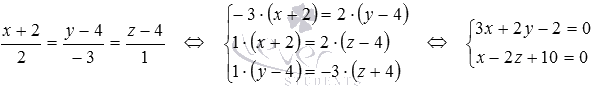
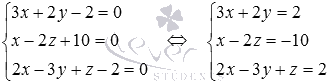
Таким образом, проекция точки 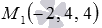
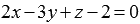
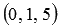
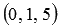
Напишем сначала уравнение плоскости, проходящей через три заданные точки 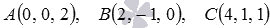
Дальше для нахождения координат проекции точки М1 на плоскость АВС можно действовать как в предыдущем примере.
Но давайте рассмотрим альтернативный подход.
Осталось определить координаты точки пересечения прямой 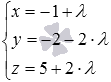
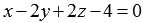
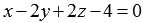
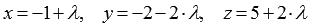
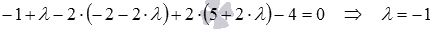
Таким образом, проекция точки М1 на плоскость АВС имеет координаты 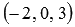
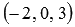
В заключении давайте обсудим нахождение координат проекции некоторой точки на координатные плоскости и плоскости, параллельные координатным плоскостям.
Покажем, как были получены эти результаты.
Для примера найдем проекцию точки 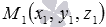
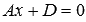
Найдем координаты точки пересечения прямой 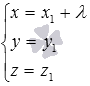
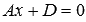
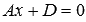
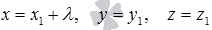
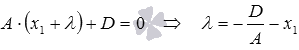
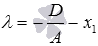
Таким образом, проекцией точки 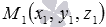

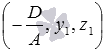
Найдите координаты проекций точки 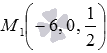
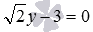
Координатной плоскости Oxy соответствует неполное общее уравнение плоскости вида 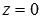
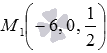
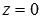
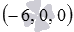
Уравнение плоскости вида