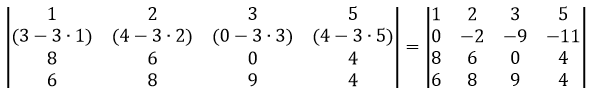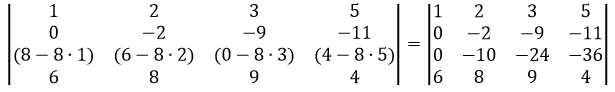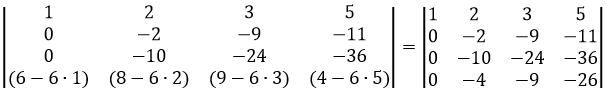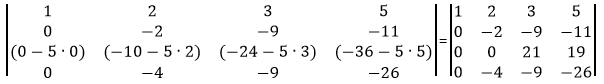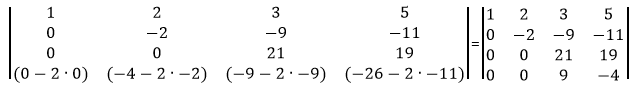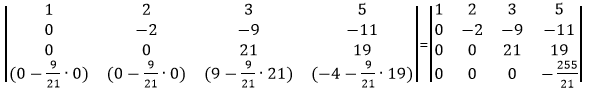Что значит привести матрицу к треугольному виду

Приведение определителя матрицы к треугольному виду

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.

Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.

Пример

Найдем определитель матрицы четвертого порядка.

Сделаем элемент a_2,1 равный нулю.

Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3

Сделаем элемент a_3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8

Сделаем элемент a_4,1 равный нулю.

Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6

Сделаем элемент a_3,2 равный нулю.

Из строки №3 вычитаем строку №2, умноженную на 5

Сделаем элемент a_4,2 равный нулю.

Из строки №4 вычитаем строку №2, умноженную на 2

Сделаем элемент a_4,3 равный нулю.

Из строки №4 вычтем строку №3, умноженную на 9/21.

Умножим элементы матрицы находящиеся на диагонали.

Источник

Приведение матрицы к треугольному виду

Приведение матрицы к треугольному виду методом Гаусса и методом Барейса.

Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.

Приведение матрицы к треугольному виду (метод Гаусса)

Приведение матрицы к треугольному виду (метод Барейса)

Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:

Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4

Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.

Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.

Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.

Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:

И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».

Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):

Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:

Зануляем во втором уравнении:

Во втором уравнении больше не содержится

Обобщенно алгоритм метода Гаусса можно представить следующим образом:

где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце

Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.

Алгоритм Барейса можно представить следующим образом:

Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).

Источник

Как привести матрицу к треугольному (ступенчатому) виду (метод Гаусса)?

Данная статья является первой частью серии статей под названием «Решение матриц». Каждая часть сопровождается теорией, примерами и подробным описанием.

Если Вам нужно привести матрицу к треугольному (ступенчатому) виду, воспользуйтесь нашим онлайн калькулятором.

Содержание:

Введение

Эту задачу приходится решать очень часто, так как она используется во многих операциях над матрицами (решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителя матрицы).

Что бы привести матрицу к треугольному виду, нужно воспользоваться методом Гаусса, который является простым в использовании и позволяет быстро прийти к конечному результату. Метод заключается в том чтобы исходную матрицу, путём элементарных преобразований привести к треугольному (ступенчатому) виду.

Описание алгоритма

Для приведения матрицы к треугольному виду, необходимо обнулить все элементы стоящие ниже главной диагонали.

Пусть дана матрица

.

Первым действием обнуляем первые элементы 2,3. n строки, для этого вычтем из этих строк первую строку умноженную на соответственно,

получим ,

где .

Теперь вычтем из 3,4. n строки вторую строку умноженную на , этим действием обнуляем вторые элементы этих строк, соответственно, получаем

,

где b_ij элементы получившиеся в результате этих преобразований. И так далее, пока не получим вид ,

где b_ij это элементы получившиеся в результате элементарных преобразований, это и есть матрица треугольного вида.

Пример приведения матрицы к треугольному виду

Заключение

Если Вам не понятен какой-либо шаг или у Вас есть вопросы по приведению матрицы к треугольному (ступенчатому) виду, вы всегда можете оставить свой комментарий ниже или решить её воспользовавшись нашим онлайн калькулятором.

Свои вопросы по данной статье, Вы всегда можете задать в комментариях.

Источник

Приведение матрицы к виду верхней треугольной «Алгоритм Барейса»

Актуальность Алгоритма Барейса

Как и вся матричная арифметика, алгоритм Барейса совершенствует (упрощает) способ обработки данных, находящихся в матрице.

Приведение матрицы к треугольному виду требуется, прежде всего, для решения систем линейных уравнений, а именно для вычисления определителя матрицы. Ведь самый быстрый способ вычислить определитель — это привести матрицу к треугольному виду (по алгоритму Гаусса), а затем перемножить её диагональные элементы.
О дополнительных преимуществах алгоритма Барейса сказано ниже…

Матрицы треугольного вида

Название говорит само за себя.

Если все элементы матрицы ниже главной диагонали равны 0, то это верхняя треугольная матрица. Если выше главной диагонали все 0, то это нижняя треугольная матрица.

Суть Алгоритма Барейса

For i = j + 1 To n
ij = mR.Cells(i, j) ‘определяем второй множитель

Где mR as Range – переменная модуля, ссылающаяся на выделенная область.

j— индексы строк, а i— индексы столбцов выделенной области.
Ячейка, обозначенная как а_-1,-1 лежит вне области выделения (т.е. выше и левее ячейки а_0,0 ) и ей в начальный период обязательно присваивается 1. В своей функции вместо а_-1,-1 я использую переменную znm (от знаменатель) и базовое значение счетчиков 1 вместо 0. Суть алгоритма это не меняет. При пошаговом выполнении программы прекрасно прослеживается постепенное приведение матрицы к верхнему треугольному виду.

Исходный код VBA EXCEL

Первую из этих функций буду использовать для проверки результата.

Источник

Методы вычисления определителей

I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.

II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.

III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.

При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.

Метод приведения определителя к треугольному виду

При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.

Итак, метод состоит из двух шагов.

1. При помощи элементарных преобразований привести определитель к треугольному виду.

2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.

Пример 2.12. Вычислить определитель четвёртого порядка

Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):

Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.

В полученной матрице нужно сделать равными нулю элементы и второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:

Получили определитель треугольного вида.

2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали :

Метод понижения порядка определителя

Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.

Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.

2. Разложим определитель по второй строке

Получили определитель третьего порядка.

Прибавим ко второму столбцу первый

Полученный определитель разложим по второму столбцу

Получили определитель 2-го порядка.

Прибавим ко второй строке первую, умноженную на (-2)

Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом

Результат совпадает с полученным в примере 2.7.

Метод изменения всех элементов определителя

При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.

Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей

отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на

Пример 2.14. Вычислить определитель n-го порядка

Решение. Рассмотрим определитель диагональной матрицы

Определитель диагональной матрицы равен произведению диагональных элементов:

Вычисление определителей с помощью рекуррентных уравнений

Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители того же вида, но меньшего порядка. Получается рекуррентное уравнение

Решая это уравнение, находим формулу, выражающую определитель через определители и порядок

В последнюю формулу подставляем определители невысокого порядка, которые нетрудно вычислить каким-либо другим способом.

Пример 2.15. Вычислить определитель n-го порядка

Решение. Разложим определитель по первой строке

Следовательно, искомый определитель удовлетворяет рекуррентному уравнению

Подберем теперь коэффициенты и в формуле так, чтобы при и она давала правильные результаты, т.е.

Пример 2.16. Вычислить определитель Вандермонда

Решение. Рассмотрим определитель

где старший коэффициент равен алгебраическому дополнению элемента

Источник