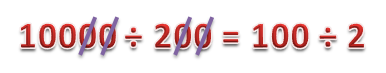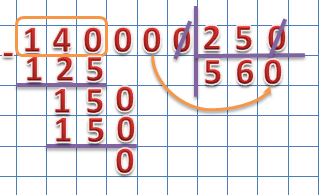Что значит первое неполное делимое
Математика. 4 класс
Конспект урока
Математика, 4 класс
Перечень вопросов, рассматриваемых в теме:
— как письменно делить трехзначные числа на однозначные?
— какой алгоритм письменного деления многозначного числа на однозначное?
Алгоритм – упорядоченный набор однозначных выполнимых шагов.
Трехзначное число – число, которое состоит из сотен, десятков и единиц первого класса.
Первое неполное делимое – это первое число, которое делится на знаменатель.
Основная и дополнительная литература по теме урока:
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с. 18, 22
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с. 46-47
4. Волкова С. И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с. 36-37
Теоретический материал для самостоятельного изучения:
Вы уже умеете делить числа в столбик. Рассмотрим теперь более сложный случай.
Фермер Василий собрал в своем саду 372 кг вишни. Он и его 3 сына поделили ягоды поровну между собой и отправились на рынок. Сколько килограммов вишни должен продать каждый член семьи?
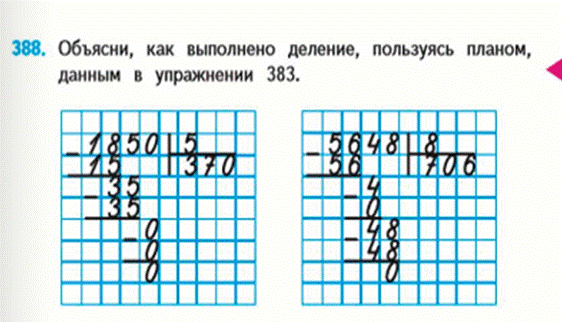
Начинаем деление с сотен. Сотен 3, но 3 сотни нельзя разделить на 4 так, чтобы в частном получились сотни. Делим десятки. Три сотни и 7 десятков – это 37 десятков. Делим 37 десятков на 4. В частном будет 9. Умножаем 9 на 4, чтобы узнать сколько десятков разделили. Получается, что разделили 36 десятков. Вычитаем из тридцати семи 36, получается 1. Значит, осталось разделить еще 1 десяток.
Переходим к делению единиц. Записываем две единицы рядом с остатком от деления десятков. 1десяток и 2 единицы – это 12 единиц. Делим 12 на 4, в частном 3. Умножаем 3 на 4, получаем 12. Вычитаем 12 из двенадцати. Осталось 0. Читаем ответ: 93.
Итак, важно запомнить: деление трехзначных чисел в столбик происходит поразрядно и начинается с высшего разряда. При нахождении каждой цифры частного, надо вспомнить три операции: деление, умножение и вычитание.
Рассмотрим еще один случай деления.
Слив фермер собрал 621 кг. Поделил их между тремя сыновьями и отправил их на рынок. Сколько килограммов слив должен продать каждый сын?
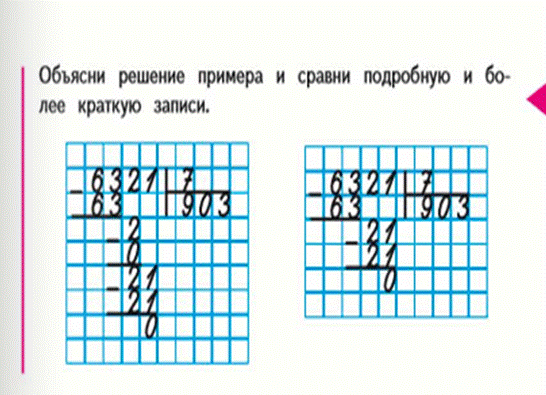
Разделим 621 на 3. Начнем деление с сотен. Делим 6 сотен на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать, сколько сотен разделили. Получается, разделили 6 сотен. Вычитаем 6 из шести, получаем 0. Значит, все сотни разделили. Ноль не пишем. Приступаем к делению десятков. Записываем 2 десятка ниже. При делении числа 2 на 3 получается 0. Умножаем 0 на 3, чтобы узнать сколько десятков разделили. Получается, что разделили 0 десятков. Вычитаем из двух ноль. Получается 2. Нам по-прежнему осталось разделить 2 десятка. Переходим к делению единиц. Записываем единицу ниже рядом с остатком 2. Два десятка и одна единица – это 21 единица. 21 делим на 3. В частном получаем 7 единиц. Умножаем 7 на 3, чтобы узнать сколько разделили единиц. Вычитаем 21 из двадцати одного, чтобы узнать остаток от деления единиц. Остаток равен 0. Читаем ответ: двести семь.
Задания тренировочного модуля:
1. Найдите значения выражения, считая устно или письменно:
выделяем первое неполное делимое (это самое малое число, начиная с высшего разряда, которое можно разделить на делитель так, чтобы получилось однозначное число не равное 0).
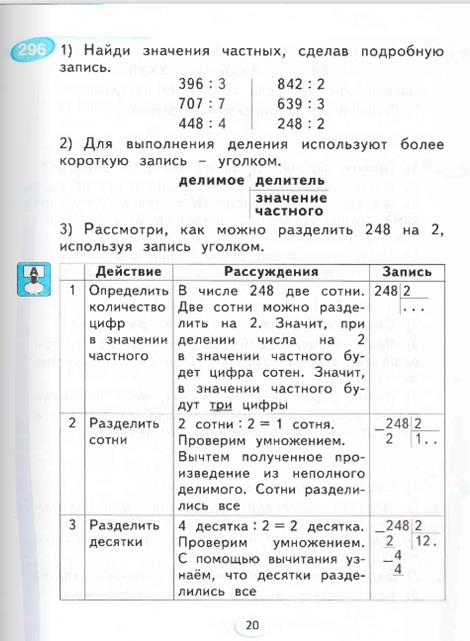
Определяем количество цифр в частном (для этого узнаем, из каких разрядных единиц состоит первое неполное делимое).
Подбираем первую цифру частного.
Узнаем, сколько единиц первого неполного делимого разделили (для этого делитель умножим на первую цифру частного).
Находим остаток, т.е. узнаем, сколько единиц первого неполного делимого не разделили.
Сравниваем остаток с делителем (если остаток меньше делителя, то цифру частного подобрали верно).
Определяем второе неполное делимое (оно состоит из остатка и единицы следующего разряда делимого) и т.д., начиная с пункта 3).
Деление выполняем до тех пор, пока не разделим единицы каждого разряда делимого.
Далее работа продолжается в концентре «Миллион».
Показываем, как использовать этот алгоритм при делении многозначных чисел на однозначное число.
М4М ч.1 с.81-83 и частные случаи с нулями с.85-87
М4М, ч.1 стр. 82
По аналогии происходит обычное деление многозначного на однозначное по первому алгоритму.
М4М, ч.1, стр. 83
Деление многозначного на однозначное, когда первое неполное делимое выражено двузначное число.
М4М,ч.1, стр. 85
1) когда на конце делимого и частного получается 0;
2) когда в середине частного получается 0.
М4М, ч.1, стр. 87
Частный случай, когда в середине частного получается 0.
Показано, как можно сократить запись при таком случае.
Рассмотрим поподробнее, как изучается прием письменного деления на однозначное число в разных учебниках математики.
Программа Н.Б. Истоминой
По программе Н.Б. Истоминой детям сначала предлагается объяснить, как выполнено деление столбиком. Затем вспоминают устный прием. Затем дается подробное объяснение приема. Также дан подробный алгоритм. Автор учебника обращает внимание детей на то, что деление в письменном приеме обозначается «уголком», а также вводится понятие «неполное делимое». Все это можно увидеть на страницах 79-83.
М4И, ч.1, стр. 79-83
В данном приеме можно выделить несколько частных случаев.
Случай, когда первое неполное делимое выражено двузначным числом
Оставшуюся единицу первого неполного делимого переводят в другой разряд
Случай с нулем в частном
Рассмотрим их поподробнее.
Далее в одном из упражнений вводят частный случай, когда в делимом нули на конце.
М4И,ч.1,стр.84
Алгоритма уже нет, предлагают детям объяснить самостоятельно.
Программа И.И. Аргинской
По программе И.И. Аргинской данный прием дети начинают изучать в 3 классе. Рассмотрим поподробнее.
М3А, ч.2, стр. 20-21
На этой странице вводится прием письменного деления на однозначное число. Затем дается тот же алгоритм, но оставшуюся единицу первого неполного делимого переводят в другой разряд – из сотен в десятки:
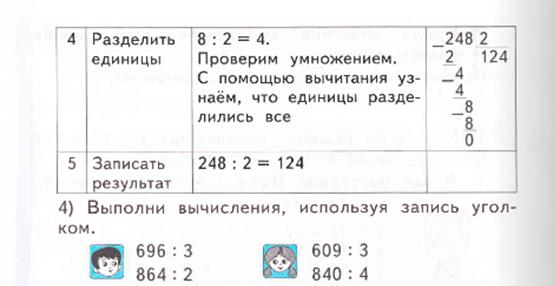
Затем дается тот же алгоритм, но оставшуюся единицу первого неполного делимого переводят в другой разряд – из сотен в десятки:
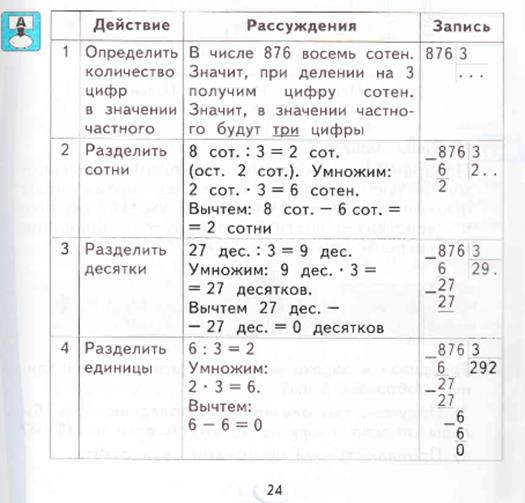
М3А, ч.2, стр.31
Частный случай деления трехзначного числа на однозначное с 0 на конце; в середине делимого.
Программа Л.Г. Петерсон
По программе Л.Г. Петерсон данный прием дети начинают изучать в 3 классе.
На странице 10 начинает новая тема «Деление на однозначное число».
На странице 11 даётся случай, когда первое неполное делимое будет двузначным.
М3П,ч.2, стр. 16
На последующем уроке рассматривается частный случай, когда в середине частного получается круглое число. 
М3П,ч.2, стр. 19
Рассматривается случай письменного деления на однозначное число, когда в конце делимого стоит 0, и в частном получается тоже в конце 0.
М3П,ч.2,стр.31
4 сотни можно разделить на 3 так, чтобы в частном получились сотни (однозначное число, отличное от 0).Значит, первое неполное делимое – 4 сотни. В частном будет три цифры, т.к. сотни стоят на третьем месте справа. Делим 4:3, возьмем по 1. Узнаем, сколько сотен разделили. Для этого 1*3=3.Узнаем, сколько сотен не разделили. Для этого из 4 – 3=1 сотня. Сравним остаток с делителем, 1
Как найти первое неполное делимое и количество цифр в частном?
В самом начале обучения навыку деления чисел дети часто допускают ошибки. Одними из самых распространенных, помимо ошибок непосредственно в совершении промежуточных вычислений, являются появление «лишних» цифр и потеря нулей в частном. Их возникновение зачастую связано с такими причинами:
Этой статьей я хочу помочь школьникам восполнить пробелы в вышеупомянутых базовых знаниях, чтобы в дальнейшем они смогли избегать ошибок при совершении действия деления в столбик.
Как найти первое неполное делимое?
Рассмотрим подробно по шагам на таком примере \( <\color
1. Смотрим, сколько разрядов в делимом и какая цифра стоит на позиции самого старшего разряда этого числа.
1. 1. Проверяем, можно ли это количество единиц этого разряда разделить на делитель так, чтобы получилось натуральное число?
1. 2. Если разделить нельзя, смотрим на количество единиц следующего разряда и проверяем, можем ли мы их разделить на делитель?
В числе 75184 всего 75 единиц разряда тысяч. 75 тысяч можно разделить на 12 – получится 6 полных тысяч, и 3 тысячи неразделенные.
2. Если можно разделить количество единиц разряда на делитель, то это количество единиц и будет первым неполным делимым.
В нашем примере это 75 тысяч.
Каждая оставшаяся цифра делимого будет участвовать в формировании остальных неполных частных, о чем подробно рассказано в уроке Деление натуральных чисел.
Как найти количество цифр в частном?
Так как первое неполное делимое в данном примере – это 75 тысяч, то есть, мы делим единицы тысяч, тогда самый старший разряд частного также будет тысячи. Значит, помимо цифры самого большого разряда, будут ещё три цифры: в сотнях, десятках и простых единицах.
Итак, чтобы узнать количество цифр в частном, нужно:
1. Найти первое неполное делимое.
2. Посчитать, сколько в делимом остальных цифр.
3. Прибавить к этому количеству единицу (цифра частного, полученная после деления первого неполного делимого).
4. Результат и будет количеством цифр в частном.
Поделим, и убедимся:
В конце хочу сказать, что определение количества цифр в частном помогают развить и укрепить очень необходимый для младших школьников навык – самоконтроль.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3 / 5. Количество оценок: 17
интернет проект BeginnerSchool.ru
Сайт для детей и их родителей
Деление в столбик
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
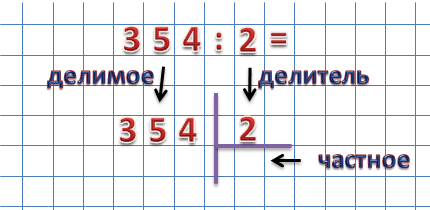
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
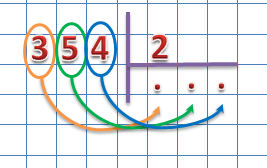
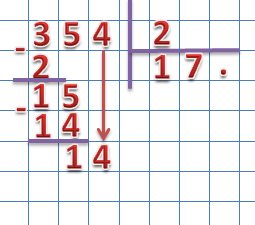
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
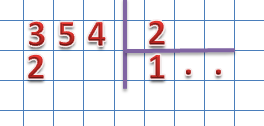
2 × 1 = 2 (2 3)
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
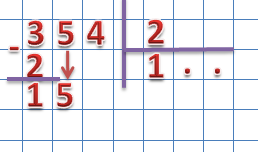
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
2 × 7 = 14 (14 15)
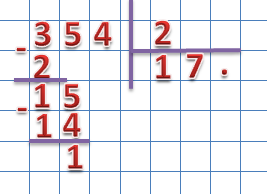
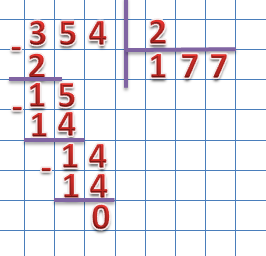
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
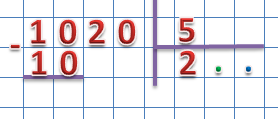
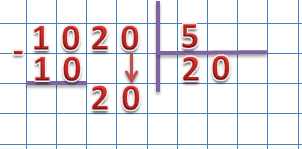
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
10 – 10 = 0
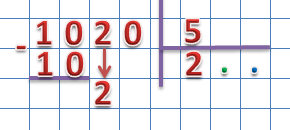
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
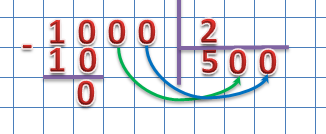
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Спасибо, что вы с нами.
Оставляйте пожалуйста комментарии в форме ниже