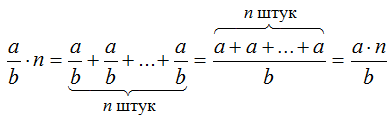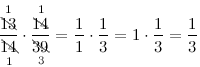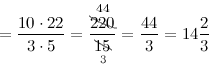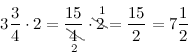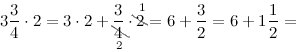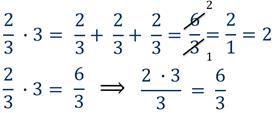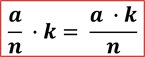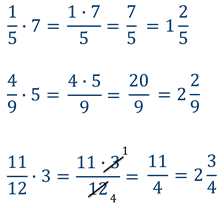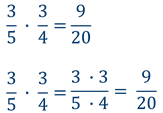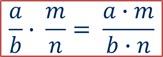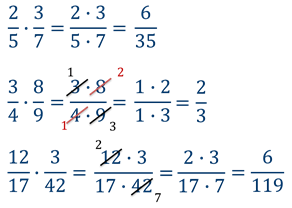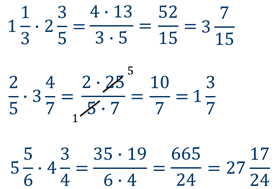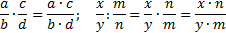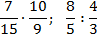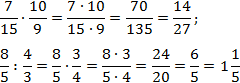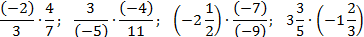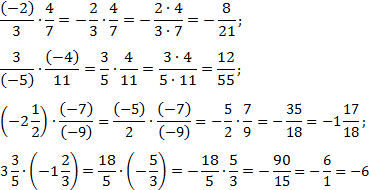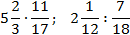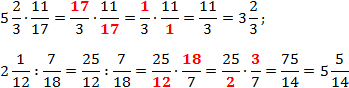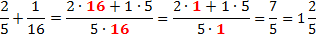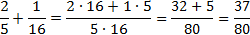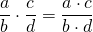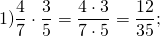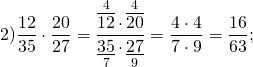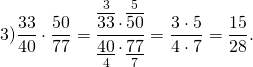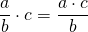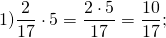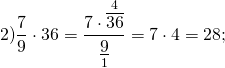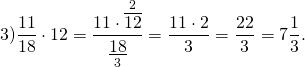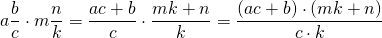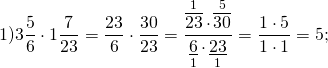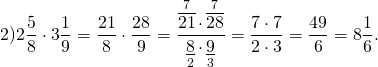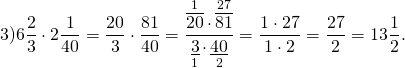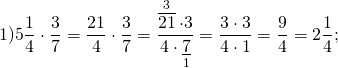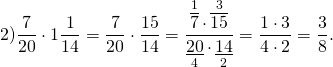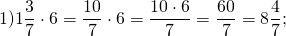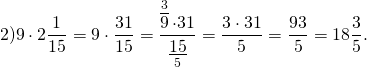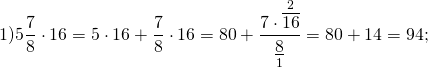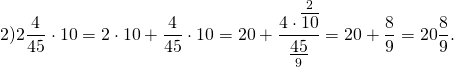Что значит перемножить дроби
Умножение дробей
Умножение дроби на число
Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой дроби умножить на это число, а знаменатель оставить без изменения.
Решение. Выполним умножение по описанному выше правилу
Аналогично выполняется умножения числа на дробь.
Умножение дробей не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти произведение 3$\cdot \frac<1><4>$
Решение. Выполним умножение по описанному выше правилу
Умножение дробей
Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.
Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.
Решение. Выполним умножение дробей по описанному выше правилу
Умножение смешанных дробей
Чтобы перемножить смешанные дроби, нужно представить их в виде неправильных дробей, а затем уже выполнить умножение как обыкновенных дробей.
Задание. Найти произведение дробей 3$\frac<1> <3>\cdot 4 \frac<2><5>$
Решение. Выполним умножение смешанных дробей по описанному выше правилу
Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число, либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.
Задание. Умножить смешанную дробь 3$\frac<3><4>$ на 2
Решение. Выполним умножение смешанной дроби на число по описанному выше правилу
Умножение дробей
Урок 13. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Умножение дробей»
На этом уроке мы разберёмся, как умножают обыкновенные дроби. Выведем правила умножения обыкновенных дробей на натуральные числа, умножения обыкновенных дробей на обыкновенные дроби и умножения смешанных чисел.
Из этой записи нетрудно заметить, что числитель дроби умножили на натуральное число, а знаменатель оставили таким же.
Запишем правило умножения обыкновенных дробей на натуральное число:
Чтобы умножить дробь на натуральное число, нужно на это число умножить числитель, оставив неизменным знаменатель.
В буквенном виде это правило можно записать так:
Длина прямоугольника 

А теперь попробуем вывести правило умножения обыкновенных дробей. Смотрите, как получили числитель и знаменатель. Видно, что числитель первой дроби умножили на числитель второй дроби, аналогично и со знаменателями. Знаменатель одной дроби умножили на знаменатель второй дроби.
Следовательно, отсюда правило умножения обыкновенных дробей:
Чтобы умножить дробь на дробь, нужно отдельно перемножить их числители и их знаменатели и первый результат записать числителем, а второй знаменателем.
Или короче можно сказать так: чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель умножить на знаменатель.
В буквенном виде это правило можно записать так:
Мы научились умножать дробь на натуральное число, дробь на дробь. Осталось разобраться, как умножают смешанные числа.
Следовательно, запишем правило умножения смешанных чисел:
Чтобы перемножить смешанные дроби, нужно сначала преобразовать их в неправильные дроби, а затем выполнить умножение дробей.
Умножение дробей имеет переместительное и сочетательное свойства, а также распределительное свойство относительно сложения и вычитания.
Справедливы также свойства нуля и единицы при умножении.
Чтобы умножить дробь на натуральное число, можно на это число умножить числитель, оставив неизменным знаменатель.
Чтобы умножить дробь на дробь, нужно отдельно перемножить их числители и их знаменатели и первый результат записать числителем, а второй знаменателем.
Чтобы перемножить смешанные дроби, нужно сначала преобразовать их в неправильные дроби.
Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Задача. Найдите значение выражения:
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Умножение и деление алгебраических дробей
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
2 3 · 4 7 = 2 · 4 3 · 7 = 8 21
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
2 3 : 7 11 = 2 3 · 11 7 = 22 7 = 1 1 21
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a · b + 1 a 3 дробь a 3 a · b + 1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1 x + y · 3 · x · y x 2 + 5 = 1 · 3 · x · y ( x + y ) · ( x 2 + 5 )
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1 · 3 · x · y ( x + y ) · ( x 2 + 5 ) = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x 2 + 5 3 · x · y :
1 x + y : 3 · x · y x 2 + 5 = 1 x + y · x 2 + 5 3 · x · y
Приведем полученную дробь к стандартному виду:
1 x + y · x 2 + 5 3 · x · y = 1 · x 2 + 5 ( x + y ) · 3 · x · y = x 2 + 5 3 · x 2 · y + 3 · x · y 2
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
У нас получилась дробь, которую можно сократить:
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
Вот запись всего решения без пояснений:
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
Как умножить или разделить алгебраическую дробь на многочлен
Решение
Начнем с замены многочлена дробью, далее действуем согласно основному правилу.
Умножение дробей
Умножение дробей — тема, включающая в себя действия с обыкновенными дробями, смешанными числами, десятичными дробями.
Запишем на одной странице все правила, касающиеся умножения обыкновенных дробей, смешанных и натуральных чисел.
Чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель — на знаменатель.
Произведение числителей записывают в числитель, знаменателей — в знаменатель. Если возможно, дроби следует сократить. Проще сокращать множители, чем результат.
Примеры умножения обыкновенных дробей :
Чтобы умножить обыкновенную дробь на натуральное число, надо числитель умножить на это число, а знаменатель оставить тем же.
Если возможно, дробь следует сократить. Если в результате получили неправильную дробь, нужно выделить из неё целую часть.
Примеры умножения обыкновенной дроби на натуральное число :
Чтобы умножить смешанные числа, надо перевести их в неправильные дроби и применить правило умножения обыкновенных дробей.
Примеры умножения смешанных чисел :
Примеры умножения смешанного числа и обыкновенной дроби :
1) Чтобы смешанное число умножить на натуральное, можно смешанное число перевести в неправильную дробь и применить правило умножения дроби на натуральное число.
Примеры умножения смешанного числа на натуральное число по первому правилу :
2) Чтобы умножить смешанное число на натуральное, можно отдельно умножить на это число целую часть, отдельно — дробную, и полученные произведения сложить.
Примеры умножения смешанного и натурального чисел по второму правилу :
В следующий раз рассмотрим все правила, касающиеся умножения десятичных дробей.