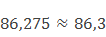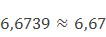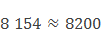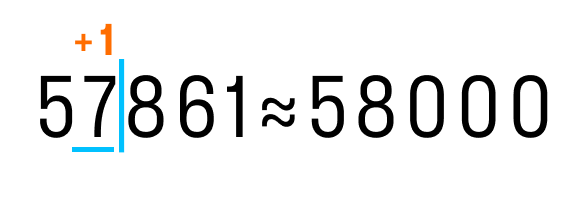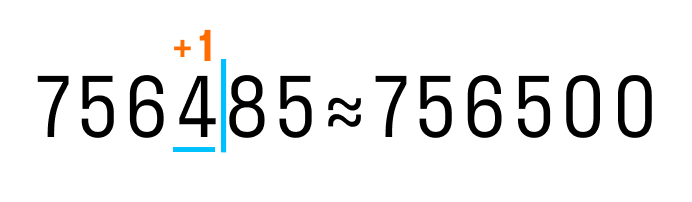Что значит округление с недостатком и с избытком
Что значит округление с недостатком и с избытком
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В жизни человека встречается два вида чисел: точные и приближённые.
Например, у квадрата четыре стороны, число 4 является точным.
Другая ситуация, на вопрос, сколько вам лет вы отвечаете 12, это приближенная величина, мы ведь не говорим 12 лет 7 месяцев 26 дней.
На практике мы часто не знаем точных значений величин. Никакие весы, как бы хорошо они ни были настроены, не могут показать абсолютно точный вес. Любой термометр показывает температуру с той или иной погрешностью. Наш глаз не в состоянии увидеть четко показания прибора, поэтому вместо того, чтобы иметь дело с точным значением величины, мы вынуждены оперировать с ее приближённым значением
Однако знание о приближённом числе уже даёт понимание о сути дела, и к тому же не всегда точное значение бывает необходимо.
Приближенные значения чисел в математике разделяют на:
1. приближенные значения с избытком;
2. приближенные значения с недостатком.
Например, про арбуз, который весит 9 кг 280 г, мы можем сказать, что его вес примерно равен 9 кг. Это приближенное значение с недостатком. А если бы его вес составлял 9 кг 980 грамм, мы бы сказали 10 кг – это приближенное значение с избытком.
Давайте рассмотрим такие примеры:
1)число 58,79 больше чем 58, но меньше 59. Число 58,79 ближе расположено к натуральному числу 59;
2)число 181, 123 больше, чем 181, но меньше, чем 182. Число 181,123 расположено ближе к натуральному числу 181. То натуральное число, к которому дробь ближе называют округленным значением этого числа.
Под округлением числа понимают отбрасывание одной или нескольких цифр в десятичном представлении числа. Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Например, число 58,79 округляется до 59, так как число 59 расположено ближе, а число 181,123 округляется до 181.
А что делать, если расстояния до приближенного значения числа с недостатком и избытком равны, например, 23,5? Оказывается, округляют в большую сторону! Т.е. получится 24
Наверняка у вас возник вопрос: «А можно ли округлять не до целого?» Конечно! Округлять можно и до других разрядов, например, до десятых, сотых, тысячных или же до десятков, сотен, тысяч и так далее.
Существует четкое правило для округления чисел:
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если за подчеркнутой цифрой стоит цифра 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.
Теперь стало понятно, почему число 23,5 округлили до 24.
Т.к. отбрасываемая цифра равна 5.
Округлим число 86,275 до десятых.
Подчеркнем цифру 2, отбрасываем цифры 7 и 5, которые следуют за разрядом десятых. За подчеркнутой цифрой 2 стоит цифра 7, поэтому цифру 2 увеличиваем на 1. Получаем 86,3. Записывают это так:
Округлим число 6,6739 до сотых.
Подчеркиваем цифру 7, отбрасываем цифры 3 и 9, которые следуют за разрядом сотых. За подчеркнутой цифрой 7 стоит цифра 3, поэтому цифру 7 оставляем без изменения. Получаем 6,67.
Записывают это так:
Таким образом, можно убедиться, что если десятичную дробь округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры отбрасывают.
Округлим число 8 154 до сотен.
Подчеркиваем цифру 1, за ней следует цифра 5, значит 1 заменяем цифрой 2, а все последующие цифры нулями, то есть получится 8200.
Записывают это так:
Делаем вывод, что при округлении натурального числа до некоторого разряда все цифры последующих разрядов заменяются нулями.
Итак, перед вами несложный алгоритм, который позволяет правильно выполнить округление любого числа:
Первое: найти нужный разряд и подчеркнуть стоящую в нем цифру.
Второе: переписать все цифры, стоящие до нее.
Третье: заменить все цифры, стоящие после выделенной, нулями до конца целой части или отбросить все цифры, имеющиеся после выделенной, если они стоят после запятой.
Четвертое: увеличить выделенную цифру на единицу, если за этой цифрой стоит цифра 5,6,7,8,9 или переписать выделенную цифру без изменений, если за ней стоит цифра 0,1,2,3,4.
Таким образом, в ходе этого урока Вы узнали, что такое приближенные значения чисел с недостатком и избытком округление чисел, а также приобрели четкий алгоритм, который позволяет правильно выполнить округление любого числа!
Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535. Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213. то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
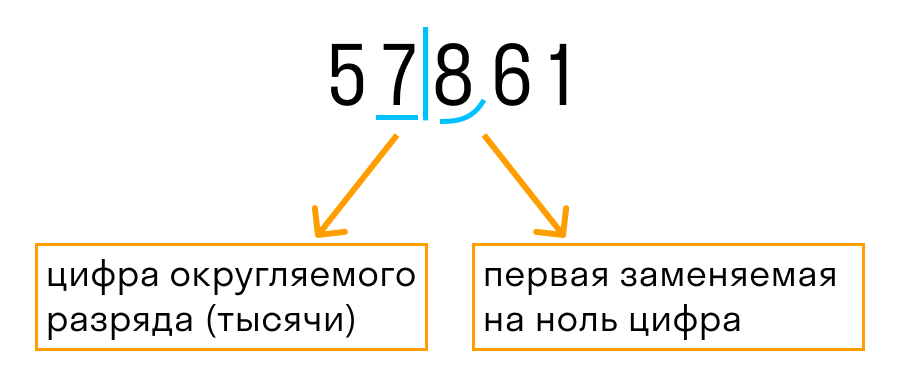
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
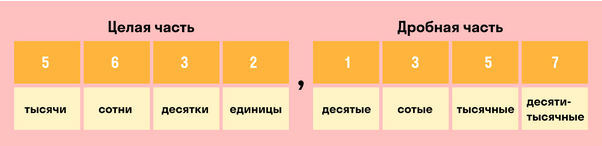
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
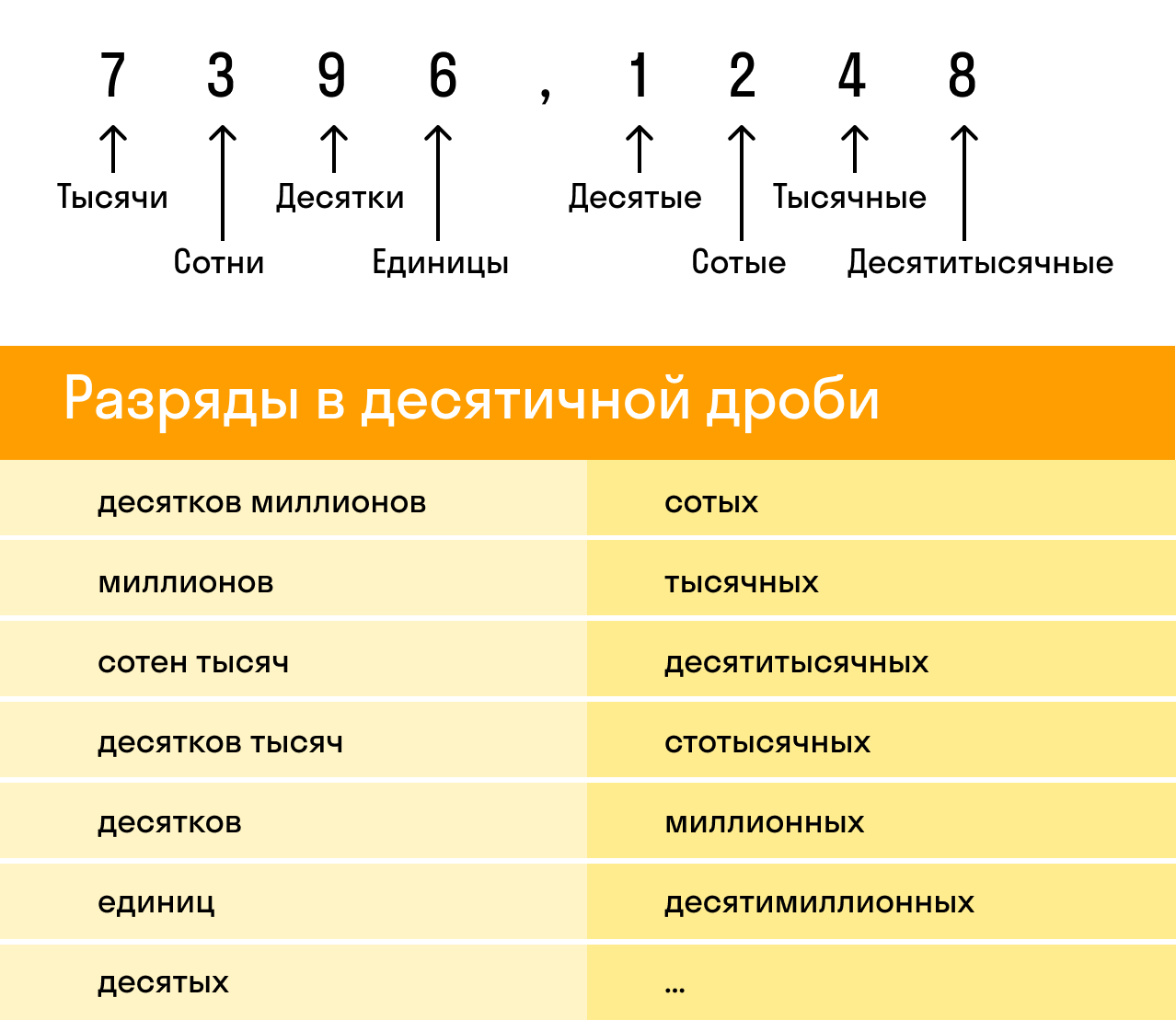
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Округление десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
Еще одно правило округления, которое нужно запомнить
Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.
Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.
Примеры округления десятичной дроби
Давайте разберем несколько примеров округления дробной части десятичных дробей.
Пример 1. Округлите дробь 56,786 до сотых.
Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.
Справа от цифры округляемого разряда цифра 6.
Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.
Пример 2. Округлите дробь 0,647 до десятых.
Округляемая цифра — 6.
Смотрим пункт 3. Значит, цифра 6 остается неизменной.
Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.
Цифра, которую нужно округлить, — 3.
Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 4. Округлите дробь 3,286 до десятых.
Цифра, которую нужно округлить, — 2.
Согласно правилу, прибавляем: 2 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 5. Округлите дробь 45,387 до сотых.
Затем отбрасываем все остальные цифры, стоящие справа.
Конспект урока математики в 4 классе «Округление с недостатком и с избытком»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику


Тема: Округление с недостатком и с избытком
Цель урока : создать условия для формирования умения проводить обобщение на
основе анализа и представлять сделанные выводы в виде схемы ( познавательные УУД ).
познакомиться с понятиями «округление с недостатком», «округление с избытком»;
проводить округление чисел с заданной точностью;
решать задачи на нахождение средней величины.
Оборудование: И.И.Аргинская, Е.И.Ивановская, С.Н.Кормишина «Математика 4 класс» 1 часть, 2012 г., Е.П.Бененсон, Л.С.Итина «Математика 4 класс» рабочая тетрадь, часть 1, 2012г., тетради, ручки, смайлики, проектор, экран, карточки для групповой работы.
Проверка домашнего задания.
— Начнём урок математики с проверки домашнего задания. Прочитаем его.№101 стр.53 Е.Н.Бененсон, Л.С.Итина Рабочая тетрадь.
— Кто такой Рене Декарт? (Французский математик, живший в 16-17 веках)
— Какие закономерности подметили, выполняя это задание?
— если хотя бы один множитель увеличивается, то и значение произведения увеличивается.
-Какие высказывания французского математика Рене Декарта вы расшифровали?
«МОЖНО УСТУПИТЬ СИЛЕ, НО БЕЗРОПОТНО ПОКОРЯЮТСЯ ТОЛЬКО РАЗУМУ».
— А какие пословицы про разум вы ещё помните?
Ум да разум надоумят сразу.
Ум разуму подспорье.
Где ума не хватит, спроси у разума.
Добрый разум наживают не разом.
При разумном деле и голову уважают.
Ум без разума беда.
— Мало иметь хороший ум, главное – хорошо его применять.
Рене Декарт говорил: « Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать»
Сегодня на уроке вам предоставится такая возможность.
Давайте начнём размышлять.
На доске числа: 128, 4, 233, 56, 354, 32, 121.
-Что вы можете сказать об этих числах?
-Натуральные, есть чётные и нечётные, многозначные и однозначное, не круглые.
-Какое задание вы могли бы предложить с этими числами?
-Составить выражение и найти значение
— Разделить на 2 группы. (чётные и нечётные)
— Разделить на 3 группы. (однозначные, двузначные, трёхзначные)
-Здесь есть числа, связанные между собой – 128:4=32, 354-121=233
(запись в тетрадях выражений)
-Вы точно знаете, что значение 32 и 233?
-Значит это точные числа. А какие ещё бывают числа?
-Ещё бывают приближённые числа.
— А что вы знаете о приближённых числах?
— В результате измерений получают приближенные значения длины, массы, площади и т.д., а в процессе подсчета количества, чаще всего, точные данные.
— Скажите, пожалуйста, где в жизни мы сейчас встречаемся с приближенными числами?
— В жизни мы часто имеем дело с приближенными значениями. Иногда просто невозможно точно сосчитать, а иногда не нужно точно знать, сколько чего либо. Например: всего на планете живет около 350 тысяч видов растений;
— В словаре русского языка Ожегова на титульном листе указано, что в нем около 57 000 слов (хотя можно было бы подсчитать их точное количество).
— В магазине на ценнике написано 10 руб. 17 коп., а мы отдаем 10 р. 20 коп.
Например, взвесили курицу, ее вес 1 кг 357 г, но продавец скажет: вес курицы 1 кг 360 г. Он округлил.
А что значит округлить?
Я думаю, что мы должны назвать такое число, в котором последняя цифра нуль.
Я сегодня по дороге в школу купила 2 пакета молока.( Работа в группах. У мальчиков пакет с молоком красного цвета, у девочек – синего)
Когда мы покупаем что-либо из продуктов питания, на какие числа мы обращаем внимание?
Дата выпуска и конца реализации. Это важно для здоровья.
Почему пакеты разного цвета?
Разный %жирности. 2,5% и 3,2%
Что можете сказать об этих числа?
В Чувашии хорошо развита молочная промышленность. Найдите на пакетах производителя.
Чебоксарский молочный завод.
А ещё молочные заводы есть в Ибресях, Янтиково, Ядрине, Цивильске.
Итак, приближённые значения чисел получаются, когда мы округляем числа. А для чего нужно округлять?
Числа округляют, когда полная точность не нужна или невозможна
2) Работа в группах на карточках:
— На первой карточке приближённые значения получились меньше данных чисел, а на второй – больше.
-А почему? Подумайте. Какие цифры в первом числе заменяли нулями?
— Какие цифры заменяли во втором числе?
3) Постановка темы и задач урока
— Попробуйте сформулировать тему нашего урока и главную задачу.
— Округление с недостатком и с избытком.
— Научиться различать округление с недостатком и с избытком.
— Научиться округлять с недостатком и с избытком.
— Давайте прочитаем, что сказано об этом в учебнике. Стр. 94 №185
4) Применение нового знания с опорой на схему.
-А как бы вы округлили число 55 555 с точностью до любого разряда?
Чтение правила в учебнике. Как теперь изменится схема в учебнике?
0,1, 2, 3, 4 5 6, 7, 8, 9
5.Закрепление нового знания.
Округление до сотен: до тысяч:
931 ≈ 900 5 972 ≈ 6000
45 365 ≈ 45370 14013 ≈ 14000
9 423 ≈ 9400 873 478 ≈ 873000
78 089 ≈ 78100 405 076 ≈ 405000
— Скажите, ребята, а ваш рост – это точное число или приближённое?
-Приближённое, т.к. измеряется прибором – ростомером.
Правильно, ведь вы постоянно растёте.
Давайте покажем как вы росли?
( под музыку Карена Саркисяна дети из положения сидя, обхватив колени, медленно приподнимаются, туловище выпрямляется.
Учитель сообщает сведения:
от одного до трех лет скорость роста ребенка составляет от 7,5 до 13 см в год. Затем скорость роста постепенно снижается, и в 3–4 года ребенок вырастает на 0,5 см в месяц.
6) Решение задачи №186.(нахождение среднего арифметического)
-А что ещё может расти? (растения)
— Поднимите руки те, у кого дома весной мамы или бабушки сеют семена огурцов в ящики. Все ли семена дают всходы?
Вот и в задаче тоже взошли не все семена. Прочитайте №186.
Давайте составим краткую запись.
— Как найти среднее значение?
— Надо сложить все числа, затем значение суммы разделить на количество слагаемых.
Ответ: 93 семечка в среднем взошли.
—Как изменение одного слагаемого в сумме 1 действия влияет на результат задачи.
-Если в пятом ящике взойдет на 5 семян меньше, то в значении суммы в первом действии также станет на 5 меньше, а результат второго действия на 1 меньше.
— Какую задачу мы ставили по теме урока?
— Когда округляем с избытком? А когда с недостатком?
— Кто понял тему урока? (Поднимают смайлик с улыбочкой)
— Кто ещё сомневается, что он понял? (Поднимают грустный смайлик)
— Вы очень старались на уроке, хорошо размышляли, и поэтому, я думаю, сегодня за урок вы смогли усовершенствовать свой ум. А разум подскажет, как применить новые знания во благо.
5. Домашнее задание: №188 стр. 96
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: 54282040122
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В Москве новогодние утренники в школах и детсадах пройдут без родителей
Время чтения: 1 минута
Госдума приняла закон об использовании онлайн-ресурсов в школах
Время чтения: 2 минуты
Псковских школьников отправили на дистанционку до 10 декабря
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Трехлетнюю олимпиаду среди школ запустят в России в 2022 году
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.