Что значит однородная величина

Свойства однородных величин

1. Однородные величины можно сравнивать. Для любых величин А и В справедливо только одно из отношений: А В, А=В.

Например, масса книги больше массы карандаша, а длина ка­рандаша меньше длины стола.

2. Однородные величины можно складывать и вычитать. В резуль­тате получается величина того же рода.

Величины, которые можно складывать, называются аддитивны­ми. Например, можно складывать длины предметов. В результате получается длина. Существуют величины, которые не являются ад­дитивными, например температура. При соединении воды разной температуры из двух сосудов получается смесь, температуру которой нельзя определить сложением величин.

Мы будем рассматривать только аддитивные величины.

Пусть: А — длина ткани,

В — длина куска, который отрезали, тогда;

3. Величину можно умножать и делить на положительное дей­ствительное число. В результате получается величина того же рода.

2) «Раздели ленту на 4 равные части». Если длина ленты — L, то длина каждой ее части — L.4.

4.Однородные величины можно делить. В результате получается положительное действительное число, его называют отношением ве­личин. А:В=х о А—В-х.

5. Величину можно оценить количественно, то есть измерить.

Дети уже в дошкольном возрасте учатся выделять разные пара­метры размера предмета (длину, ширину, высоту), сравнивать пред­меты по этим параметрам (наложением и приложением), измерять протяженность условными мерками. Довольно рано происходит знакомство с площадью фигур, объемом жидких и сыпучих веществ, массой физических тел, промежутками времени. В быту дети накап­ливают необходимый опыт для последующего обучения, системати­зации и расширения знаний. Измерительная деятельность формиру­ется только под воздействием целенаправленного обучения. В на­чальной школе происходит знакомство с общепринятыми единицами величин (метром, литром, килограммом и др.).

Измерение величин

Сравнивая величины непосредственно, можно установить их равенство или неравенство.

Для получения более точного результата сравнения величины измеряют. Например, измеряя массу арбуза на чашечных весах, сравнивают ее с массой гири. Измеряя длину комнаты шагами, сравнивают ее с длиной шага.

Процесс сравнения зависит от рода величины: длину измеряют с помощью линейки, массу — используя весы. Каким бы ни был этот процесс, в результате измерения получается определенное чис­ло, зависящее от выбранной единицы величины.

Измерение заключается в сравнении данной величины с некото­рой величиной того же рода, принятой за единицу.

Цель измерения — получить численную характеристику данной величины при выбранной единице величины.

Измерить величину А — это значит найти такое положительное действительное число х, что А=х Е, где Е — величина того же рода, принятая за единицу. Число х называют численным значением вели­чины А при единице величины Е.

Численное значение величины показывает, во сколько раз за­данная величина больше или меньше величины, принятой за еди­ницу.

1) Если масса дыни 3 кг, то 3 — численное значение массы дыни при единице массы килограмм.

Величины, определяемые одним численным значением, называ­ются скалярными (длина, объем, масса и др.). Существуют еще век­торные величины, которые определяются численным значением и направлением (скорость, сила и др.). Мы будем рассматривать толь­ко скалярные величины (длину, площадь, объем, массу, время).

Значение измерения очень велико. Не всегда можно сравнить или сложить (вычесть) величины непосредственно (например, дли­ну дорог). Измерение позволяет свести сравнение величин к сравне­нию чисел, а действия с величинами — к действиям над числами, что значительно проще.

Источник

Измерение величин и именованные числа

С начала 5 класса мы с вами изучали только натуральные числа. Они исторически появились первыми как результат удовлетворения потребности человека в более удобном и качественном счете предметов. Но уже в те далекие времена люди поняли, что не все можно посчитать только такими числами, которые мы сегодня называем натуральные.

Поэтому, таким же естественным путем, каким были введены в жизнь человека натуральные числа, произошло появление дробных и смешанных чисел, речь о которых пойдет в следующих уроках. Этот же урок рассматривает одно из важнейших человеческих действий, которое напрямую привело к необходимости введения нового огромного класса чисел.

Измерение величин

Давайте представим, что нам нужно определить точное расстояние, к примеру, от одного конца комнаты до другого, то есть, узнать длину комнаты. Мы, конечно, можем при достаточных усилиях сделать это так, как в мультфильме «38 попугаев» – посчитать ее в мартышках, попугаях или слонятах. Но если мы так поступим, то мы не сможем сделать так, чтобы нас поняли другие, потому что размеры этих животных могут быть разные, и у каждого могут быть свои представления о них. Не водить же зверей все время с собой?

Единица измерения какой-либо величины – это известная всем величина, которая принята в качестве основной меры для измерения других величин этого же рода.

Измерить величину – это означает определить, какое количество единиц измерения содержится в этой величине.

Можно выразить это определение более обобщенно.

Измерить величину – это означает определить, какое количество известных величин этого же рода, принятых в качестве единицы измерения, содержится в этой величине.

Меры измерений величин

Однородные меры – это такие меры, которые применяются для измерения однородных величин.

Отношение однородных мер – это показатель, который равен количеству меньших мер, содержащихся в большей мере. Иными словами, сколько раз можно в большей мере поместить меньшую.

Например, отношение сантиметра к миллиметру – это число 10.

Метрическая система мер

Меры длины

Соотношения величин вы можете всегда посмотреть в справочнике.

Кроме этого, метр также собирается в более крупные меры, по 10 более мелких частей в каждой. 10 метров – это декаметр (произошло от древнегреческого δέκα – десять), 100 метров – гектометр (древнегреческого ἑκατόν – сто), 1000 метров – километр (от древнегреческого χῑλιάς – тысяча).

Меры площади

Так, один квадратный метр – это площадь квадрата, у которого сторона равна 1 метру, один квадратный километр – это площадь квадрата с длиной стороны 1 километр.

Одна квадратная мера площади состоит из 100 мер более низкого соседнего с ней разряда.

Для обозначения площадей полей и лесов применяют два особых названия.

Меры объема

Одна кубическая мера объема состоит из 1000 мер более низкого соседнего с ней разряда.

Меры веса

Конечно, с точки зрения физики правильно говорить масса, а не вес. Но мы используем эти слова в повседневном обиходе как синонимы, поэтому и я допускаю подобную трактовку в своих уроках математики.

Кроме этих мер свои названия имеют и более крупные группировки: в 1 центнере находится 100 килограмм, а в 1 тонне – 1000 килограмм.

Меры объема жидкостей

Литр – это объем, который заполняет один килограмм воды при определенных условиях: нормальное атмосферное давление и максимальная плотность воды.

10 литров составляют 1 декалитр, 100 литров образуют гектолитр, 1000 литров – 1 килолитр.

Единицы измерения времени

Существуют две основные меры времени.

Сутки – это величина времени, приближенно равная одному обороту нашей планеты Земля вокруг своей оси.

Год – это такая величина времени, которая приближенно равна одному полному обороту Земли вокруг Солнца.

Часы в сутках считают сразу от 1 до 24, или разбивают на две части по 12 часов и считают от 1 до 12 (до полудня), а затем опять от 1 до 12 (уже до полуночи). При этом для уточнения периода суток добавляют: «до полудня», «после полудня» или указывают: «ночи», «утра», «дня» или «вечера».

Так, 15 часов – это 3 часа после полудня, или просто 3 часа дня, а 22 часа – это 10 часов после полудня, или 10 часов вечера.

Про год и летоисчисление вы узнаете больше из этой статьи.

Именованные числа

Именованное число – это числовое выражение величины измерения совместно с указанием единиц измерения этой величины.

Отвлеченное число – это просто число без указания единицы измерения какой-либо величины.

Например, 12 деревьев, 3 килограмма, 135 литров – это именованные числа, а 12, 3 и 135 – отвлеченные.

Именованное число может состоять только из одной меры : 18 л, 312 км, 48 г, или из нескольких, но обязательно однородных: 5 кг 640 г, 12 м 72 см.

Нельзя в одном именованном числе смешивать меры разных величин, например, так: 12 кг 58 см или 15 л 12 г.

Простое именованное число – имеет в своем составе только одно наименование какой-либо величины.

Составное именованное число выражается несколькими единицами измерения одной и той же величины.

Именованные числа можно преобразовывать в более крупные или мелкие наименования однородных мер, то есть, увеличивать или уменьшать их разряд.

Превращением или укрупнением именованного числа называется его преобразование в более крупное наименование однородной меры.

Раздроблением именованного числа называется его преобразование в более мелкие единицы однородной меры.

Так, записав именованное число 5203 метра как 5 км 203 м, мы совершили превращение, а преобразовав 5 км 203 м в 5203 м, – раздробление.

Источник

Понятие величины, свойства однородных величин

Этапы исторического развития способов измерения величин. Происхождение названий единиц измерения величин

1. Сравнение величин путем приложения предметов друг к другу.

2. Сравнение величин с помощью предмета-посредника (условной мерки).

3. Сравнение и измерение величин с помощью частей тела (локоть, ладонь).

4. Сравнение и измерение величин с помощью универсальных общепринятых условных мерок:

— чарка, штоф, бочка (для объемов),

— локоть, сажень, аршин (для расстояний),

— пуд, лот, фунт (для масс).

5. Введение метрической системы. Предложена в конце 18 в. учеными в Париже. Эта система мер принята не во всех странах. В СССР она использовалась с 1917 года. За основу измерения был принят метр (в пер. с греческого «измеряю»), величина которого равна приблизительно

1/40 000 000 части Гринвичского меридиана. Все остальные единицы измерения величин связаны с метром. Так 1 кг равен массе 1 дм 3 дистиллированной воды, 1 л равен объему этой же воды. Все остальные единицы измерения в 10 n раз больше или меньше основных (мм, дм, км, г, мг, мл и т.п.).

Свойства однородных величин:

1) для двух величин одного рода справедливо только одно из вы­сказываний: х=у или х у;

2) Отношение «быть большим по величине» ( х>у) является отно­шением порядка. Например, отношение «быть тяжелее» на множестве всех яблок является антирефлексивным (любое из яблок не тяжелее самого себя), антисимметричным (если яблоко х тяжелее яблока у, то яблоко у не тяжелее яблока х), транзитивным (если яблоко х тяжелее яблока у и яблоко у тяжелее яблока z, то яблоко х тяжелее яблока z);

3) отношение «быть одинаковым по величине» (х=у) является от­ношением эквивалентности. Например, «быть одинаковым по массе» на множестве всех яблок рефлексивно (каждое яблоко одинаково по массе с самим собой), симметрично (если яблоко х одинаково по массе с яблоком у, то яблоко у одинаково по массе с яблоком х), транзитивно (если яблоко х одинаково по массе с яблоком у и яблоко у одинаково по массе с яблоком z, то яблоко х одинаково по массе с яблоком z);

4) однородные величины можно складывать. Сложение величин обладает следующими свойствами:

а) переместительности, т.е. х+у=у+х,

б) сочетательности, т.е. x+(y+z)=(x+y)+z,

в) монотонности, т.е. х

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Основные положения однородных величин

Натуральное число как мера величины

Нам известно, что числа возникли из потребности счета и измерения. Если для счета предметов нам достаточно натуральных чисел, то для измерения нам необходимы действительные числа. В начальной школе в качестве результата измерения выступают натуральные числа. Мы также встанем на эту позицию, определив натуральное число как меру величины. Выясним, какой смысл имеют арифметические действия над натуральными числами с этой позиции.

Натуральные числа будем рассматривать в связи с измерением положительных скалярных величин: длин, площадей, масс, времени и др.

§1. Понятие положительной скалярной величины.

Рассмотрим два высказывания:

1.Многие окружающие нас объекты имеют длину;

2. Стол имеет длину.

Таким образом, термин «длина» применим для обозначения свойства целого класса объектов или одного объекта. Длина, это такое свойство объекта или объектов, которое проявляется в разной степени, т.е. можно сказать, что один стол длиннее другого, чего нельзя сказать о форме стола или о материале, из которого он сделан. Мы не можем сказать, что один стол «прямоугольнее» другого или «деревяннее»другого.

Таким образом, свойство «длина»- это особое свойство объектов, которое проявляется при сравнении их по протяженности. В процессе сравнения устанавливается, что два объекта либо имеют равные длины, либо длина одного больше длины другого объекта. Такие свойства объектов будем называть величинами.

Величины, выражающие одни и те же свойства объектов будем называть величинами одного рода или однородными величинами.

Основные положения однородных величин

1. Любые величины одного рода сравнимы: А=В либо А В.

2. Отношение «меньше» для однородных величин транзитивно: А А В.

5. Величину можно умножать на положительное действительное число, в результате получают величину того же рода х·А=В.

6. Величины одного рода можно делить, в результате получают число. Определение: Частным величин А и В называется такое положительное число х=А:В, что А=х∙В (деление определено через умножение величины на число).

Величины обладают одной особенностью, их можно оценить количественно. С этой целью величину надо измерить. Для измерения величины данного рода выбирают величину, называемую единицей измерения. Её будем обозначать Е.Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А – это значит найти такое положительное число х, что А=х·Е, х- численное значение величины А при выбранное единице величины Е или мера величины А при единице Е. Пишут х=m_Е(А).

Пример 1. А-длина отрезка а, Е- длина отрезка b, который в отрезке a укладывается 4 раза, тогда 4- мера длины отрезка а.

Пример 2. 2,6 кг=2,6∙кг, 13см=13·см, 16 с =16∙с.

Используя это представление, можно обосновать переход от одной единицы величины к другой.

ч= ·ч= ∙(60мин)= ( ∙60)мин=25мин.

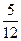
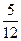
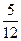
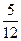
Определение.Величина, определяемая только численным значением, называется скалярной.

Определение.Величина, которая при выбранной единице измеренияопределяется положительным числом, называется положительной скалярной величиной.

Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к действиям над числами и наоборот.

1. Если величины А и В измерены с помощью единицы величины Е, то

2. Если величины А и В измерены с помощью единицы величины Е, то

Пример. А=5кг, В=3кг. =>А+В=5кг+3кг=(5+3)кг=8кг.

3. Если величины А и В таковы, что В=х∙А, а величина измерена с помощью единицы величины Е, то В=х∙А m(B)=х∙ m(A)

Пример. Еслимасса В в 3 раза больше массы А и А=2кг, то В=3 ∙А=3∙(2кг) =(3∙2)кг=6кг.

Рассмотренные понятия: объект (предмет, явление, процесс), его величина, её мера, единица величины- надо уметь вычленять в текстах и задачах.

Один и тот же объект может обладать несколькими величинами: для человека – рост (длина), масса, возраст (время), процесс равномерного движения связывает три величины S=V·t.

Аксиоматическое определение величины см. стр. 275.

Источник

Презентация по математике для начальных классов «Величины и их измерение»

Описание разработки

Приведите примеры различных величин, изучаемых в школе на уроках математики, физики. Вспомните единицы этих величин.

Разнородные величины выражают различные свойства объектов (один предмет может иметь массу, объем и др.).

Свойства однородных величин.

1. Однородные величины можно сравнивать. Для любых величин А и В справедливо только одно из отношений: А В, А=В.

Например, масса книги больше массы карандаша, а длина карандаша меньше длины стола.

2. Однородные величины можно складывать и вычитать. В результате получается величина того же рода. Величины, которые можно складывать, называются аддитивными.

Например, можно складывать длины предметов. В результате получается длина.

5. Величину можно оценить количественно, то есть измерить.

Измерение величин.

Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу.

Содержимое разработки

Величины и их измерение

Задание: Приведите примеры различных величин, изучаемых в школе на уроках математики, физики. Вспомните единицы этих величин.

Измерение величин Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. Цель измерения — получить численную характеристику данной величины при выбранной единице величины. Измерить величину А — это значит найти такое положительное действительное число х, что А=х*Е, где Е — величина того же рода, принятая за единицу. Число х называют численным значением величины А при единице величины Е. Численное значение величины показывает, во сколько раз заданная величина больше или меньше величины, принятой за единицу. Пример. 1) Если масса дыни 3 кг, то 3 — численное значение массы дыни при единице массы килограмм.

B – mn A3 » width=»640″

Значение измерения очень велико. Не всегда можно сравнить или сложить (вычесть) величины непосредственно (например, длину дорог). Измерение позволяет свести сравнение величин к сравнению чисел, а действия с величинами – к действиям над числами, что значительно проще. Взаимосвязь величин и их численных значений Если величины А и В измерены с помощью единицы величины Е, то отношения между величинами А к В будут такими же, как и отношения между их численными значениями (и наоборот):Пусть А=m*Е, В=n*Е, тогда: А=B – m=n AB – mn A3

Площадь фигуры Площадь — положительная величина, определенная на множестве плоских фигур так, что: равные фигуры имеют равные площади; если фигура составлена из конечного числа фигур, то ее площадь равна сумме их площадей. Некоторые свойства площадей : 1. Если фигуры равны, то равны численные значения их площадей (при одной и той же единице площади). Обратное – неверно. 2. Численное значение площади фигуры равно сумме численных значений площадей ее составляющих частей (при одной и той же единице площади) 3. При замене единицы площади численное значение площади увеличивается (уменьшается) во столько раз, во сколько раз новая единица меньше (больше) старой.

Промежутки времени Окружающий нас мир существует во времени. Временные характеристики явлений (продолжительность, последовательность, частота, ритм, темп и др.) необходимы для описания любых процессов в природе. Понятие времени более сложное, чем понятие длины, площади, массы. Оно не имеет наглядности и познается опосредованно. Вся жизнь человека связана со временем, с умением измерять, распределять, ценить время. Время течет непрерывно, его нельзя ни остановить, ни возвратить, ни увидеть, что создает особые трудности в изучении. Некоторые свойства промежутков времени 1. Промежутки времени можно сравнивать, («Красная Шапочка затратила больше времени на дорогу до бабушки, чем Серый Волк».) 2. Промежутки времени можно складывать и вычитать. («Маша один час вырезала фигуры и один час их наклеивала. Сколько всего времени она затратила на работу?») 3. Промежутки времени можно умножать на число. («7 суток — это неделя. Сколько суток в трех неделях?») 4. Промежутки времени можно измерять. В качестве единицы времени выбирается регулярно повторяющийся процесс. Такие единицы времени, как год, сутки, были выбраны на основе природных явлений: смены дня и ночи, смены времен года, а час, минута, секунда придуманы человеком.

Источник