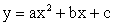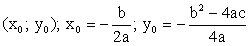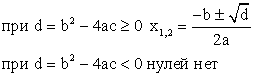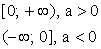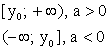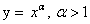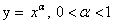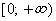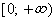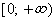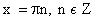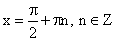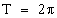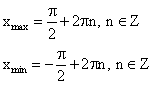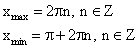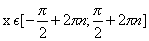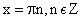Что значит область определения функции симметрична относительно нуля
Четные и нечетные функции
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
Глоссарий по теме урока
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Функция у = f(х) называется четной, если она обладает двумя свойствами:
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
для любого х из области определения выполняется равенство f(-х)=-f(х).
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1 у2.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
D(y)= 

следовательно, функция четная и ее график симметричен относительно оси ОУ
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
у>0 при
у 2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x 2 у.е.
Причем 0≤ x ≤ 24, x ϵ N.
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
область определения – множество действительных чисел – симметрична относительно нуля
Данная функция одновременно четна и нечетна.
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
логарифмируемое выражение должно быть положительным
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
и четная, и нечетная
2.
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Что значит область определения функции симметрична относительно нуля
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
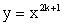
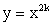
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
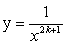
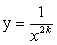
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме
R кроме
Параграф 2. Повторение и расширение сведений о функции.
Работу выполнил: Косярский А.А. студент группы 45.2
Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.
1. Понятие числовой функции
2. График функции
Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x
3. Возрастающие и убывающие функции
Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)
Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2)
4. Чётные и нечётные функции
Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy
Объяснение и обоснование
1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.
Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.
Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).
Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.
Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).
Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]
3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.
На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).
Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.
То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) x1 имеем
-2⋅
отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.
Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.
4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).
Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.
Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.
Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.
ВОПРОСЫ ДЛЯ КОНТРОЛЯ:
ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ
УПРАЖНЕНИЯ К ПАРАГРАФУ
5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x 5 5) y = √(x)
8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x 0
9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.
11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.
12. Обоснуйте, что заданная функция является чётной:
1) y = x 6 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x 4 )
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
Глоссарий по теме урока
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Функция у = f(х) называется четной, если она обладает двумя свойствами:
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
для любого х из области определения выполняется равенство f(-х)=-f(х).
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1 у2.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
D(y)= 

следовательно, функция четная и ее график симметричен относительно оси ОУ
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
у>0 при
у 2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x 2 у.е.
Причем 0≤ x ≤ 24, x ϵ N.
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
область определения – множество действительных чисел – симметрична относительно нуля
Данная функция одновременно четна и нечетна.
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
логарифмируемое выражение должно быть положительным
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
и четная, и нечетная
2.
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.