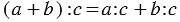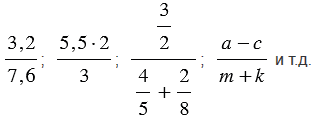Что значит найти частное в дроби
Математика. 6 класс
Конспект урока
Перечень рассматриваемых вопросов:
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей делимого и делителя.
Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы изучали правила умножения дробей.
Сегодня рассмотрим правила деления.
Аналогично умножению, дроби с любыми знаками делят по тем же правилам, что и положительные дроби.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Найдём частное от деления двух дробей.
Запишем равенство, которое можно получить на основании правила деления.
Чтобы разделить дробь на целое, не равное нулю число, можно её знаменатель умножить на это число.
Знак «–» перед дробью, можно записывать и в знаменателе, и в числители дроби, то есть верны равенства:
Используя свойство взаимно обратных дробей, что их произведение равно 1, можем сформулировать следующее утверждение:
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Правила знаков, при делении дробей
Правило деления дробей с одинаковыми знаками
Частным двух дробей с одинаковыми знаками является положительная дробь, равная частному модулей делимого и делителя.
Правило деления дробей с разными знаками
Частное от деления дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Из правил деления дробей с любыми знаками следует, что их можно делить по тем же правилам, что и целые числа. То есть мы можем сначала определять знак результата, а потом выполнять действия с модулями.
Найдём, сколько автомобиль проехал за второй час. Известно, что в 2 раза меньше, чем за первый, значит, путь за первый час разделим на 2.
Найдём общую часть пути за два часа.
Для этого сложим части пути за первый и за второй час.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
деление дробей с одинаковыми знаками
деление дробей с разными знаками
деление дроби на целое число
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
№ 2. Вставьте в текст нужные слова.
Частное двух дробей есть дробь, … которой равен … числителя первой дроби и … второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Варианты слов для вставки:
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
§ Смешанные числа. Целая часть дроби. Правильные и неправильные дроби
Основное свойство дроби
Возникает резонный вопрос: как найти все дроби, равные данной? Ответ дадим в форме определения:
— числитель и знаменатель можно умножать на одно и то же число, отличное от нуля. При этом получится дробь, равная данной.
Это очень важное свойство — запомните его. С помощью основного свойства дроби можно упрощать и сокращать многие выражения. В будущем оно постоянно будет «всплывать» в виде различных свойств и теорем.
Видео
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения 
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ 

Выражение 

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится 
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения 
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на 
Чтобы разделить число 1 на 


Выражение 
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Алгоритм превращения
Переводить неправильную дробь в правильную или выполнять обратную операцию просто, если следовать алгоритму. Так как сделать это напрямую нельзя, то фактически получится преобразование в запись, содержащую целую и дробную часть.
Превратить неправильное выражение в смешанное можно по следующему алгоритму:
Это упрощённый способ, быстро позволяющий выполнить перевод числа из одной формы в другую. Математическое равенство, описывающее это правило, будет выглядеть так: n a/b = ((n * b) + a)/b.
Чтобы преобразовать дробь по всем правилам, нужно сделать следующее. Так как смешанное отношение, по сути, является суммой целого и части, понадобится просто выполнить сложение. Для этого первое слагаемое представляют как неправильную дробь. Сделать это можно, разделив целое на единицу. Затем действуют по правилу сложения дробей, то есть находят общий знаменатель, дополнительные множители, выполняют складывание в числителе: n a/b = n/1 + a/b = ((n *b) + a)/b.
Из неправильной формы записи получить обычную дробь можно также через смешанную. Другими словами, представить выражение как сумму натурального числа и правильного отношения. Для этого необходимо выполнить 3 шага:
На самом деле выполнять деление числителя на знаменатель часто довольно сложно, поэтому поступают следующим образом. Делимое представляют в виде суммы дробей, но таким образом, чтобы деление одной из них можно было выполнить без остатка, то есть, m / n = (k + c) / n = k / n + c / n. Где целое число k / n, а c / n правильная дробь.
Нужно отметить, что некоторые выражения можно превращать в другую форму, не записывая поочерёдно действия, а выполняя все преобразования в уме. Но на начальном этапе рекомендуется весь процесс расписывать пошагово, пока не будет получен необходимый опыт. А только уже после переходить к переводу в уме.
Популярное
Навыки 15 декабря 2019
Математика 26 августа 2019 Найди закономерность Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
Любовь к учебе 6 сентября 2019 Как решать ребусы? Разгадывание ребусов – отличное времяпровождение для любителей всевозможных головоломок и загадок. Это захватывающий процесс, суть которого заключается в том, чтобы расшифровать слово, фразу или предложение с помощью картинок и символов-подсказок: цифр, букв, запятых и прочих знаков.
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
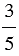
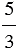
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 = 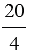
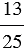
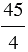
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
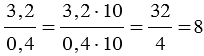
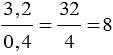
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
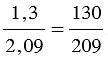
Поделись с друзьями в социальных сетях: