Что значит натурная модель
Большая Энциклопедия Нефти и Газа
Натурная модель
Натурные модели представляют наиболее объемную группу моделей, включающую как объекты естественного происхождения, так и объекты, полученные в результате деятельности человека. [1]
Реализация необходимой натурной модели осуществляется заданием определенных начальных и граничных условий на границах образца. Отражающую границу ( ЭС / Эх 0) реализуют в виде контакта образца с материалом диффузионной колонки ( ячейки), в котором скорость диффузии пренебрежимо мала по сравнению с диффузией в образце. Условие связывания обеспечивается поддержанием нулевой концентрации диффузанта на границе. Это достигается путем обеспечения на данной границе контакта образца с емкостью, объем которой на порядок больше объема образца или путем смывания образца по границе раствором с нулевой концентрацией диффузанта. Аналогично обеспечивается на границе другая заданная концентрация диффузанта. [2]
Стендовые испытания опытного образца машины, ее натурной модели или серийных образцов являются завершающим этапом проектирования и изготовления машин. Под стендовыми испытаниями понимаются испытания объекта, проводимые стационарно с применением испытуемого оборудования. В результате испытаний должны быть оценены фактические характеристики качества и надежности машины и установлено их соответствие техническим условиям. [6]
Предметом особого рассмотрения в учебных работах по пространственно-графическому моделированию является синтактический анализ изображения без какой-либо связи с натурной моделью или конкретным функционально-конструктивным содержанием. Дидактическая цель данного этапа обучения в согласии с принципом системного подхода заключается в предварительном изучении языка пространственно-графического моделирования. Студентам дается ориентировка в законах образования формальных графических структур, средствах выражения и возможностях в достижении различных целей. Оказалось, что такая ориентация в вопросах син-тактики формообразования, определяющих возможности графического моделирования, совершенно необходима для творческого овладения рассматриваемым предметом. [12]
Натурные и информационные модели
Вы будете перенаправлены на Автор24
Интуитивное и абстрактное восприятие
Способы восприятия внешнего мира человеком можно разделить на:
Интуиция — способность человека понимать смысл событий, ситуаций, объектов посредством подсознательного вывода, основанного на предшествующем опыте, воображении. Иными словами, это проницательность, «чутьё».
Рисунок 1. Дегустаторы вина за работой. Автор24 — интернет-биржа студенческих работ
При интуитивном постижении мира основанием для мыслительной деятельности являются ощущения, рефлексы, эмоции. Этот способ высшей нервной деятельности роднит человека с животными, которые больше доверяют своим ощущениям, чем логическим умозаключениям, хотя и логическая деятельность некоторым животным не чужда. Интуитивные модели познания, несмотря на присущую им субъективность, эффективны при экспертных оценках, т.е. оценках, основанных на опыте. Они важны, например, в работе дегустаторов. Интуитивное постижение мира свойственно деятелям культуры музыкантам, писателям, художникам и др.
Абстрактное мышление, напротив, позволяет в мыслительной деятельности отвлечься от субъективных (присущих конкретному индивиду) переживаний и выделить в наблюдаемом мире полезные закономерности. При этом часть информации, полученная в виде ощущений, теряется, зато появляется возможность описывать видение мира с помощью знаковых систем.
Готовые работы на аналогичную тему
В связи с вышесказанным, модели, помогающие понять окружающий мир, можно классифицировать как:
Рассмотрим их последовательно.
Натурные модели
Натурные модели применяют там, где для описания оценки окружающей обстановки важна полнота ощущений. Их удобно использовать там, где важно ориентироваться на какой-либо образец. Например, среди доказательств теоремы Пифагора есть варианты, где используются не формулы, а переливающаяся между сосудами соответствующих объемов жидкость.
Рисунок 2. Физическое доказательство теоремы Пифагора. Автор24 — интернет-биржа студенческих работ
В качестве примеров натурных моделей можно назвать игрушки, манекены, макеты, фотографии и т.д. Натурные модели-тренажеры применяют при подготовке летчиков, водителей и т.д. На них отрабатываются методы решения профессиональных проблем. Это позволяет избежать излишних материальных затрат, связанных с порчей дорогостоящего оборудования, поскольку тренажеры всегда дешевле, чем реальные устройства (самолеты, поезда, танки и т.п.).
Различают также модели-эрзацы, такие, как протезы, выполняющие функции настоящих органов или экзоскелеты, усиливающие возможности человеческого организма.
Свойством аналоговых (натурных) моделей является непрерывность: в них трудно выделить четко описываемые составные части. Примерами непрерывных моделей можно считать математические функции и графики.
Информационные модели
Как уже отмечено, при абстрагировании человеческое мышление способно формировать символьное, знаковое описание действительности. Потери информации при этом таковы, что их можно считать несущественными для практической деятельности. Например, покупатель, приобретая литровую упаковку молока, не задумывается о деталях производства и доставки этого продукта (абстрагируется от них), хотя товаровед и дегустатор могут сообщить об этом товаре много дополнительных экспертных данных, проанализировав внешний вид, вкус и запах.
Таким образом, информационные модели, в отличие от натурных, всегда предполагают детализацию полученных ощущений в ущерб достоверности. Без этого невозможно формирование символьных (знаковых) систем.
Рисунок 3. Нотная запись как музыкальный алфавит. Автор24 — интернет-биржа студенческих работ
Знаковые информационные модели называют также дискретными, поскольку информация в них представлена в посредством набора раздельных символов (алфавита) и формируемого на их основе языка. При этом языки делятся на:
Формализованные языки имеют фиксированный набор лексических единиц и строгий синтаксис фраз. Этим обеспечивается однозначность трактовки и исполнения сформулированных указаний. Примерами моделей, создаваемых посредством формализованных языков, служат математические описания, записи шахматных партий, нотная запись музыки.
Формализованные языки позволяют реализовывать информационные модели в виде компьютерных программ и двоичных данных, поскольку любой конечный алфавит можно преобразовать в цифровую, и, в конечном итоге, в двоичную форму записи.
Модель
Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве (процессе, …) свойств и закономерностей. Применяют для нужд познания (созерцания, анализа и синтеза).
Моделирование является обязательной частью исследований и разработок, неотъемлемой частью нашей жизни, поскольку сложность любого материального объекта и окружающего его мира бесконечна вследствие неисчерпаемости материи и форм её взаимодействия внутри себя и с внешней средой.
Одни и те же устройства, процессы, явления и т. д. (далее — «системы») могут иметь много разных видов моделей. Как следствие, существует много названий моделей, большинство из которых отражает решение некоторой конкретной задачи. Ниже приведена классификация и дана характеристика наиболее общих видов моделей.
Содержание
Требования к моделям
Моделирование всегда предполагает принятие допущений той или иной степени важности. При этом должны удовлетворяться следующие требования к моделям:
Выбор модели и обеспечение точности моделирования считается одной из самых важных задач моделирования.
Точность моделей
Погрешности моделирования вызываются как объективными причинами, связанными с упрощением реальных систем, так и субъективными, обусловленными недостатком знаний и навыков, особенностями характера того или иного человека. Погрешности можно предотвратить, компенсировать или учесть. И всегда обязательна оценка правильности получаемых результатов. В технике быструю оценку точности модели часто проводят следующими способами:
Известно, что посредством грубых измерений, использования контрольно-измерительных приборов с низкой точностью или приближенных исходных данных невозможно получить точные результаты. С другой стороны, бессмысленно вести, например, расчет с точностью до грамма, если результат потом нужно округлять (скажем, указывать в формуляре) с точностью до ста грамм, или же определять среднюю величину точнее составляющих её значений, и т. д. Поэтому важно помнить о следующем:
Основные виды моделей
По способу отображения действительности различают три основных вида моделей — эвристические, натурные и математические.
Эвристические модели
Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальная информационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений.
Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.
Натурные модели
Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:
Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчетов. Физическая модель позволяет охватить явление или процесс во всём их многообразии, наиболее адекватна и точна, но достаточно дорога, трудоемка и менее универсальна. В том или ином виде с физическими моделями работают на всех этапах проектирования;
Математические модели
Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:
Построение математических моделей возможно следующими способами (более подробно — см. Математическая модель):
Математические модели более универсальны и дешевы, позволяют поставить «чистый» эксперимент (то есть в пределах точности модели исследовать влияние какого-то отдельного параметра при постоянстве других), прогнозировать развитие явления или процесса, отыскать способы управления ими. Математические модели — основа построения компьютерных моделей и применения вычислительной техники.
Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования — с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула — это разновидность модели и, следовательно, не является абсолютной истиной, а всего лишь этап на пути её познания.
Промежуточные виды моделей
К промежуточным видам моделей можно отнести:
Существует и другие виды «пограничных» моделей, например, экономико-математическая и т. д.
Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом устройстве и возможностей инженера, исследователя. По возрастанию степени соответствия реальности модели можно расположить в следующий ряд: эвристические (образные) — математические — натурные (экспериментальные).
Уровни моделей
Количество параметров, характеризующих поведение не только реальной системы, но и её модели, очень велико. Для упрощения процесса изучения реальных систем выделяют четыре уровня их моделей, различающиеся количеством и степенью важности учитываемых свойств и параметров. Это — функциональная, принципиальная, структурная и параметрическая модели.
Функциональная модель
Функциональная модель предназначена для изучения особенностей работы (функционирования) системы и её назначения во взаимосвязи с внутренними и внешними элементами.
Функция — самая существенная характеристика любой системы, отражает её предназначение, то, ради чего она была создана. Подобные модели оперируют, прежде всего, с функциональными параметрами. Графическим представлением этих моделей служат блок-схемы. Они отображают порядок действий, направленных на достижение заданных целей (т. н. ‘функциональная схема’). Функциональной моделью является абстрактная модель.
Модель принципа действия
Модель принципа действия (принципиальная модель, концептуальная модель) характеризует самые существенные (принципиальные) связи и свойства реальной системы. Это — основополагающие физические, биологические, химические, социальные и т. п. явления, обеспечивающие функционирование системы, или любые другие принципиальные положения, на которых базируется планируемая деятельность или исследуемый процесс. Стремятся к тому, чтобы количество учитываемых свойств и характеризующих их параметров было небольшим (оставляют наиболее важные), а обозримость модели — максимальной, так чтобы трудоемкость работы с моделью не отвлекала внимание от сущности исследуемых явлений. Как правило, описывающие подобные модели параметры — функциональные, а также физические характеристики процессов и явлений. Принципиальные исходные положения (методы, способы, направления и т. д.) лежат в основе любой деятельности или работы.
Так, принцип действия технической системы — это последовательность выполнения определенных действий, базирующихся на определенных физических явлениях (эффектах), которые обеспечивают требуемое функционирование этой системы. Примеры моделей принципа действия: фундаментальные и прикладные науки (например, принцип построения модели, исходные принципы решения задачи), общественная жизнь (например, принципы отбора кандидатов, оказания помощи), экономика (например, принципы налогообложения, исчисления прибыли), культура (например, художественные принципы).
Работа с моделями принципа действия позволяет определить перспективные направления разработки (например, механика или электротехника) и требования к возможным материалам (твердые или жидкие, металлические или неметаллические, магнитные или немагнитные и т. д.).
Правильный выбор принципиальных основ функционирования предопределяет жизнеспособность и эффективность разрабатываемого решения. Так, сколько бы ни совершенствовали конструкцию самолета с винтомоторным двигателем, он никогда не разовьет сверхзвуковую скорость, не говоря уже о полетах на больших высотах. Только использование другого физического принципа, например, реактивного движения и созданного на его основе реактивного двигателя, позволит преодолеть звуковой барьер.
Например, для технических моделей эти схемы отражают процесс преобразования вещества, как материальной основы устройства, посредством определенных энергетических воздействий с целью реализации потребных функций (функционально-физическая схема). На схеме виды и направления воздействия, например, изображаются стрелками, а объекты воздействия — прямоугольниками.
Структурная модель
Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать:
Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса.
Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей).
Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Её примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам.
Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x1, х2, …) = 0, неравенств f (x1, х2, …) > 0 и в иных выражениях.
Параметрическая модель
Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы. Графической интерпретацией такой модели в технике служит чертеж устройства или его частей с указанием численных значений параметров.
Классификация моделей
По целям исследований
В зависимости от целей исследования выделяют следующие модели:
По особенностям представления
С целью подчеркнуть отличительную особенность модели их подразделяют на простые и сложные, однородные и неоднородные, открытые и закрытые, статические и динамические, вероятностные и детерминированные и т. д. Стоит отметить, что когда говорят, например, о техническом устройстве как простом или сложном, закрытом или открытом и т. п., в действительности подразумевают не само устройство, а возможный вид его модели, таким образом подчеркивая особенность состава или условий работы.
Знание этих особенностей облегчает процесс моделирования, так как позволяет выбрать вид модели, наилучшим образом соответствующей заданным условиям. Этот выбор основывается на выделении в системе существенных и отбрасывании второстепенных факторов и должен подтверждаться исследованиями или предшествующим опытом. Наиболее часто в процессе моделирования ориентируются на создание простой модели, что позволяет сэкономить время и средства на её разработку. Однако повышение точности модели, как правило, связано с ростом её сложности, так как необходимо учитывать большое число факторов и связей. Разумное сочетание простоты и потребной точности и указывает на предпочтительный вид модели.
Урок 11
Понятие модели.
Назначение и свойства моделей.
Графические информационные модели
Содержание урока
Что такое моделирование. Натурные и информационные модели
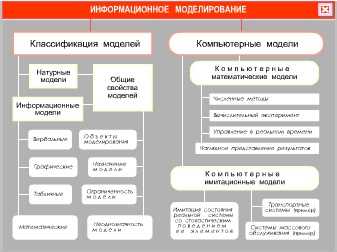
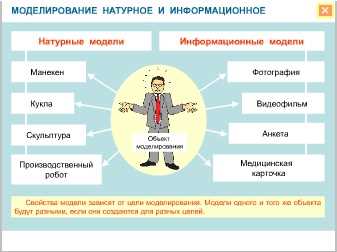
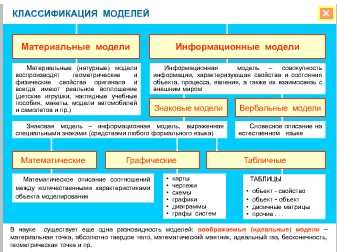
Любая модель воспроизводит только те свойства оригинала, которые понадобятся человеку при ее использовании. Например, манекен и производственного робота можно назвать моделями человека. Манекен нужен для того, чтобы на него можно было надеть одежду для рекламы или для удобства работы портного, но способности ходить, мыслить или разговаривать от него не требуется. Поэтому манекен должен воспроизводить лишь форму и размер человеческого тела.
Свойства объекта, отраженные в модели, зависят от цели моделирования. Модели одного и того же объекта будут разными, если они создаются для разных целей.
Что такое моделирование. Формализация