Что значит формальные языки
Формальные языки и грамматики
Математический язык как форма выражения научного знания использовался еще в древности при решении практических задач.
Большую роль в развитии математики как языка – метаязыка наук – сыграла математическая логика, аксиоматизировавшая ряд теории, изучившая их логику, внутреннюю структуру.
Язык как коммуникативный аппарат должен иметь определяющие конструкции слов над данным алфавитом, грамматические правила образования предложений из слов и соотнесения этих предложений тем явлениям и процессам, которые они описывают, или синтаксическим и семантическим правилам.
Пример. В частности, семантика изучает связи вида:
«знак, структура знаков 

синтаксис – связи вида:
«знак, структура знаков 
Пример. Запишем более кратко, сжато, точно (формализованно) факт » целое число x делится на целое число y без остатка». На математическом языке это будет иметь вид «Число x кратно числу y «. Факт, что числа x, y – целые, уже можно специально, как выше, не оговаривать, так как математическое понятие кратности это уже предполагает ( аксиома ). Запишем еще более кратко и формализованно на алгоритмическом языке Паскаль : » x mod y = 0 «. Здесь уже условие кратности область изменения аргументов не нужно оговаривать – они декларированы в языке Паскаль (в описаниях типов и операции mod ).
Языки бывают естественного происхождения (например языки общения) и искусственного происхождения или формальные языки, разрабатываемые для общения человека с автоматом (компьютером) либо для описания и получения знаний.
Язык (множество слов S(X) ) задается грамматикой G(S) – структурой правил, которые позволяют порождать все слова 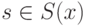
Грамматический анализ – процесс редукции к нетерминальному символу или слову.
Формальные и естественные языки
Естественные языки являются языками, на которых говорят люди, такие как английский, испанский, и французский языки. Они не были разработаны людьми (хотя люди пытаются навязать какие-то правила для них); они развивались естественным путем.
Формальные языки являются языками, которые разработаны людьми для конкретных применений. Например, нотация, которую математики используют как формальный язык, которая особенно хороша для обозначения отношений между числами и символами. Химики используют формальный язык для представления химической структуры молекул. И самое важное:
Языки программирования являются формальными языками, которые были разработаны для расчетных выражений.
Формальные языки, как правило, имеют строгие правила синтаксиса. Например, 3+3=6 является синтаксически правильным математическим утверждением, но 3=+$6 — нет. H2O является синтаксически правильным химическим названием, но 2ZZ — нет.
В качестве упражнения создайте то, что выглядит хорошо структурированным английским предложением с неузнаваемыми лексемами в нем. Затем напишите еще одно предложение со всеми действующими лексемами, но с недопустимой структурой.
Когда вы читаете предложение на английском языке или оператор на формальном языке, вы должны выяснить, какова структура предложения присутствует (хотя на естественном языке вы делаете это подсознательно). Этот процесс называется синтаксическим анализом.
Например, когда вы слышите фразу «Второй ботинок упал», вы понимаете, что «второй ботинок» является предметом, а «упал» — предикатом. После того как вы разобрали предложение, вы можете выяснить его значение либо его семантику. Предполагая, что вы знаете, что такое «ботинок» и что это значит падать, вы будете понимать общий подтекст этого предложения.
Хотя у формальных и естественных языков есть много особенностей в общих лексемах, структуре, синтаксисе и семантике, там много различий:
неоднозначность — естественные языки полны двусмысленности, когда люди общаются с помощью контекстных подсказок и другой информации. Формальные языки разработаны быть почти или полностью однозначными, что означает, что любое утверждение имеет ровно одно значение, вне зависимости от контекста.
избыточность — Для компенсации двусмысленности и уменьшения недопонимания естественные языки используют много избыточности. В результате они часто многословны. Формальные языки являются менее избыточными и более краткими.
буквальность — естественные языки полны идиом и метафор. Если я говорю: «Второй ботинок упал» там, вероятно, нет никакой обуви и нечему падать. Формальные языки означают именно то, что они говорят.
Людям, которые растут, разговаривая на естественном языке, часто приходится приспосабливаться к формальным языкам. В некотором смысле разница между формальным и естественным языками подобна разнице между поэзией и прозой, но в большей степени:
— слова используются для их впечатления, а также для их смысла, и все стихотворение вместе создает эффект или эмоциональный отклик. Неоднозначность не только общепринята, но часто является преднамеренной.
— буквальное значение слова является более важным, а структура способствует большему пониманию. Проза более поддается анализу, чем поэзия, но до сих пор часто неоднозначна.
— значение компьютерной программы однозначно и буквально, и может быть осознано полностью посредством анализа лексем и структуры.
Вот несколько советов для чтения программ (и других формальных языков). Во-первых, помните, что формальные языки являются гораздо более плотными, чем естественные языки, так что понадобится больше времени, чтобы прочитать их. Кроме того, структура очень важна, так что поэтому не очень хорошая идея читать сверху вниз, слева направо. Вместо этого, научитесь анализировать программу в вашей голове, идентифицируя лексемы и интерпретируя структуру. В довершение ко всему, детали имеют значение. Мелочи, такие как орфографические ошибки и плохая пунктуация, которые могут вам сойти с рук в естественных языках, могут иметь большое значение в формальном языке.
Традиционно первая программа, которую пишут на новом языке, называется «Hello, World!», потому что всё, что она делает — это отображает слова «Hello, World!». В Python, это выглядит следующим образом:
Это пример оператора печати, который на самом деле не печатает ничего на бумаге. Он отображает значение на экране. В этом случае результатом являются слова:
Кавычки в программе отмечают начало и конец значения; они не появляются в результате.
Некоторые люди судят о качестве языка программирования по простоте программы «Hello, World!». По этому образцу, Python делает это настолько, насколько это возможно.
Решение проблемы — процесс разработки проблемы, нахождение решения и отражение решения.
Язык программирования высокого уровня — язык программирования, подобный Python, который задуман быть легким для людей, чтобы читать и писать.
Низкоуровневый язык — язык программирования, который разработан, чтобы быть естественным для выполнения компьютером; также называемый «машинным языком» или «языком ассемблера».
Переносимость — свойство программы, которая может работать на более чем одном виде компьютеров. интерпретация — выполнение программы на языке высокого уровня с помощью перевода одной его строки за один раз.
Компиляция — одноразовый перевод программы, написанной на языке высокого уровня, на язык низкого уровня в рамках подготовки для последующего выполнения.
Исходный код — программа на языке высокого уровня перед ее компиляцией. объектный код — вывод компилятора после того, как он перевел программу. выполняемый код — другое имя для «объектного кода», который готов к выполнению. сценарий — программа, хранимая в файле (как правило та, которая будет интерпретироваться).
Программа — набор инструкций, который определяет вычисления. алгоритм — общий процесс решения класса проблем.
Баг — ошибка в программе. отладка — процесс поиска и удаления любой из трех типов ошибок программирования.
Синтаксис — структуры программы. синтаксическая ошибка — ошибка в программе, которая делает невозможным анализ (и, следовательно, невозможность интерпретации).
Ошибка выполнения — ошибка, которая не встречается, пока программа не начнет выполняться, но которая предотвращает продолжение программы.
Исключение — другое название ошибки выполнения. семантическая ошибка — ошибка в программе, которая заставляет ее делать что-то другое, чем то, что подразумевалось программистом.
Семантика — смысл программы. естественный язык — любой из языков, на котором говорят люди и которые развивались естественным образом.
Формальный язык — любой из языков, который люди разработали для определенных целей, таких как представление математических идей или компьютерных программ; все языки программирования являются формальными языками.
Лексема — один из основных элементов синтаксической структуры программы, аналогичный слову на естественном языке.
Синтаксический анализ — изучение программы и анализ синтаксической структуры.
Оператор печати — инструкция, которая вызывает интерпретатор Python для отображения значения на экране.
Статьи к прочтению:
Естественные и формальные язык. Формы представления информации | Информатика 7 класс #8 | Инфоурок
Похожие статьи:
Если речь идёт о составлении алгоритмов для процессора ЭВМ (электронно-вычислительной машины), исполнителем является процессор. Упрощённая модель…
Иску?сственные языки? — специальные языки, которые, в отличие от естественных, сконструированы целенаправленно. Таких языков существует уже более тысячи,…
Формальный язык: характеристики и примеры
Содержание:
В формальный язык это набор лингвистических знаков для исключительного использования в ситуациях, когда естественный язык не подходит. В целом язык делится на естественный или неформальный и искусственный. Первый используется в обычных ситуациях повседневной жизни. Между тем, искусственное используется в конкретных ситуациях, выходящих за рамки повседневной жизни.
Таким образом, формальный язык входит в группу искусственных. Это используется, в частности, в формальных науках (тех, чья сфера действия не является реальностью физического мира, а абстрактного мира). Некоторые из этих наук включают логику, математику и компьютерное программирование.
Теперь этот тип языка использует набор символов или букв в качестве алфавита. Отсюда образуются «языковые цепочки» (слова). Они, если они соответствуют правилам, считаются «правильно построенными словами» или «правильно построенными формулами».
характеристики
Ограниченная среда
Формальный язык предназначен для обмена данными в условиях окружающей среды, отличных от условий других языков. Например, в языке программирования целью является общение между людьми и компьютерами или между компьютерными устройствами. Это не общение между людьми.
Так что это язык для этого случая, созданный с определенной целью и функционирующий в очень специфических условиях. Кроме того, он не получил широкого распространения. Напротив, его использование ограничено теми, кто знает как цель языка, так и его конкретный контекст.
Грамматические правила априори
Формальный язык формируется из установления априорных грамматических правил, которые дают ему основу. Таким образом, сначала разрабатывается набор принципов, которые будут определять комбинацию элементов (синтаксис), а затем генерируются формулы.
С другой стороны, развитие формального языка носит сознательный характер. Это означает, что для их обучения требуются постоянные усилия. В том же порядке идей его использование ведет к специализации в правилах и условностях научного использования.
Минимальная семантическая составляющая
Семантическая составляющая в формальном языке минимальна. Данная строка, принадлежащая формальному языку, сама по себе не имеет значения.
Семантическая нагрузка, которую они могут иметь, частично исходит от операторов и отношений. Вот некоторые из них: равенство, неравенство, логические связки и арифметические операторы.
В естественном языке повторение комбинации «p» и «a» в слове «папа» имеет семантическое значение parent. Однако на формальном языке это не так. В практической области значение или интерпретация цепей основывается на теории, которую человек пытается определить с помощью этого формального языка.
Таким образом, когда он используется для линейных систем уравнений, он имеет теорию матриц как одно из своих семантических значений. С другой стороны, эта же система несет семантическую нагрузку логических схем в вычислениях.
В заключение, значение этих цепочек зависит от области формальных наук, в которой они применяются.
Символический язык
Форма построения символов формального языка позволяет производить вычисления и устанавливать истины в зависимости не от фактов, а от их взаимосвязи. Этот символизм уникален и далек от любой конкретной ситуации в материальном мире.
Универсальность
Формальный язык носит универсальный характер. В отличие от естественного, который, мотивированный своей субъективностью, допускает толкования и множественные диалекты, формальный остается неизменным.
На самом деле это похоже для разных типов сообществ. Его утверждения имеют одинаковое значение для всех ученых, независимо от того, на каком языке они говорят.
Точность и выразительность
В целом формальный язык точен и не очень выразителен. Правила его формирования не позволяют говорящим придумывать новые термины или придавать новое значение существующим терминам. И его нельзя использовать для передачи убеждений, настроений и психологических ситуаций.
Возможность расширения
По мере того как был достигнут прогресс в открытии приложений для формального языка, его развитие было экспоненциальным. Тот факт, что им можно управлять механически, не задумываясь о его содержании (его значениях), позволяет свободно комбинировать его символы и операторы.
Теоретически возможности расширения безграничны. Например, недавние исследования в области вычислений и информатики связывают оба языка (естественный и формальный) в практических целях.
В частности, группы ученых работают над способами улучшения эквивалентности между ними. В конце концов, стремятся создать интеллект, который может использовать формальный язык для создания естественного языка.
Примеры
Логика
В строке: (p⋀q) ⋁ (r⋀t) => t буквы p, q, r, t символизируют предложения без какого-либо конкретного значения. С другой стороны, символы ⋀, ⋁ и => представляют соединительные элементы, связывающие предложения. В этом конкретном примере используются соединители «и» (⋀), «или» (⋁), «затем» (=>).
Ближайший перевод к строке: если какое-либо из выражений в скобках истинно или неверно, тогда t истинно или нет. Соединители отвечают за установление отношений между предложениями, которые могут представлять что угодно.
Математика
В этом математическом примере A = ❴x | x⦤3⋀x> 2❵ вмешивается набор с именем «A», который имеет элементы с именем «x». Все элементы A связаны символикой ❴, |, ⦤, ⋀,>, ❵.
Все они используются здесь для определения условий, которым должны удовлетворять элементы «x», чтобы они были из множества «A».
Объяснение этой цепочки состоит в том, что все элементы этого набора соответствуют условию быть меньше или равным 3 и в то же время больше 2. Другими словами, эта цепочка определяет число 3, которое является единственным элементом, который соответствует условиям.
Компьютерное программирование
Строка программирования IF A = 0, THEN GOTO 30, 5 * A + 1 имеет переменную «A», которая подвергается проверке и процессу принятия решения с помощью оператора, известного как «if conditional».
Выражения «IF», «THEN» и «GOTO» являются частью синтаксиса оператора. Между тем, остальные элементы являются значениями сравнения и действия «А».
Его значение таково: компьютеру предлагается оценить текущее значение «А». Если он равен нулю, он перейдет к «30» (другая строка программирования, где будет другая инструкция). Если он отличен от нуля, тогда переменная «A» будет умножена ( *) на значение 5, и к ней будет добавлено значение 1 (+).
Ссылки
10 лучших гериатрических резиденций в Мурсии
Формальный язык
В математической логике и информатике формальный язык — это множество конечных слов (строк, цепочек) над конечным алфавитом. Понятие языка чаще всего используется в теории автоматов, теории вычислимости и теории алгоритмов. Научная теория, которая имеет дело с этим объектом, называется теорией формальных языков.
В теории моделей язык соответствует не языку в информатике, а скорее алфавиту. Язык состоит из множеств символов, функций и отношений вместе с их арностью, а также множество переменных. Каждое из этих множеств может быть бесконечным. Из языка вместе с универсальными логическими символами составляются логические высказывания.
Определение
Формальный язык может быть определён по-разному, например:
Если алфавит задан как <a, b>, а язык L включает в себя все слова над ним, то слово ababba принадлежит L. Пустое слово (то есть строка нулевой длины) допускается и часто обозначается как e, ε или Λ.
Некоторые примеры формальных языков:
Операции
Некоторые операции могут быть использованы для того, чтобы порождать новые языки из данных. Предположим, что 

Формальные языки и грамматики
Мотивация
Время от времени на Хабре публикуются посты и переводные статьи, посвященные тем или иным аспектам теории формальных языков. Среди таких публикаций (не хочется указывать конкретные работы, чтобы не обижать их авторов), особенно среди тех, которые посвящены описанию различных программных инструментов обработки языков, часто встречаются неточности и путаница. Автор склонен считать, что одной из основных причин, приведших к такому прискорбному положению вещей, является недостаточный уровень понимания идей, лежащих в основании теории формальных языков.
Этот текст задуман как популярное введение в теорию формальных языков и грамматик. Эта теория считается (и, надо сказать, справедливо) довольно сложной и запутанной. На лекциях студенты обычно скучают и экзамены тем более не вызывают энтузиазма. Поэтому и в науке не так много исследователей в этой тематике. Достаточно сказать, что за все время, с зарождения теории формальных грамматик в середине 50-х годов прошлого века и до наших дней, по этому научному направлению было выпущено всего две докторских диссертации. Одна из них была написана в конце 60-х годов Алексеем Владимировичем Гладким, вторая уже на пороге нового тысячелетия — Мати Пентусом.
Далее в наиболее доступной форме описаны два основных понятия теории формальных языков: формальный язык и формальная грамматика. Если тест будет интересен аудитории, то автор дает торжественное обещание разродиться еще парой подобных опусов.
Формальные языки
Коротко говоря, формальный язык — это математическая модель реального языка. Под реальным языком здесь понимается некий способ коммуникации (общения) субъектов друг с другом. Для общения субъекты используют конечный набор знаков (символов), которые проговариваются (выписываются) в строгом временном порядке, т.е. образуют линейные последовательности. Такие последовательности обычно называют словами или предложениями. Таким образом, здесь рассматривается только т.н. коммуникативная функция языка, которая изучается с использованием математических методов. Другие функции языка здесь не изучаются и, потому, не рассматриваются.
В качестве известного примера такой математической абстракции можно привести модель, известную под неблагозвучным для русского уха названием «мешок слов». В этой модели исследуются тексты естественного языка (т.е. одного из тех языков, которые люди используют в процессе повседневного общения между собой). Основной объект модели мешка слов — это слово, снабженное единственным атрибутом, частотой встречаемости этого слова в исходном тексте. В модели не учитывается, как слова располагаются рядом друг с другом, только сколько раз каждое слово встречается в тексте. Мешок слов используется в машинном обучении на основе текстов в качестве одного из основных объектов изучения.
Но в теории формальных языков представляется важным изучить законы расположения слов рядом друг с другом, т.е. синтаксические свойства текстов. Для этого модель мешка слов выглядит бедной. Поэтому формальный язык задается как множество последовательностей, составленных из элементов конечного алфавита. Определим это более строго.
Алфавит представляет собой конечное непустое множество элементов. Эти элементы будем называть символам. Для обозначения алфавита обычно будем использовать латинское V, а для обозначения символов алфавита — начальные строчные буквы латинского алфавита. Например, выражение V =
Цепочка представляет собой конечную последовательность символов. Например, abc — цепочка из трех символов. Часто при обозначении цепочек в символах используют индексы. Сами цепочки обозначают строчными символами конца греческого алфавита. Например, omega = a1. an — цепочка из n символов. Цепочка может быть пустой, т.е. не содержать ни одного символа. Такие цепочки будем обозначать греческой буквой эпсилон.
Наконец, формальный язык L над алфавитом V — это произвольное множеств цепочек, составленных из символов алфавита V. Произвольность здесь означает тот факт, что язык может быть пустым, т.е. не иметь ни одной цепочки, так и бесконечным, т.е. составленным из бесконечного числа цепочек. Последний факт часто вызывает недоумение: разве имеются реальные языки, которые содержат бесконечное число цепочек? Вообще говоря, в природе все конечно. Но мы здесь используем бесконечность как возможность образования цепочек неограниченной длины. Например, язык, который состоит из возможных имен переменных языка программирования C++, является бесконечным. Ведь имена переменных в C++ не ограничены по длине, поэтому потенциально таких имен может быть бесконечно много. В реальности, конечно, длинные имена переменных не имеют для нас особого смысла т.к. к концу чтения такого имени уже забываешь его начало. Но в качестве потенциальной возможности задавать неограниченные по длине переменные, это свойство выглядит полезным.
Итак, формальные языки — это просто множества цепочек, составленных из символов некоторого конечного алфавита. Но возникает вопрос: как можно задать формальный язык? Если язык конечен, то можно просто выписать все его цепочки одну за другой (конечно, можно задуматься, имеет ли смысл выписывать цепочки языка, имеющего хотя бы десять тысяч элементов и, вообще, есть ли смысл в таком выписывании?). Что делать, если язык бесконечен, как его задавать? В этот момент на сцену выходят грамматики.
Формальные грамматики
Способ задания языка называет грамматикой этого языка. Таким образом, грамматикой мы называем любой способ задания языка. Например, грамматика L =
Назначение грамматики — задание языка. Это задание обязательно должно быть конечным, иначе человек не будет в состоянии эту грамматику понять. Но каким образом, конечное задание описывает бесконечные совокупности? Это возможно только в том случае, если строение всех цепочек языка основано на единых принципов, которых конечное число. В примере выше в качестве такого принципа выступает следующий: «каждая цепочка языка начинается с символов a, за которыми идет столько же символов b». Если язык представляет собой бесконечную совокупность случайным образом набранных цепочек, строение которых не подчиняется единым принципам, то очевидно для такого языка нельзя придумать грамматику. И здесь еще вопрос, можно или нет считать такую совокупность языком. В целях математической строгости и единообразия подхода обычно такие совокупности языком считают.
Итак, грамматика языка описывает законы внутреннего строения его цепочек. Такие законы обычно называют синтаксическими закономерностями. таким образом, можно перефразировать определение грамматики, как конечного способа описания синтаксических закономерностей языка. Для практики интересны не просто грамматики, но грамматики, которые могут быть заданы в рамках единого подхода (формализма или парадигмы). Иначе говоря, на основе единого языка (метаязыка) описания грамматик всех формальных языков. Тогда можно придумать алгоритм для компьютера, который будет брать на вход описание грамматики, сделанное на этом метаязыке, и что-то делать с цепочками языка.
Такие парадигмы описания грамматик называют синтаксическими теориями. Формальная грамматика — это математическая модель грамматики, описанная в рамках какой-то синтаксической теории. Таких теорий придумано довольно много. Самый известный метаязык для задания грамматик — это, конечно, порождающие грамматики Хомского. Но имеются и другие формализмы. Один из таких них — окрестностные грамматики, будет описан чуть ниже.
Окрестностные грамматики
В середине 60-х годов советский математик Юлий Анатольевич Шрейдер предложил простой способ описания синтаксиса языков на основе т.н. окрестностных грамматик. Для каждого символа языка задается конечное число его «окрестностей» — цепочек, содержащих данный символ (центр окрестности) где-то внутри. Набор таких окрестностей для каждого символа алфавита языка называется окрестностной грамматикой. Цепочка считается принадлежащей языку, задаваемому окрестностной грамматикой, если каждый символ этой цепочки входит в нее вместе с некоторой своей окрестностью.
Не всякий язык может быть описан окрестностной грамматикой. Рассмотрим, например, язык B, цепочки которого начинаются либо с символа «0», либо с символа «1». В последнем случае далее в цепочке могут идти символы «a» и «b». Если же цепочка начинается с нуля, то далее могут идти только символы «a». Нетрудно доказать, что для этого языка нельзя придумать никакой окрестностной грамматики. Легитимность вхождения символа «b» в цепочку обусловлена ее первым символом. Для любой окрестностной грамматики, в которой задается связь между символами «b» и «1» можно будет подобрать достаточно длинную цепочку, чтобы всякая окрестность символа «b» не доставала до начала цепочки. Тогда в начало можно будет подставить символ «0» и цепочка будет принадлежать языку A, что не отвечает нашим интуитивным представлениям о синтаксическом строении цепочек этого языка.
С другой стороны, легко можно построить конечный автомат, который распознает этот язык. Значит, класс языков, которые описываются окрестностными грамматиками, уже класса автоматных языков. Языки, задаваемые окрестностными грамматиками, будем называть шрейдеровскими. Таким образом, в иерархии языков можно выделить класс шрейдеровских языков, который является подклассом автоматных языков.
Можно сказать, что шрейдеровские языки задают одно простое синтаксическое отношение — «быть рядом» или отношение непосредственного предшествования. Отношение дальнего предшествования (которое, очевидно, присутствует в языке B) окрестностной грамматикой задано быть не может. Но, если визуализировать синтаксические отношения в цепочках языка, то для диаграмм отношений, в которые превращаются такие цепочки, можно придумать окрестностную грамматику.