Что значит эквивалентные множества

Эквивалентные множества

Мощность конечного множества

Мощностью конечного множества называют число элементов этого множества.

В общем случае мощность множества A обозначают |A|.

Для конечных множеств чаще встречается обозначение n(A).

Конечные множества легко сравнивать по мощности.

Если n(A) = n(B), то конечные множества A и B равномощны.

Например: Мощность множества A= <1;3;5;7>равна n(A)=4.

Мощность множества B = <-3;13;2;4>равна n(B) = 4.

Множества A и B равномощны.

Взаимно однозначное соответствие двух множеств

1) каждому элементу множества A соответствует только один элемент множества B;

2) каждый элемент множества B при этом соответствует некоторому элементу множества A;

3) разным элементам множества A соответствуют разные элементы множества B.

Каждый раз, когда мы «считаем» множество каких-то объектов, мы устанавливаем взаимно однозначно соответствие между этим множеством и подмножеством натуральных чисел от 1 до некоторого n.

С этой точки зрения утверждение

«У Толи три друга: Вася, Коля и Петя» выглядит как соответствие:

Эквивалентность

Такой подход даёт нам возможность сравнивать по мощности не только конечные, но и бесконечные (!) множества.

Сравним мощности множеств натуральных и натуральных чётных чисел:

Для мощности натуральных чисел используется специальное обозначение:

Счётные и несчётные множества

Чтобы доказать счётность множества достаточно придумать правило, по которому нумеруются его элементы.

Докажем, что множество целых чисел счётно.

Что и требовалось доказать.

Таким образом, множество отрезка [0;1]оказывается мощнее всего множества натуральных чисел.

Любой отрезок [a;b] и отрезок [0;1] эквивалентны.

Мощность любого действительного отрезка равна мощности континуума.

Чтобы доказать несчётность множества, нужно показать, что нет таких правил, по которым можно его посчитать. Это значительно сложнее, чем доказать счётность.

Примеры

Пример 1. Среди данных конечных множеств укажите пары эквивалентных:

Запишем с помощью перечисления:

$A \sim B, B \sim C, A \sim C$

В каждый треугольник можно вписать окружность, и притом только одну. Условие единственности (1) выполняется.

Вокруг каждой окружности можно описать бесконечное количество правильных треугольников, поворачивая их на некоторый угол относительно центра окружности.

Условие (2) не выполняется.

Соответствие не является взаимно однозначным.

Пример 3. Постройте взаимно однозначное соответствие между отрезком [0;1] и отрезком [2;7] с помощью линейной функции.

Искомая функция имеет вид y = kx+b, где

Прямая проходит через две точки: A(0;2),B(1;7).

Прямая проходит через две точки: A(0;a),B(1;b). Уравнение прямой:

Источник

Эквивалентность множеств

Определение 1.2. Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.

Эквивалентность множеств обозначается следующим образом: A

Эквивалентность множеств обладает следующим свойством транзитивности.

Докажем это свойство. Так как A

B, то для всякого элемента a Î А существует единственный элемент b Î B. Но так как B

C, то для всякого элемента b Î B существует единственный элемент c Î C. Сопоставим этот элемент элементу a Î А. Значит, для всякого элемента a Î А существует единственный элемент c Î C и для всякого элемента c Î C существует единственный элемент a Î А. Следовательно, A

Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = <4, 5, 6>и В = <x, y, z> эквивалентны, A

B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z.

Мощностью конечного множества А (обозначается çАç) называется число элементов этого множества. Например, мощность множества А = <1, 2>равна çАç= 2.

Рассмотрим задачу определения мощности объединения n конечных множеств.

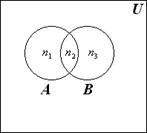
Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:

Из рис. 1.3 видим, что

Формула (1.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае

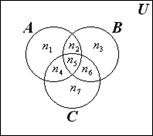
Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:

Из рис. 1.4 видим, что

что и доказывает формулу (1.2).

Формула (1.2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае

В общем случае мощность объединения n множеств определяется по формуле:

Эта формула выводится индукцией по n, [3].

Если множества А_i попарно не пересекаются, т.е. А_i ÇА_j = Æ, i ¹ j,то получим частный случай формулы (1.3):

В общем случае справедливо неравенство

Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = <1, 2, 3, …, n,…>, B = <– 1, –2, …, –n, …>. Тогда A

B. Взаимно однозначное соответствие устанавливается по правилу: элементу nÎ A соответствует элемент – nÎ B, т.е. n « – n.

B. Взаимно однозначное соответствие устанавливается по правилу: n « 2 n.

A = <1, 2, 3, …, n,…> – множество натуральных чисел, B = <…, –n, …– 2, –1, 0, 1, 2, …, n, …> – множество всех целых чисел.

Перепишем множество B следующим образом:

B = <0, –1, 1, – 2, 2, …, –n, n, …>, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n ³ 0 элементу a = 2n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2n из множества A (т.е. четному элементу) соответствует элемент b = –n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 « 0, 2 « –1, 3 « 1, 4 « –2 и т.д.

Примеры 1.18 и 1.19 показывают, что множество может быть эквивалентно своему подмножеству. Так, в примере 1.18 BÌ A, а в примере 1.19 A Ì B. И в том, и в другом случае A

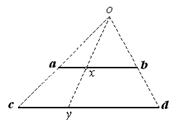
Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными путями. На рис. 1.5 показано, что множества точек двух отрезков [a, b] и [c, d] эквивалентны.

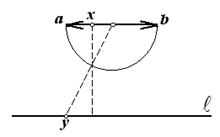
Таким же образом можно установить эквивалентность множеств точек двух интервалов. На рис.1.6 показано, что множества точек любого интервала (a, b) эквивалентно множеству точек всей прямой.

Для установления эквивалентности двух множеств можно применять следующую теорему.

Теорема Бернштейна. Если множество A эквивалентно части множества B, а множество B эквивалентно части множества A, то множества A и B эквивалентны.

Применим теорему Бернштейна для доказательства того, что множество точек любого отрезка эквивалентно множеству точек любого интервала.

Пусть A = [a, b] – произвольный отрезок, а B = (c, d) – произвольный интервал.

Таким образом, выполняются условия теоремы Бернштейна. Поэтому A

Итак, все интервалы, отрезки и вся прямая эквивалентны между собой.

Источник

Теория функций действительного переменного/Эквивалентные множества

Определение: Множество A называется эквивалентным множеству B, если существует биекция f:А→B. В этом случае говорят также, что множество A имеет одинаковую мощность с множеством B. Обозначение:A

Доказательство строится на определении эквивалентного множества и свойств биекции:

B₂,то A 1 × A 2 ∼ B 1 × B 2 <\displaystyle A_<1>\times A_<2>\sim B_<1>\times B_<2>> .

Tеорема 3: Пусть < A x >x ∈ X <\displaystyle \\>_> и < B y >y ∈ Y <\displaystyle \\>_> — два семейcтва попарно непересекающихся множеств, и пусть существует такая биекция: f:X→Y, что A_x

Tеорема 4: Если A 3 ⊂ A 2 ⊂ A 1 <\displaystyle A_<3>\subset A_<2>\subset A_<1>> и A₃

Понятие эквивалентности двух множеств было бы бессодержательным, если б оказалось, что все бесконечные множества эквивалентны между собой. Однако это не так, что и вытекает из следyщей теоремы.

Упражнения [ править ]

1. Установите биекцию между;

2. Доказать, что если A\B

6. Установите биекцию между

Источник

1.19 Эквивалентность множеств

Рассматривая различные множества, можно заметить, что иногда можно указать число элементов в данном множестве. Таковы, напри­мер, множества всех вершин многогранника, жителей Харькова и т. д. Каждое из этих множеств содержит конечное число элементов. С дру­гой стороны, есть множества, состоящие из бесконечного числа элемен­тов, например, множество натуральных чисел, множество точек отрезка и т. д. При этом, говоря, что множество бесконечно, мы имеем в виду тот факт, что из него можно извлекать любое количество элементов и после каждого извлечения в этом множестве остаются элементы.

При изучении множеств естественным образом возникает вопрос о способах сравнения двух множеств: одинаковое число элементов в них или в одном множестве элементов больше, чем в другом. Два ко­нечных множества сравнить между собой нетрудно. Но имеет ли смысл сравнивать два бесконечных множества? Есть ли смысл в вопросе: «чего больше – точек на отрезке [0; 1] или элементов в множестве натуральных чисел?». Если имеет, то надо предложить способ сравнения двух бесконечных множеств. Посмотрим, как сравнивают между собой два конечных множества.

Например, мы сравним количество студентов в аудитории с ко­личеством стульев. Очевидно, что такое сравнение можно осуществить двумя способами:

Во-первых, можно сосчитать число студентов и число стульев и таким образом сравнить число элементов в этих множествах.

Во-вторых, можно поступить иначе – не пересчитывать ни сту­дентов, ни стульев, а просто посадить студентов на стулья. И сразу все станет ясно. Если число элементов в этих множествах одинаково, то не останется ни стоящих студентов, ни лишних стульев. Если говорить строгим языком математики, то во втором случае мы установили взаимно-однозначное соответствие между элементами двух множеств, при котором одному элементу из множества студентов Соответствует один и только один элемент из множества стульев и – наоборот. Это отношение называется Биекцией. Совершенно очевидно, что установить биекцию можно лишь тогда, когда число элементов в двух множествах одинаково. Этот способ пригоден для сравнения бесконечных мно­жеств. Говорить о равенстве чисел элементов бесконечных множеств некорректно. Поэтому вводится понятие эквивалентности.

Два множества M и N называются Эквивалентными (M

N),если между элементами этих множеств можно установить взаимно-одно­значное соответствие (Биекцию).

Понятие эквивалентности применимо к любым множествам. Два конечных множества эквивалентны между собой тогда и только тогда, когда число элементов в них одинаково.

Так как для отношения эквивалентности выполняется свойство Транзитивности, то совершенно очевидно, что если два множества эк­вивалентны третьему, то они эквивалентны между собой.

Рис. 1.13 – Пример эквивалентности двух множеств

Пример. Множества точек любых двух отрезков [A; B] и [С; D] эквивалентны между собой. Из рис.1 ясно, как между ними установить биекцию. Ведь любые две точки P и Q соответствуют друг другу, если они являются проекциями одной и той же точки R вспомогательного отрезка [E; F].

Говорить о количестве элементов бесконечного множества бес­смысленно. Поэтому вводится понятие Мощности множества. Гово­рят, что два эквивалентные между собой бесконечные множества имеют Одинаковую мощность. Для конечных множеств понятие мощ­ности совпадает с привычным понятием числа элементов.

Источник

Что значит эквивалентные множества

1.5. Эквивалентность множеств. Мощность множеств

Если каждому элементу множества А можно по некоторому правилу поставить в соответствие один и только один элемент множества В и, наоборот, каждому элементу множества В по некоторому правилу можно поставить в соответствие один и только один элемент множества А, то говорят, что между элементами множеств А и В установлено взаимно однозначное соответствие. В этом случае множества А и В называют эквивалентными и записывают: А

Очевидно, что равночисленные множества эквивалентны. И, наоборот, два эквивалентных конечных множества равночисленны.

Этот факт является логически чрезвычайно важным, так как для установления равночисленности конечных множеств нет необходимости обладать понятием натурального числа, с помощью которого мы подсчитываем элементы множеств. Напротив, теперь само понятие натурального числа получает новую трактовку: оно есть количественная характеристика, общая всем эквивалентным между собой конечным множествам. Теперь можно, пользуясь только понятиями «множество», «принадлежность», «взаимно однозначное соответствие» построить всю теорию натуральных чисел.

Рассмотрим теперь бесконечные множества. Для сравнения бесконечных множеств нельзя использовать понятие натурального числа, ибо нельзя пересчитать все элементы таких множеств и поставить им в соответствие натуральное число. Однако их можно сравнивать при помощи понятий «взаимно однозначное соответствие», «эквивалентность».

N и множество целых отрицательных чисел является счетным.

Если для конечных эквивалентных множеств мы говорили, что они равночисленны, то о бесконечных множествах будем говорить, что они равномощны, т.е. имеют одинаковую мощность. Все эквивалентные бесконечные множества характеризуются их мощностью.

Понятие мощности бесконечного множества аналогично понятию числа конечного множества. Мощность – обобщение понятия «количество» для бесконечных множеств. Оно позволяет сравнивать различные бесконечные множества.

Между двумя мощностями бесконечных множеств можно устанавливать отношения: «равенство», «больше», «меньше». Это дает основание назвать символы, обозначающие мощности бесконечных множеств, считать «числами». Георг Кантор назвал такие «числа» кардинальными (в отличие от натуральных), подчеркивая тем самым, что область определенных величин не исчерпывается конечными величинами. Понятие кардинального числа есть расширение, обобщение понятия числа вообще. Расширение понятия числа в область бесконечного означает переход математического мышления к качественно-новому этапу его развития.

Источник