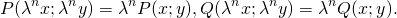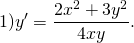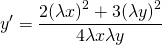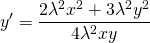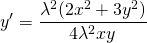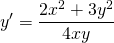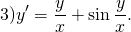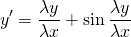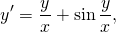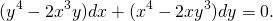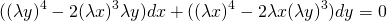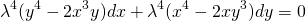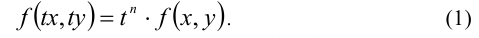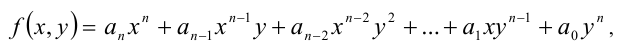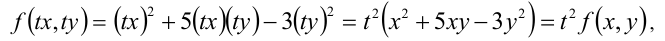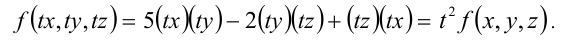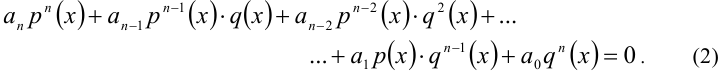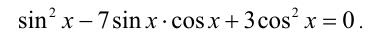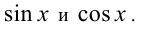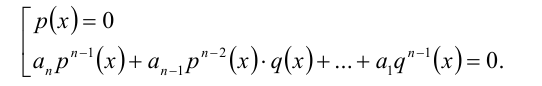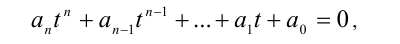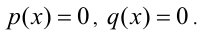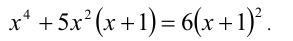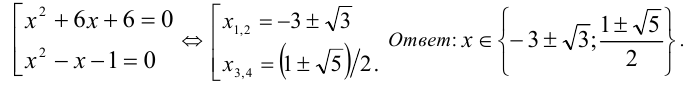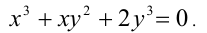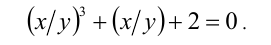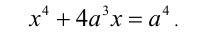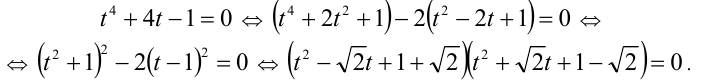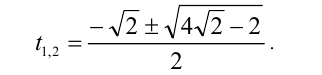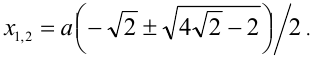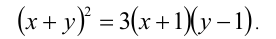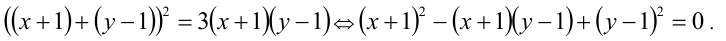Что значит что уравнение однородное

10.04.202211.04.2022 admin 0 Comments

Как определить однородное уравнение

Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть

Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.

Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).

Подставляем вместо каждого x λx, вместо каждого y — λy:

Выносим лямбда в квадрате за скобки и сокращаем на него:

Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.

2) (x-y)ydx-x²dy=0.

Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:

(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).

Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:

После сокращения на λ получаем исходное уравнение:

а это значит, что данное уравнение является однородным.

Подставляем вместо каждого x λx, вместо каждого y — λy:

Делим обе части уравнения на лямбда в 4й степени:

Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).

Источник

Однородное уравнение

Смотреть что такое «Однородное уравнение» в других словарях:

однородное уравнение — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN homogeneous equation … Справочник технического переводчика

Однородное уравнение — Однородным уравнением n й степени, называется уравнение вида: Такое уравнение после исключения отдельно рассматриваемого случая и деления уравнения на сводится с помощью замены к алгебраическому уравнению … Википедия

Уравнение Коши — Эйлера — В математике ( дифференциальных уравнениях), уравнение Коши Эйлера (Эйлера Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному уравнению с… … Википедия

Уравнение теплопроводности — Пример численного решения уравнения теплопроводности. Цветом и высотой поверхности передана температура данной точки. Уравнение теплопроводности важное уравнение в частных производных, которое описывает распространение тепла в заданной… … Википедия

Уравнение Коши — В математике (дифференциальных уравнениях), уравнение Коши Эйлера (Эйлера Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному… … Википедия

Уравнение диффузии — Механика сплошных сред … Википедия

Линейное дифференциальное уравнение с постоянными коэффициентами — Линейное дифференциальное уравнение с постоянными коэффициентами обыкновенное дифференциальное уравнение вида: где искомая функция, её тая производная, фиксированные числа … Википедия

Источник

Что значит что уравнение однородное

Однородное дифференциальное уравнение можно решить с помощью подстановки \(y = ux,\) которая преобразует однородное уравнение в уравнение с разделяющимися переменными.

Дифференциальное уравнение вида \[\left( <x + y + > \right)dx + \left( <x + y + > \right)dy = 0\] преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной: \[z = ax + by.\]

Нетрудно заметить, что многочлены \(P\left( \right)\) и \(Q\left( \right),\) соответственно, при \(dx\) и \(dy,\) являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным.

Интегрируем последнее выражение: \[\int = 2\int <\frac<>> \;\;\text<или>\;\;u = 2\ln \left| x \right| + C,\] где \(C\) − постоянная интегрирования.

Возвращаясь к старой переменной \(y,\) можно записать: \[y = ux = x\left( <2\ln \left| x \right| + C>\right).\] Таким образом, уравнение имеет два решения: \[y = x\left( <2\ln \left| x \right| + C>\right),\;\;x = 0.\]

Заметим, что корень \(x = 0\) не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме: \[y’ = \frac\ln \frac = f\left( <\frac> \right).\] Как видно, уравнение является однородным.

Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде: \[ >><>> > = <\frac<<\frac<<>><<>>>><<\frac<><<>> + \frac<<>><<>>>> > = <\frac<<<<\left( <\frac> \right)>^2>>><<\frac + <<\left( <\frac> \right)>^2>>> > = > \right).> \] Сделаем подстановку \(y = ux.\) Тогда \(y’ = u’x + u.\) Подставляя \(y\) и \(y’\) в исходное уравнение, получаем: \[ <\left( > \right)\left( \right) = ,>\;\; <\Rightarrow u\left( \right)\left( \right) = .> \] Разделим обе части уравнения на \(u.\) Заметим, что корень \(x = 0\) не является решением, но можно убедиться, что корень \(u = 0\) (или \(y = 0\)) будет одним из решений данного дифференциального уравнения.

Источник

Однородные уравнения

Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде

где 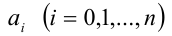— коэффициенты многочлена, одновременно не обращающиеся в нуль.

т.е. условие (1) из определения выполняется (n = 2).

Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.

Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, .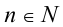

В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида

Оно является однородным тригонометрическим уравнением 2-й степени относительно функций

Перейдём к процедуре решения уравнения (2).

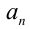
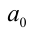
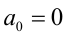
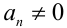
Если хотя бы один из коэффициентов или обращается в нуль, то левая часть уравнения легко раскладывается на множители. В результате уравнение оказывается равносильно на ОДЗ совокупности двух уравнений. Например, если , то получим совокупность

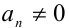
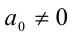
Если же и , то для решения однородного уравнения (2) необходимо рассмотреть два возможных случая.

решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.

2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений

Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.

Пример №185.

Решить уравнение

Решение:

Пример №186.

Решить в целых числах уравнение

Решение:

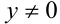
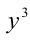
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть , тогда поделим обе части уравнения на :

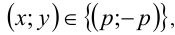
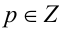
Ответ: где .

Пример №187.

Для каждого действительного значения параметра а решить уравнение

Решение:

Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.

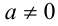
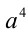
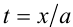
2) Если , то поделим на , и положим :

Первый сомножитель в нуль не обращается, а второй имеет два корня

Ответ: при а = 0 единственное решение x = 0 ;

при 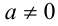два решения

Пример №188.

Найти действительные корни уравнения

Решение:

Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду

Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.

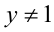
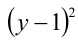
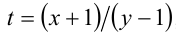
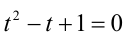
1) Если , то, поделив на и обозначив , получим нет решений.

Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник

Однородное уравнение

Одноро́дным уравнением n-й степени, называется уравнение вида:

Такое уравнение после исключения отдельно рассматриваемого случая и деления уравнения на сводится с помощью замены к алгебраическому уравнению -ой степени

См. также

Полезное

Смотреть что такое «Однородное уравнение» в других словарях:

Однородное уравнение — уравнение, не меняющее своего вида при одновременном умножении всех (или только некоторых) неизвестных на одно и то же произвольное число. Во втором случае уравнение называется однородным по отношению к соответствующим неизвестным. Так,… … Большая советская энциклопедия

Уравнение диффузии — Механика сплошных сред … Википедия

Источник

Что и для чего?

Что значит что уравнение однородное

Как определить однородное уравнение

Однородное уравнение

Смотреть что такое «Однородное уравнение» в других словарях:

Что значит что уравнение однородное

Однородные уравнения