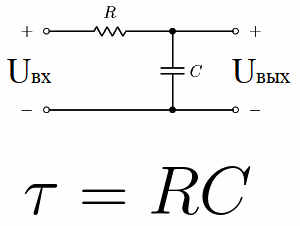Что означает термин постоянная времени

Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.

Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.

Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.

Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.

Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.

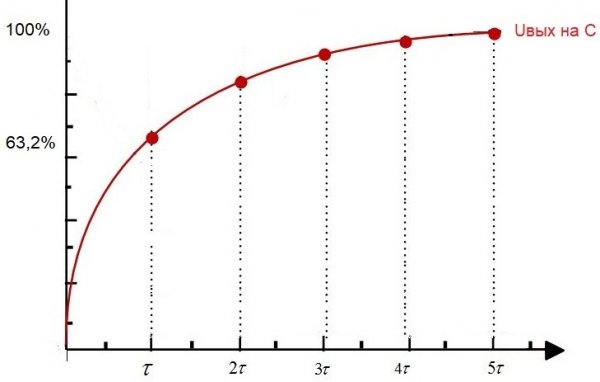
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.

Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.

Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.

Интегрирующие RC-цепи применяются в электронике в качестве фильтров нижних частот, когда более высокие частоты необходимо отсечь (подавить), а более низкие — пропустить.

Практически механизм такой фильтрации зиждиться на следующем принципе. Для переменного тока конденсатор выступает как емкостное сопротивление, значение которого обратно пропорционально частоте, то есть чем выше частота — тем меньшим будет реактивное сопротивление конденсатора в омах.

Следовательно, если пропустить через RC-цепь переменный ток, то, как на плечах делителя напряжения, на конденсаторе упадет определенное напряжение, пропорциональное его емкостному сопротивлению на частоте пропускаемого тока.

Если известна частота среза и амплитуда входного переменного сигнала, то для разработчика не составит труда подобрать такие конденсатор и резистор в RC-цепь, чтобы минимальное (граничное) напряжение (для частоты среза — верхней частотной границы) приходилось на конденсатор как на реактивное сопротивление, входящее в состав делителя в совокупности с резистором.

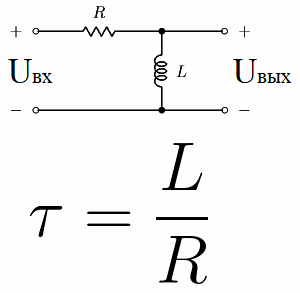
Теперь рассмотрим так называемую дифференцирующую цепь. Это цепь, состоящая из последовательно соединенных резистора и катушки индуктивности, RL-цепь. Ее постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.

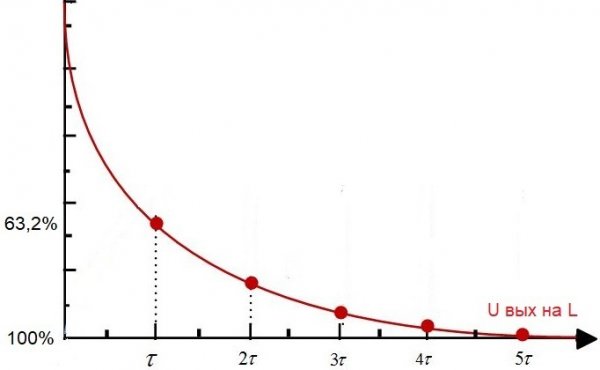
Если к такой цепи приложить постоянное напряжение от источника, то через время тау напряжение на катушке уменьшится по сравнению с U вх на 63,2%, то есть в полном соответствии со значением постоянной времени для данной электрической цепи.

В цепях переменного тока (переменных сигналов) LR-цепи применяются в качестве фильтров верхних частот, когда низкие частоты необходимо отсечь (подавить), а частоты выше (выше частоты среза — нижней частотной границы)— пропустить. Так вот, индуктивное сопротивление катушки тем больше, чем выше частота.

Как и в случае с рассмотренной выше RC-цепью, здесь используется принцип делителя напряжения. Ток более высокой частоты, пропускаемый через RL-цепь, вызовет большее падение напряжения на индуктивности L, как на индуктивном сопротивлении, входящем в состав делителя напряжения в совокупности с резистором. Задача разработчика — подобрать такие R и L, чтобы минимальное (граничное) напряжение на катушке получалось как раз на частоте среза.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Источник

Постоянная времени

Полезное

Смотреть что такое «Постоянная времени» в других словарях:

ПОСТОЯННАЯ ВРЕМЕНИ — величина, характеризующая инерционность динамической системы; имеет размерность времени. Напр., постоянная времени электрической цепи характеризует скорость изменения тока или напряжения в ней при переходном процессе … Большой Энциклопедический словарь

постоянная времени — процесса в разрядном промежутке; постоянная времени Время, в течение которого какой либо определяющий параметр процесса, протекающего в разрядном промежутке, достигает заданной доли от разности между начальным и конечным значениями этого… … Политехнический терминологический толковый словарь

постоянная времени — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN time constant … Справочник технического переводчика

постоянная времени — 3.2 постоянная времени: Величина, характеризующая инерционность динамической системы при изменении регистрируемого сигнала по экспоненциальному закону. Источник: ГОСТ Р 53375 2009: Скважины нефтяные и газовые. Геолого технологические исследования … Словарь-справочник терминов нормативно-технической документации

Постоянная времени — См. также: Постоянная времени (нейрофизиология) Постоянная времени характеристика экспоненциального процесса, определяющая время, через которое амплитуда процесса упадёт в «е» раз. В радиотехнике В радиотехнике постоянная времени… … Википедия

постоянная времени — величина, характеризующая инерционность динамической системы; имеет размерность времени. Например, постоянная времени электрической цепи характеризует скорость изменения тока или напряжения в ней при переходном процессе. * * * ПОСТОЯННАЯ ВРЕМЕНИ… … Энциклопедический словарь

Постоянная времени — 120) постоянная времени время, отсчитываемое с момента приложения светового воздействия, которое требуется току, чтобы достигнуть уровня (1 1/е) от конечного значения (то есть 63% от конечного значения) (категория 6);. Источник: Приказ ФТС… … Официальная терминология

постоянная времени — laiko pastovioji statusas T sritis automatika atitikmenys: angl. time constant vok. Zeitkonstante, f rus. постоянная времени, f pranc. constante de temps, f … Automatikos terminų žodynas

постоянная времени — vyksmo trukmės konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Laiko tarpas, per kurį pereinamąjį vyksmą apibūdinantis parametras pakinta e (e = 2,71828…) kartų. atitikmenys: angl. time constant vok. Zeitkonstante, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

постоянная времени — trukmės konstanta statusas T sritis fizika atitikmenys: angl. time constant vok. Zeitkonstante, f rus. постоянная времени, f pranc. constante de temps, f … Fizikos terminų žodynas

постоянная времени — [time constant] обобщенный параметр, характеризующий динамические свойства (инерционность) объекта исследования и имеющий размерность времени. Ппостоянная времени широко используется при расчете динамики разных объектов исследования (процессов).… … Энциклопедический словарь по металлургии

Источник

Постоянная времени

Передаточная функция в представлении постоянной времени возникает следующим образом:

оглавление

Определение постоянных времени по полиномам линейной динамической системы передачи высшего порядка

Пример обыкновенного дифференциального уравнения высшего порядка системы передачи с постоянными коэффициентами и : а я <\ displaystyle a_ > б я <\ displaystyle b_ >

Эта общая форма дифференциального уравнения подвергается преобразованию Лапласа:

Передаточная функция G (s) формируется из отношения выходной переменной к входной. Не должно быть начальных значений внутреннего накопителя энергии ( представления в пространстве состояний ) системы.

Для определения постоянных времени полиномы передаточной функции разбиваются на линейные множители и множители 2-го порядка путем определения нулей. Если числовые значения даны для коэффициентов многочленов, многочлены могут быть факторизованы путем определения корней.

Разложение полиномов числителя и знаменателя более высокого порядка по полюсам и нулям приводит к множеству линейных множителей и множеству множителей 2-го порядка. В качестве предпосылки для этого многочлены не должны иметь пробелов в порядке элементов суммы согласно порядковому номеру.

Если эти факторы определены как независимые индивидуальные передаточные функции, в зависимости от типа полюсов и нулей возникают следующие элементарные передаточные функции:

Пример передаточной функции с полиномиальным представлением, представлением полюс-нуль и представлением постоянной времени:

Постоянные времени элементарных индивидуальных систем в числителе и знаменателе передаточной функции

Установление и поведение элементарных индивидуальных систем

Дифференцирующие элементы могут полностью компенсировать поведение замедляющих элементов во времени с теми же постоянными времени. То же самое, конечно, относится к ссылкам и ссылкам. П. Д. 1 <\ displaystyle PD_ <1>> П. Т 1 <\ displaystyle PT_ <1>> П. Д. 2 <\ displaystyle PD_ <2>> П. Т 2 <\ displaystyle PT_ <2>>

Тестовые сигналы для проверки поведения системы:

Временной ход дифференцирующих передаточных элементов:

Временной ход передаточных элементов с комплексно сопряженными полюсами ( элементами): П. Т 2 k k <\ displaystyle PT_ <2kk>>

Системы передачи с линейными коэффициентами или коэффициентами 2-го порядка с положительной действительной частью полюсов:

Положительные действительные части полюсов и нулей приводят к отрицательным постоянным времени.

Расчет временного поведения передаточных функций

Тестовые сигналы

Непериодические (детерминированные) тестовые сигналы имеют центральное значение в теории систем. С их помощью можно протестировать трансмиссионную систему, проверить ее устойчивость или определить свойства.

Основы определения постоянных времени из обыкновенного дифференциального уравнения первого порядка

Линейное обыкновенное дифференциальное уравнение 1-го порядка с постоянными коэффициентами и гласит: а я <\ displaystyle a_ > б я <\ displaystyle b_ >

у ˙ ( т ) + а 0 а 1 ⋅ у ( т ) знак равно б 0 а 1 ⋅ ты ( т ) <\ displaystyle <\ dot > (t) + <\ frac > >> \ cdot y (t) = <\ frac > >> \ cdot u (t)> .

Передаточная функция G (s) этого дифференциального уравнения читается для начальных условий, равных нулю, после применения теоремы о дифференцировании Лапласа:

s ⋅ Y ( s ) + а 0 а 1 ⋅ Y ( s ) знак равно б 0 а 1 ⋅ U ( s ) <\ displaystyle s \ cdot Y (s) + <\ frac > >> \ cdot Y (s) = <\ frac > >>) \ cdot U (s)> .

Если вы вставите для и в уравнение передаточной функции, вы получите нормальную форму передаточной функции элемента ( элемента) задержки в представлении постоянной времени: а 1 а 0 знак равно Т <\ displaystyle <\ frac > >> = T> б 0 а 0 знак равно K <\ displaystyle <\ frac > >> = K> П. Т 1 <\ displaystyle PT_ <1>>

Построение обыкновенного дифференциального уравнения первого порядка из аппаратного ФНЧ.

Для аппаратной модели в качестве фильтра нижних частот применяется сеточное уравнение напряжений:

Р. ⋅ С. ⋅ d U С. d т + U С. знак равно U е <\ Displaystyle R \ cdot C \ cdot <\ frac >

> + U_ = U_ >

у ˙ ( т ) + 1 Р. ⋅ С. ⋅ у ( т ) знак равно 1 Р. ⋅ С. ⋅ ты ( т ) <\ displaystyle <\ dot > (t) + <\ frac <1>> \ cdot y (t) = <\ frac <1>> \ cdot u (t)>

Передаточная функция G (s) этого дифференциального уравнения читается для начальных условий, равных нулю, согласно теореме дифференцирования:

Суммированная как отношение выходных переменных к входной, передаточная функция приводит к представлению постоянной времени:

Если емкость C заменяется индуктивностью L в RC-цепи, создается фильтр верхних частот первого порядка при рассмотрении входных и выходных напряжений системы. В случае высокочастотных входных сигналов индуктивность имеет высокое комплексное сопротивление. С падением частоты индуктивное сопротивление падает.

Расчет временного поведения элемента после входного скачка П. Т 1 <\ displaystyle PT_ <1>>

Пример расчета для определения постоянных времени обыкновенного дифференциального уравнения 2-го порядка

Требуются: передаточная функция, полюса, постоянные времени.

Применение преобразования Лапласа дифференциального уравнения согласно теореме дифференцирования:

В Интернете (Google) есть программы, которые могут вычислять нули многочленов до 4-го порядка.

Так называемая формула pq может использоваться для решения нулей (полюсов) многочлена 2-го порядка:

Это позволяет факторизовать полином и передаточную функцию в представлении постоянной времени.

Эти уравнения алгебраически идентичны.

Аппаратное моделирование этой системы с двумя последовательно включенными RC-элементами требует развязки без нагрузки.

Расчет временного поведения передаточной функции более высокого порядка сложной динамической системы для заданной входной переменной состоит из:

Источник

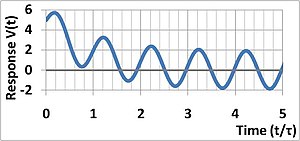
В физика и инженерное дело, то постоянная времени, обычно обозначаемый Греческий буква τ (тау), это параметр характеризующий реакцию на ступенчатый вход первого порядка, линейный инвариантный во времени (LTI) система. [1] [примечание 1] Постоянная времени является основным характеристическая единица системы LTI первого порядка.

Содержание

Дифференциальное уравнение

Системы LTI первого порядка характеризуются дифференциальным уравнением

где τ представляет экспоненциальный спад постоянный и V это функция времени т

то импульсная функция, часто обозначаемый δ (t), а также функция синусоидального входа:

Пример решения

Пример решения дифференциального уравнения с начальным значением V₀ и нет функции принуждения

начальное значение V. Таким образом, отклик представляет собой экспоненциальный спад с постоянной времени. τ.

Обсуждение

Конкретные случаи

Связь постоянной времени с полосой пропускания

Предположим, что функция принуждения выбрана синусоидальной, поэтому:

(Отклик на входную реальную косинусную или синусоидальную волну можно получить, взяв действительную или мнимую часть конечного результата в силу Формула Эйлера.) Общее решение этого уравнения для времен т ≥ 0 с, полагая V (t = 0) = V₀ является:

В течение долгого времени убывающие экспоненты становятся незначительными и устойчивое состояние раствор или долгосрочное решение:

Величина этого ответа:

Обозначение ж_{3 дБ} проистекает из выражения власти в децибелы и наблюдение, что половинная мощность соответствует падению значения | V_∞| на коэффициент 1 / √2 или на 3 децибела.

Таким образом, постоянная времени определяет полосу пропускания этой системы.

Переходная характеристика с произвольными начальными условиями

Предположим, что функция принуждения выбрана в качестве пошагового входа, поэтому:

с участием u (t) ступенчатая функция Хевисайда. Общее решение этого уравнения для времен т ≥ 0 с, предполагая V (t = 0) = V₀ является:

(Можно заметить, что этот отклик является пределом ω → 0 вышеуказанного отклика на синусоидальный вход.)

Долгосрочное решение не зависит от времени и начальных условий:

Постоянная времени остается неизменной для той же системы независимо от условий запуска. Проще говоря, система приближается к своему окончательному, установившемуся состоянию с постоянной скоростью, независимо от того, насколько близко она к этому значению в любой произвольной начальной точке.

Например, рассмотрим электродвигатель, запуск которого хорошо моделируется системой LTI первого порядка. Предположим, что при запуске из состояния покоя двигателю требуется секунды, чтобы достичь 63% своей номинальной скорости 100 об / мин, или 63 об / мин, то есть меньше 37 об / мин. Тогда будет обнаружено, что после следующих секунды двигатель ускорился еще на 23 об / мин, что составляет 63% от этой разницы в 37 об / мин. Это доводит его до 86 об / мин, что все еще составляет 14 об / мин. Через треть ⅛ секунды двигатель наберет дополнительные 9 оборотов в минуту (63% от этой разницы в 14 оборотов в минуту), установив его на 95 оборотов в минуту.

Примеры

Постоянные времени в электрических цепях

где р сопротивление (в Ом) и C это емкость (в фарады).

Электрические схемы часто более сложны, чем эти примеры, и могут иметь несколько постоянных времени (см. Шаговый ответ и Расщепление полюсов для некоторых примеров.) В случае, когда Обратная связь присутствует, система может демонстрировать неустойчивые, увеличивающиеся колебания. Вдобавок физические электрические цепи редко являются действительно линейными системами, за исключением возбуждений с очень низкой амплитудой; однако широко используется приближение линейности.

Тепловая постоянная времени

где час это коэффициент теплопередачи, и А_s площадь поверхности, Т (т) = температура тела во время т, и Т_а постоянная температура окружающей среды. Положительный знак указывает на соглашение, что F положительно, когда тепло уходящий тело, потому что его температура выше, чем температура окружающей среды (F это внешний поток). Если тепло теряется в окружающую среду, эта теплопередача приводит к падению температуры тела, определяемому: [5]

где ρ = плотность, c_п = удельная теплоемкость и V объем тела. Отрицательный знак указывает на падение температуры при теплопередаче. наружу от тела (то есть когда F > 0). Приравнивая эти два выражения для теплопередачи,

Очевидно, это LTI-система первого порядка, которую можно представить в виде:

Другими словами, постоянная времени говорит, что большие массы ρV и большей теплоемкости c_п приводят к более медленным изменениям температуры, в то время как большие площади поверхности А_s и лучшая теплопередача час приводят к более быстрым изменениям температуры.

Говорят, что системы, для которых охлаждение удовлетворяет приведенному выше экспоненциальному уравнению, удовлетворяют Закон охлаждения Ньютона. Решение этого уравнения предполагает, что в таких системах разница между температурой системы и окружающей среды ΔT как функция времени т, дан кем-то:

где ΔT₀ начальная разница температур в момент времени т = 0. На словах, тело принимает ту же температуру, что и окружающая среда, с экспоненциально медленной скоростью, определяемой постоянной времени.

Константы времени в нейробиологии

где р_м сопротивление через мембрану и c_м это емкость мембраны.

Сопротивление мембраны зависит от количества открытых ионные каналы а емкость зависит от свойств липидный бислой.

Постоянная времени используется для описания роста и падения мембранного напряжения, где рост описывается выражением

V ( т ) = V Максимум ( 1 − е − т / τ ) > (1-e ^ <- t / au>)>

и падение описывается

V ( т ) = V Максимум е − т / τ > e ^ <- t / au>>

V_{Максимум} определяется как максимальное изменение напряжения от потенциал покоя, где

Чем больше постоянная времени, тем медленнее растет или падает потенциал нейрона. Длительная постоянная времени может привести к временное суммирование, или алгебраическое суммирование повторяющихся потенциалов. Короткая постоянная времени скорее дает детектор совпадений через пространственное суммирование.

Экспоненциальный спад

Метеорологические датчики

Чаще всего это относится к измерениям температуры, температуры точки росы, влажности и давления воздуха. Радиозонды особенно страдают из-за их быстрого увеличения высоты.

Источник