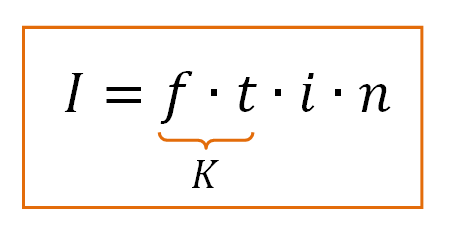Что означает частота сигнала в 70 гц информатика
Частота, период сигнала, изменения напряжения, силы тока. Периодический. Единицы измерения. Герц, Гц, Hz. Hertz. Доли. килогерц, кгц, мегагерц, мгц
Понятие частоты и периода периодического сигнала. Единицы измерения. (10+)
Частота и период сигнала. Понятие. Единицы измерения
Материал является пояснением и дополнением к статье:
Единицы измерения физических величин в радиоэлектронике
Единицы измерения и соотношения физических величин, применяемых в радиотехника.
В природе нередко встречаются периодические процессы. Это означает, что какой-то параметр, характеризующий процесс, изменяется по периодическому закону, то есть верно равенство:
Определение частоты и периода
Понятно, что если верно предыдущее равенство, то верно и такое:
В радиоэлектронике мы исследуем силу тока и напряжение, так что периодическими сигналами будем считать сигналы, для напряжения или силы тока в которых верно соотношение 1.
Вашему вниманию подборка материалов:
Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам
Единицы измерения частоты и периода
Частота измеряется, соответственно, в 1 / секунда. Эту единицу измерения еще называют Герц (Hertz) и обозначают Гц (Hz). В зарубежной литературе можно встретить и такое обозначение ‘cycles per second’ (cps).
В природе много видов периодических сигналов. Наиболее распространены синусоидальные, прямоугольные (меандр), треугольные, пилообразные и т. д. Распространены и непериодические сигналы: шум, затухающие колебания, модулированные сигналы.
Частота и период непериодических сигналов
Вообще говоря понятия периода и частоты применимы только к периодическим сигналам. Но в электронике иногда их условно применяют к непериодическим сигналам, например, к затухающим колебаниям, сигналам с амплитудной и широтно-импульсной модуляцией. Это возможно, когда функция зависимости напряжения сигнала от времени может быть представлена, как суперпозиция двух функций, периодической (U2) и непериодической (U1):
Тогда считают, что частота и период итогового сигнала равны частоте и периоду U2.
Например, для затухающих синусоидальных колебаний, амплитуда которых падает обратно-пропорционально времени, формула будет иметь вид:
Единицы измерения, кратные Герцу (Hertz)
Приведем единицы измерения, кратные Герц, чаще всего применяемые в электронике.
| Гигагерц | ГГц | GHz | 1E9 Гц | 1000000000 Гц |
| Мегагерц | МГц | MHz | 1E6 Гц | 1000000 Гц |
| Килогерц | кГц | kHz | 1E3 Гц | 1000 Гц |
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.
Мобильное управление освещением. Звуковое реле. Включение / выключение.
Звуковое реле и схемы для включения освещения с помощью звонка на мобильный теле.
Герц (единица измерения)
10 Гц — десять исполнений такого процесса, или десять колебаний за одну секунду.
История
Назван в честь немецкого учёного-физика XIX века Генриха Герца, который внёс важный вклад в развитие электродинамики. Название было учреждено Международной электротехнической комиссией в 1930 году. В 1960 году на генеральной конференции по мерам и весам это название было принято взамен ранее существовавшего термина (число циклов в секунду).
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 Гц | декагерц | даГц | daHz | 10 −1 Гц | децигерц | дГц | dHz |
| 10 2 Гц | гектогерц | гГц | hHz | 10 −2 Гц | сантигерц | сГц | cHz |
| 10 3 Гц | килогерц | кГц | kHz | 10 −3 Гц | миллигерц | мГц | mHz |
| 10 6 Гц | мегагерц | МГц | MHz | 10 −6 Гц | микрогерц | мкГц | µHz |
| 10 9 Гц | гигагерц | ГГц | GHz | 10 −9 Гц | наногерц | нГц | nHz |
| 10 12 Гц | терагерц | ТГц | THz | 10 −12 Гц | пикогерц | пГц | pHz |
| 10 15 Гц | петагерц | ПГц | PHz | 10 −15 Гц | фемтогерц | фГц | fHz |
| 10 18 Гц | эксагерц | ЭГц | EHz | 10 −18 Гц | аттогерц | аГц | aHz |
| 10 21 Гц | зеттагерц | ЗГц | ZHz | 10 −21 Гц | зептогерц | зГц | zHz |
| 10 24 Гц | йоттагерц | ИГц | YHz | 10 −24 Гц | йоктогерц | иГц | yHz |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Примеры
Полезное
Смотреть что такое «Герц (единица измерения)» в других словарях:
Единица измерения Сименс — Сименс (обозначение: См, S) единица измерения электрической проводимости в системе СИ, величина обратная ому. До Второй мировой войны (в СССР до 1960 х годов) сименсом называлась единица электрического сопротивления, соответсвующая сопротивлению … Википедия
Беккерель (единица измерения) — У этого термина существуют и другие значения, см. Беккерель. Беккерель (обозначение: Бк, Bq) единица измерения активности радиоактивного источника в Международной системе единиц (СИ). Один беккерель определяется как активность источника, в… … Википедия
Свеча (единица измерения) — Кандела (обозначение: кд, cd) одна из семи основных единиц измерения системы СИ, равна силе света, испускаемого в заданном направлении источником монохроматического излучения частотой 540·1012 герц, энергетическая сила света которого в этом… … Википедия
Зиверт (единица измерения) — Зиверт (обозначение: Зв, Sv) единица измерения эффективной и эквивалентной доз ионизирующего излучения в Международной системе единиц (СИ), используется с 1979 г. 1 зиверт это количество энергии, поглощённое килограммом… … Википедия
Ньютон (единица измерения) — У этого термина существуют и другие значения, см. Ньютон. Ньютон (обозначение: Н) единица измерения силы в Международной системе единиц (СИ). Принятое международное название newton (обозначение: N). Ньютон производная единица. Исходя из второго… … Википедия
Сименс (единица измерения) — У этого термина существуют и другие значения, см. Сименс. Сименс (русское обозначение: См; международное обозначение: S) единица измерения электрической проводимости в Международной системе единиц (СИ), величина обратная ому. Через другие… … Википедия
Паскаль (единица измерения) — У этого термина существуют и другие значения, см. Паскаль (значения). Паскаль (обозначение: Па, международное: Pa) единица измерения давления (механического напряжения) в Международной системе единиц (СИ). Паскаль равен давлению… … Википедия
Тесла (единица измерения) — У этого термина существуют и другие значения, см. Тесла. Тесла (русское обозначение: Тл; международное обозначение: T) единица измерения индукции магнитного поля в Международной системе единиц (СИ), численно равная индукции такого… … Википедия
Грей (единица измерения) — У этого термина существуют и другие значения, см. Грей. Грей (обозначение: Гр, Gy) единица измерения поглощённой дозы ионизирующего излучения в Международной системе единиц (СИ). Поглощённая доза равна одному грею, если в результате… … Википедия
Вебер (единица измерения) — У этого термина существуют и другие значения, см. Вебер. Вебер (обозначение: Вб, Wb) единица измерения магнитного потока в системе СИ. По определению, изменение магнитного потока через замкнутый контур со скоростью один вебер в секунду наводит в… … Википедия
Информатика. Базовый курс
Кодирование звука и видео информации

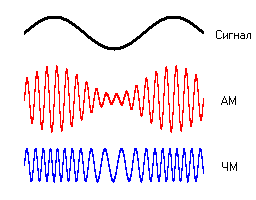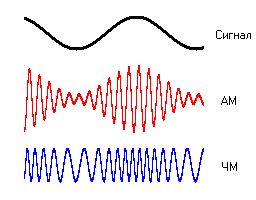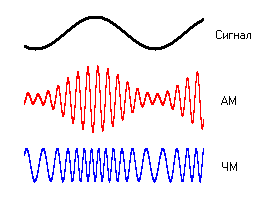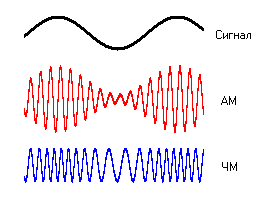
Хранение и передача аналогового звукового сигнала осуществляется за счёт представления его в виде электрического сигнала с помощью модуляции.
Модуляция – процесс изменения одного или нескольких параметров (амплитуды, частоты или фазы) высокочастотного колебания по закону низкочастотного сигнала (несущей частоты).
Существуют разные виды модуляции:
Амплитудная (АМ, amplitude modulation ) – изменение высокочастотных колебаний с частотой, равной частоте звукового сигнала. Например, несущей частотой может быть питание сети – 50 Гц. Или радиоволна СВ (MW) диапазона от 300 кГц до 3 МГц.
Частотная (FM, frequency modulation) – модуляция при которой информационный сигнал управляет несущей частотой. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
Цифровой сигнал
Для того чтобы аналоговый (непрерывный) сигнал представить последовательностью чисел определённой разрядности, его необходимо превратить в дискретный (прерывистый) сигнал, а затем подвергнуть квантованию.

На современном ПК карта всегда интегрирована в материнской плате, и имеет разрядность не ниже 24 бит.
Оцифровка звука – дискретизация и квантование аналогового сигнала.
1-й этап: Дискретизация сигнала по времени
Допустим, Вы, с помощью микрофона записали свой голос длительностью 5 сек. Этот фрагмент можно разбить на равные малые временный отрезки, которые в сумме дают нам 5 сек. Получаем частоту дискретизации (f, Гц), которая является обратной величиной времени: t сек. При частоте дискретизации 8 кГц=8 000 Гц, из формулы получаем отрезок, равный 0,000125 сек. или 125 миллисекунд.
 2-й этап: Квантование сигнала по уровню
2-й этап: Квантование сигнала по уровню
Чем больше уровней будет доступно для кодирования временных отрезков, тем ближе к аналогу будет закодированный файл, но при этом объём файла увеличится.
Например, возьмём 8 уровней, чтобы их закодировать в двоичный код нам достаточно 3 бита, что мы получаем из формулы Хартли:
2³=8 – комбинаций двоичного ряда чисел от 000 до 111.
Параметр (i) – называется глубина кодирования. 8 бит – 256 уровней, 16 бит – 65 536 уровней, 24 бита – более 16 млн. уровней.
3 этап: Определяем скорость потока звука
Частота дискретизации – 22 кГц, глубина кодирования – 16 бит. Произведение этих двух величин дает нам скорость потока 352 кбит/сек.
Именно такой канал передачи данных потребуется для воспроизведения звукового файла в режиме он-лайн.
Расчёт количество звуковой информации
Для определения информационного объёма звуковой информации, нам необходимы следующие параметры:
Задача 1:
Одна минута записи цифрового аудиофайла занимает 1,3 МБ, разрядность звуковой платы — 8 бит. С какой частотой дискретизации записан звук?
Воспользуемся формулой: I=f∙t∙i∙n , из формулы видно что для нахождения частоты дискретизации формула примет вид: f=I/t∙i∙n.
1,3 МБ = 13,31,2 КБ = 1 363 148,8 Байт. Принимая во внимание что 8 бит = 1 Байту, делим 1 363 148,8 на 60, канал у нас записан 1, поэтому n=1.
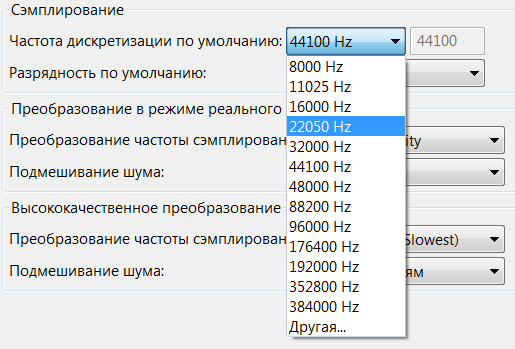
Ответ: 22719,1 Гц или 22 050 Гц, см. основные настройки параметров звукового файла в программе Audacity
Задача 2:
Две минуты записи цифрового аудиофайла занимают на диске 5,1 МБ. Частота дискретизации — 22 050 Гц. Какова разрядность аудиоадаптера?
Решение: 5,1 МБ = 5 347 737,6 Байт, делим по формуле: i = I / f∙ t ∙ n.
5 347 737,6 / 22 050 ∙ 120 = 2,02 Байт.
Ответ: 16 бит.
Кодирование видео
Информация хранится на различных носителях в виде файлов. Файл занимает память и может быть измерен в единицах измерения информации: бит, Байт, КБ и т.д.
Стремительное развитие интернета резко увеличило обмен информацией между людьми, для оптимизации хранения данных люди стали использовать специальные алгоритмы сжатия.
В основе цифрового видео лежит графический и звуковой файлы. Если рассчитать объём видеофайла без сжатия, нам необходимо учитывать тот факт, что человек начинает воспринимать смену кадров (картинок), как непрерывное плавное движение, если за 1 сек. будет мелькать 24 кадра.
Основы ТВ
Для приёма телевизионного сигнала используется антенна и приёмник. Приёмник – это электронная схема, которая преобразует сигнал в изображение на экране. В этом процессе участвует генератор кадровой развёртки и строчной.
Кадровая развёртка формируется на частоте, близкой к частоте переменного тока в бытовых электросетях – 50 Гц.
Кадровая развёртка, в сочетании со строчной служит для преобразования плоского двумерного изображения в одномерную последовательность, то есть, видеосигнал, а в телевизоре или мониторе компьютера для преобразования видеосигнала обратно в изображение на экране.
Для создания такой последовательности, используются специальные стандарты разложения:
576i, 625/50 — стандарт разложения, принятый для аналогового и цифрового телевидения в Европе, России, Австралии, странах Африки и Азии. 576 – это количество активных строк для аналогового телевидения и число пикселей по вертикали, для цифрового. Буква «i», англ. Interlace означает чересстрочную развёртку, передающую 25 целых кадров в 50 полях за 1 секунду.
480i, 525/60 — стандарт разложения, принятый в США, число активных строк составляет 480.
Существует также прогрессивная (p) кадровая развёртка, где все строки каждого кадра отображаются последовательно. Прогрессивная развертка стала широко распространена с появлением персональных компьютеров. Для комфортного чтения мелкого текста с экрана монитора, чересстрочная развертка стала малопригодна, так как мерцание строк вызывало быстрое утомление глаз.
Помимо развёртки существует ещё и соотношение сторон: аналоговое ТВ – 4:3, цифровое ТВ – 16:9, широкоформатное.
Форматы со сжатием
Давайте для начала посчитает объём видеофайла без сжатия, длительность 1 час 30 мин., 576i, 16:9. Звук записан с частотой дискретизации – 44 100 Гц, глубина кодирования 24 бит.
Решение:
Видео: I = 576 ∙ 1024 ∙ 25 ∙ 5400 ∙ 24 = 1 911 029 760 000 бит = 222,5 ГБ
Звук: I = 44 100 ∙ 5400 ∙ 24 = 5 715 360 000 бит = 681,3 МБ = 0,665 ГБ
Ответ: 223,2 ГБ.
Графический формат JPEG
Алгоритм JPEG (от англ. Joint Photographic Experts Group) в большей степени пригоден для реалистичных изображений с плавными переходами яркости и цвета, таковыми являются фотографии.
В основу алгоритма заложен переход от цветового пространства RGB к цветовому пространству YCbCr. Y – компонент яркости, Cb и Cr – синий и красный цветоразностные компоненты. Суть сжатия состоит в том что для каждого блока пикселей 2х2 записывается не 12 значений, а 6, за счёт использования усреднённого компонента цвета.
Видео и аудио форматы MPEG
Алгоритм MPEG (англ. Moving Picture Experts Group) – стандарты сжатия и передачи цифровой видео и аудио информации. Базовым объектом кодирования в стандарте MPEG является кадр телевизионного изображения. Поскольку в большинстве фрагментов фон изображения остается достаточно стабильным, а действие происходит только на переднем плане, сжатие начинается с создания исходного кадра.
При сжатии аудио используются хорошо разработанные психоакустические модели, чтобы выбросить звуки, которые не слышны человеческому уху.
Современные цифровые стандарты
Современные дисплеи и мониторы уже давно вышли за рамки старых добрых стандартов.
Что означает частота сигнала в 70 гц информатика
Реальные сигналы не идеальны, они никогда не бывают строго периодическими. Тем не менее, по отношению к реальным сигналам также используется понятие частоты. Что понимают под частотой в этом случае?
Введение
Понятие частоты периодического сигнала
Рис. %img:pf
* В математике также рассматриваются «почти периодические» функции, но это весьма специфический вопрос и в математике этим термином обозначается не совсем то, что имеется в виду под «почти периодическими» функциями в технике.
Рис. %img:hf
Частота реального сигнала. Мгновенная частота
Строгие определения и формальные теоретические подходы хороши для математики. В реальной жизни, в технике, сигналы никогда не бывают периодическими. Прежде всего, потому что никакой сигнал не может длиться бесконечно долго. Сигнал имеет начало и конец, что уже нарушает идеальную периодичность. Но даже если отвлечься от этого, скорее философского вопроса о конечности существования, то и за время существования сигнала, строгая периодичность недостижима. С другой стороны, некоторая степень регулярности и повторяемости характерна для очень многих реальных сигналов.
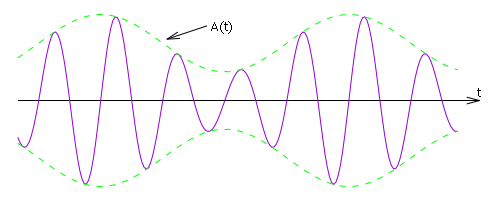
Рис. %img:cf
Заметим, что даже в случае периодических с математической точки зрения, идеальных сигналов, иногда бывает удобнее рассматривать их как «не вполне» периодические, с изменяющейся во времени амплитудой и/или частотой.
Очевидно, что период \( T = 2 \pi / \omega \) несущего колебания уже не является периодом модулированного сигнала из-за множителя \( (1 + m \sin \Omega t) \), который изменится через время T.
Излишне говорить, что с практической точки зрения такой подход совершенно неудобен; истинные частота и период рассмотренного сигнала абсолютно не отражают его реальных свойств. В то же время, мгновенная частота, которая в случае амплитудно-модулированного сигнала равна частоте несущего сигнала \( \omega \), оказывается намного более объективной и информативной характеристикой сигнала.
Очень точному измерению поддаётся среднее значение частоты сигнала, об этом далее.
Среднее значение частоты. Измерение частоты
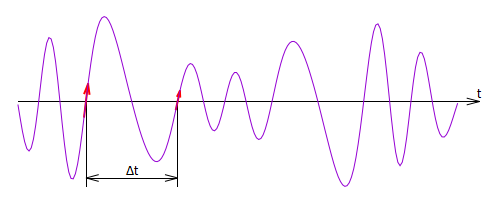
Рис. %img:mf
Получили что для того, чтобы измерить среднее значение частоты, достаточно измерить промежуток времени между двумя моментами, когда сигнал проходит через нулевое значение (в одном направлении). Впрочем, этот результат вполне соответствует интуитивному представлению о периоде реального сигнала и соотношению между периодом и частотой.
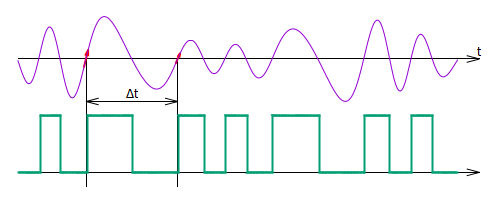
Рис. %img:df
На самом деле, обязательно наличие гистерезиса при преобразовании (порог переключения от 0 к 1 должен быть выше, чем порог обратного переключения). В противном случае, вблизи порога переключения будем получать пачки паразитных импульсов из-за наличия шумов и помех в сигнале. Но это детали реализации, не изменяющие самого принципа.
Динамическая погрешность измерений
Мы нашли способ определения средней частоты сигнала за некоторый интервал времени с высокой точностью. Но если частота сигнала изменяется, средняя частота даёт слишком мало информации о сигнале. Зачастую бывает необходимо знать, как во времени изменяется мгновенная частота сигнала и насколько сильно она отклоняется от среднего значения.
Заметим, что если частота изменяется не по гармоническому закону, всё равно, мгновенную частоту как функцию можно разложить на гармонические составляющие и рассматривать воздействие операции усреднения на каждую составляющую по отдельности. Это возможно, поскольку операция усреднения является линейной.
На основе полученных выводов можем должным образом выбрать интервал измерения.
Если идёт речь о достижении как можно более высокой точности в измерении мгновенной частоты, то следует далее уменьшать интервал измерения. С уменьшением интервала, результат всё более приближается к мгновенной частоте, т.е. уменьшается динамическая погрешность измерения, но одновременно с этим растёт погрешность метода. Это ограничивает предельную точность измерения частоты путём измерения средней частоты сигнала. Не имеет смысла снижать абсолютную динамическую погрешность \( <\Delta>_2 \) до значений меньше абсолютной погрешности метода \( \Delta_1 \).
Пример. Сигнал имеет среднюю частоту f0 = 100 кГц, мгновенная частота отклоняется от среднего значения на величину \( \Delta f = 1 \text < Гц>\), причём отклонение описывается синусоидой с частотой F = 10 Гц. Требуется определить оптимальный интервал измерения (при котором погрешность метода достигает динамической погрешности измерения), если частота опорного генератора составляет fr = 24 МГц. Вычисления по приведённой выше формуле дают результат \( \Delta t \approx 0.03\text < с>\) (абсолютная погрешность метода измерения и динамическая погрешность при этом оказываются порядка 0.14 Гц).
Другим простым, но представляющим интерес примером, является измерение средней частоты сигнала, мгновенная частота которого на некотором интервале изменяется линейно. Легко показать (настолько легко, что подробно не будем на этом останавливаться), что результат будет равен мгновенной частоте в момент, соответствующий середине интервала измерения, или, что то же самое, среднему арифметическому мгновенных частот на концах интервала измерения.
Литература
Особенно хотелось бы отметить книгу «Сигналы, помехи, ошибки. «. Это замечательная книга, в которой хорошо раскрывается понятие мгновенной частоты; поясняется, в каких случаях уместно говорить о частоте сигнала, а когда следует переходить к рассмотрению спектра, а также подробно обсуждаются многие другие вопросы. Материал излагается довольно живо, доступно, но не упрощённо. И что приятно, книга не лишена тонкого ненавязчивого юмора.
В математических энциклопедиях можно найти определения базовых понятий (периодическая функция; почти периодическая функция; период; частота).
В энциклопедии по физике также можно найти аналогичные определения периодичности, периода, частоты и т.д.



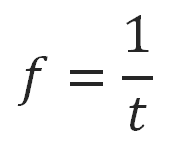 2-й этап: Квантование сигнала по уровню
2-й этап: Квантование сигнала по уровню