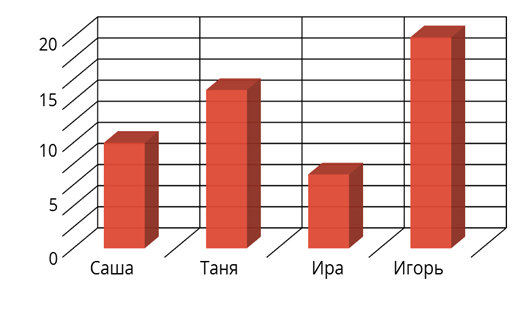Что относится к графическим моделям

Графические информационные модели

Вы будете перенаправлены на Автор24

Свойства графических информационных моделей

Графическая информационная модель – способ представления описываемых объектов и процессов в виде изображений. С помощью таких моделей передаются внешние признаки – форма, размер, цвет.

Поскольку человек с помощью зрения получает большую часть информации (порядка 70%), то по эффективности восприятия рисунок зачастую оказывается более эффективным, чем текст, формулы или устный рассказ.

Графические информационные модели, видимо, появились в человеческой практике раньше других. Рисунки, отображающие план местности и места охоты, археологи находят на стенах пещер, где обитали доисторические люди.

Типы графических моделей

Примеры графических моделей:

Рисунок 1. Чертеж. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Способы исполнения карт, схем, чертежей регламентированы отраслевыми стандартами. Так, географические карты выполняются в заданном масштабе, с использованием определенных правил преобразования трехмерной поверхности в двухмерную (проекции), с нанесением сетки координат, с использованием определенных цветов для обозначения высот и глубин. Кроме того, географические карты изображаются по-разному в зависимости от назначения: физические, экономические, климатические, демографические, военные и т.д.

Схемы также различаются в зависимости от отрасли. Существуют стандарты для черчения электронных схем, схем монтажа оборудования (например, электросилового, водопроводного) и т.п.

Существуют менее регламентированные формы графических моделей, такие, как эскизы. Они применяются там, где требуется быстро зафиксировать конструкторскую мысль, передать ее исполнителю. Нет строгих правил при формировании графиков и диаграмм. Однако и при рисовании произвольных графических моделей принято придерживаться определенных правил и рекомендаций.

Рисунок 2. Рекомендации по отображению диаграммы. Автор24 — интернет-биржа студенческих работ

В приведенном примере нужно расположить информацию на осях таким образом, чтобы данные легко считывались. Если нанести информацию об уровне образования на горизонтальную ось, большое количество текста помешает восприятию. Кроме того, придется задействовать большое количество цветов и штриховок. Но при упрощении второй оси (умеренные цифры) график легко разворачивается на 90 градусов, дополнительная фактура становится ненужной.

Графические модели и вычислительная техника

Современное программное обеспечение предоставляет широкие возможности для подготовки графических моделей. Приведем несколько примеров таких приложений:

Особо следует отметить то обстоятельство, что графические модели используются и при разработке самого программного обеспечения: с помощью диаграмм семейства UML проектируются компьютерные программы. Такие диаграммы не зависят от предметной области и могут применяться в любом программном проекте. Кроме того, для подготовки таких диаграмм не нужна компьютерная техника (хотя ее применение и возможно). Диаграммы и схемы рисуются фломастерами на пластиковых досках или ватмане в ходе «мозговых штурмов», к которым могут быть привлечены как непосредственные разработчики, так и представители заказчика.

Рисунок 3. Диаграмма случаев использования из семейства UML. Автор24 — интернет-биржа студенческих работ

Проектирование с помощью UML начинается от определения случаев использования (Use Case). Дальнейшие уточнения могут идти многими способами, но конечной целью процесса проектирования является формирование диаграмм классов. На их основе с помощью специального программного обеспечения может быть даже частично сформирован компьютерный код, который программистам останется только конкретизировать и отладить.

Источник

Графические информационные модели. Многообразие графических информационных моделей

Урок 5. Информатика 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Графические информационные модели. Многообразие графических информационных моделей»

Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. Графические информационные модели являются простейшим видом моделей. С их помощью передаются внешние признаки объекта – размер, форма, цвет. Графические модели несут в себе больше информации, чем словесные.

Для более наглядного и понятного представления информации в графических информационных моделях используются графические изображения (образные элементы), которые могут быть дополнены текстами, числами и символами. Примерами графических информационных моделей являются схемы, карты, чертежи, графики, диаграммы и много другое.

Разберёмся более подробно с каждой из них.

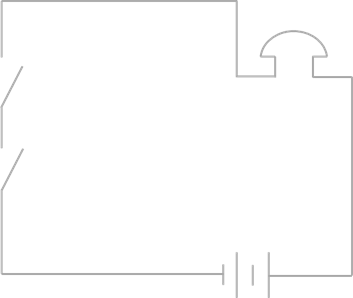
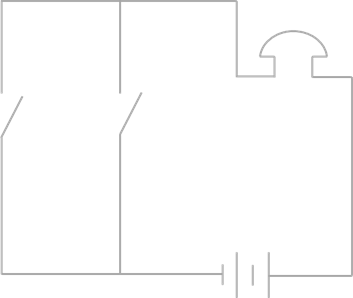
Cхема – это графическое отображение состава и структуры сложной системы. Можно обратиться к ранее рассматриваемому примеру: две электрические схемы соединения переключателей.

Схема последовательного соединения переключателей

Схема параллельного соединения переключателей

На первой представлено последовательное соединение, а на второй – параллельное. Можно заметить, что с помощью схемы легче разбираться с такими задачами, нежели использовать словесное описание. Схемы используются на уроках биологии, истории и так далее.

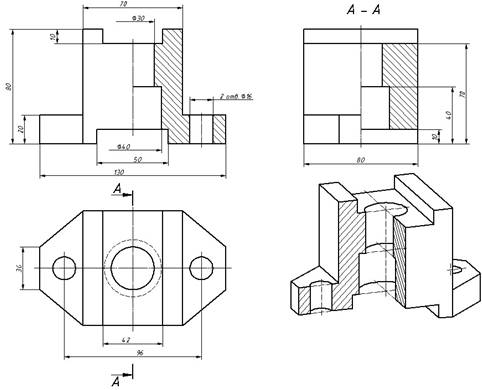
Следующая графическая информационная модель – чертеж. Чертеж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования. При построении чертежа используются изображения, числа, текст. С помощью изображений мы получаем представление о форме объекта, с помощью чисел – о размере, с помощью текста – о названии объектов, размерах, в которых выполнены изображения. Примером чертежа является изображение детали перед её изготовлением.

На чертеже изображена деталь в разрезе, чтобы лучше было видно все части, составляющие нашу деталь, присутствуют размеры (числа).

Рассмотрим такую графическую информационную модель как карта. Карта используется для отображения местности в уменьшенном масштабе, которая является для нее объектом моделирования. Например, с помощью карты мы можем узнать сколько километров от Москвы до Санкт-Петербурга, как добраться на метро или автобусе с одного остановочного пункта до другого, где находится Будапешт и много другое. Для различных целей используются разнообразные карты: политическая, географическая, тематическая и другие.

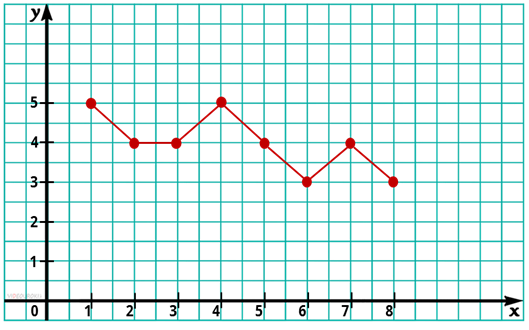
Перейдем к графикам. График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

Расставим точки в соответствии с данными на координатной плоскости и соединим их линиями.

Мы получили необходимый график, с помощью которого можно сделать вывод, что знания Максима по математике ухудшились. Ещё одним примером графика является кардиограмма сердца. Кардиограмма точно определяет в каком ритме бьётся сердце.

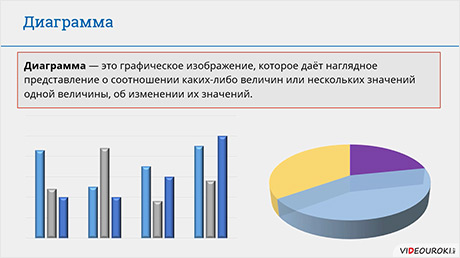
Перейдём к диаграммам. Диаграмма – это графическое изображение, которое даёт наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Диаграммы бывают нескольких видов, но более подробно мы с ними познакомимся при изучении электронных таблиц.

А сейчас рассмотрим несколько примеров.

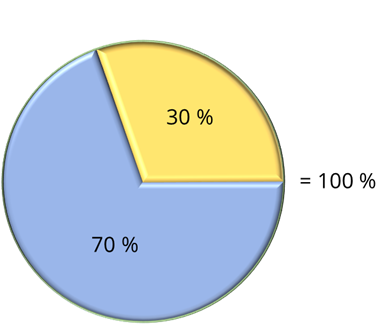
Первый: Наша планета состоит из воды и суши. Вода составляет семьдесят процентов от планеты, а суша – тридцать. Изобразим всё это с помощью круговой диаграммы. Нарисуем круг. Он будет изображать планету и соответственно будет равен ста процентам. Затем изобразим семьдесят процентов суши и тридцать процентов воды.

На данной диаграмме мы можем увидеть соотношение воды и суши.

Теперь рассмотрим ещё один пример. Саша тратит на дорогу от дома до школы 10 минут, Таня – 15 минут, Ира – 7 минут и Игорь – 20 минут. Давайте все это изобразим с помощью диаграммы. На оси X напишем имена учащихся, а на оси Y – время, затраченное на дорогу. Затем каждому учащемуся нарисуем столбик по высоте соответствующий времени его пути.

Таким образом мы получили столбчатую диаграмму.

· Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений.

· Схема – это графическое отображение состава и структуры сложной системы.

· Чертёж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования.

· График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.

· Диаграмма – это графическое изображение, которое дает наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений.

Источник

Урок 4
§1.3 Графические информационные модели

Ключевые слова:

• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево

1.3.1. Многообразие графических информационных моделей

В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.

Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта. Примеры схем приведены на рис. 1.5.

Рис. 1.5. Примеры схем, используемых на уроках физики, биологии, истории

Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.

Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.

График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.

Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.

1.3.2. Графы

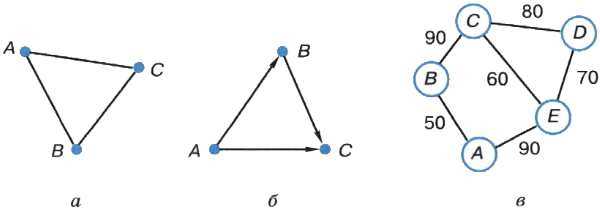
Если некоторые объекты изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой; при этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной.

Граф называется неориентированным, если его вершины соединены рёбрами (рис. 1.6, а). Вершины ориентированного графа соединены дугами (рис. 1.6, б). Путь — это последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую.

Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. На рис. 1.6, в с помощью взвешенного неориентированного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.

Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.

Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.

Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.

Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.

Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс1* высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.

Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.

Ресурс «Живая Родословная» (145555) — инструмент для формирования и анализа генеалогических деревьев, содержащий примеры родословных. С его помощью вы можете изучить генеалогические деревья многих известных семей и построить генеалогическое дерево своей семьи (http://sc.edu.ru/).

Класс — множество объектов, обладающих общими признаками.

1.3.3. Использование графов при решении задач

Графы удобно использовать при решении некоторых классов задач.

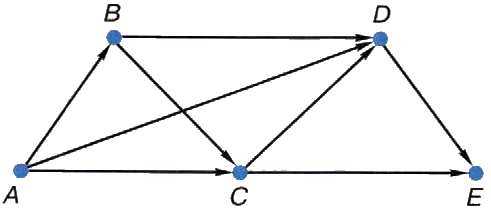
Пример 1. На рисунке 1.7 изображена схема дорог, связывающих торговые точки А, В, С, D, Е. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки Е?

Рис. 1.7. Схема дорог, представленная ориентированным графом

В вершину Е можно попасть только из вершин С и D. Если мы будем знать число путей из вершины А в вершину С и из вершины А в вершину D, то, сложив их, получим искомое число путей из А в Е. Действительно, для того чтобы попасть из вершины А в вершину Е, мы просто все пути из вершины А в вершину С дополним дугой СЕ, а пути из вершины А в вершину D дополним дугой DE. Число путей при этом не изменится. Итак, число путей из вершины А в вершину Е равно сумме путей из А в С и из А в П.

Можно сказать, что наша задача распалась на две более простые задачи. Решим каждую из них в отдельности.

В вершину С можно попасть непосредственно из вершины А и из вершины В. В свою очередь, существует единственный путь из вершины А в вершину В. Таким образом, из вершины А в вершину С можно попасть двумя путями: 1 (напрямую из А) + 1 (через В) = 2.

Попробуйте доказать, что путь из вершины А в вершину В — единственный.

Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин А, В и С:

1 (напрямую из А) + 1 (через В) + 2 (через С) = 4.

Итак, существуют четыре пути из вершины А в вершину D.

Теперь выполним подсчёт путей из А в Е:

2 (через С) + 4 (через D) = 6.

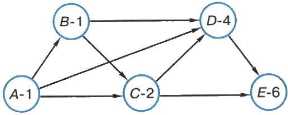
Решение задачи будет гораздо проще, если двигаться от вершины А (начало маршрута) к вершине Е и проставлять веса вершин — число путей из А в текущую вершину (рис. 1.8). При этом вес вершины А можно принять за 1. Действительно, существует единственный способ попасть из А в А — оставаться на месте.

Рис. 1.8. Схема дорог, представленная взвешенным ориентированным графом

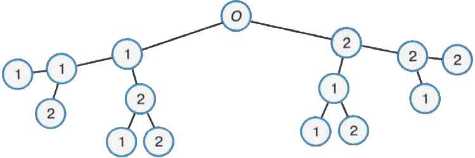
Пример 2. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.9.

Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.

Рис. 1.9. Дерево для решения задачи о записи трёхзначных чисел

В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. (Вспомните правило умножения из комбинаторики!)

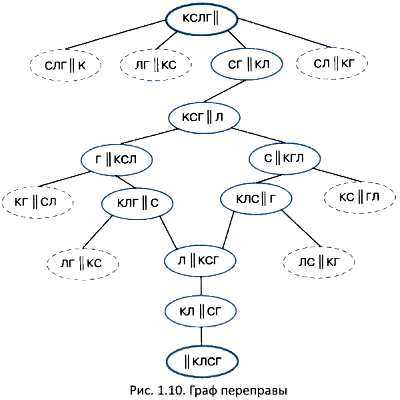
Пример 3. Рассмотрим несколько видоизменённую классическую задачу о переправе.

На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?

Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.10).

Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.

На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:

1) крестьянин перевозит лису;
2) крестьянин возвращается;
3) крестьянин перевозит собаку;
4) крестьянин возвращается с лисой;
5) крестьянин перевозит гуся;
6) крестьянин возвращается;
7) крестьянин перевозит лису.

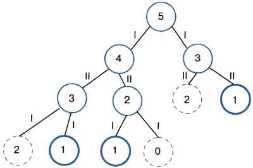
Пример 4. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.

Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).

Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.

Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.

На рис. 1.11 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.

САМОЕ ГЛАВНОЕ

В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы.

Граф состоит из вершин, связанных линиями — рёбрами или дугами. Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весами вершин (рёбер, дуг).

Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?

2. Какие информационные модели относят к графическим?

3. Приведите примеры графических информационных моделей, с которыми вы имеете дело:

а) при изучении других предметов;
б) в повседневной жизни.

4. Что такое граф? Что является вершинами и рёбрами графа на рис. 1.6, в? Приведите примеры цепей и циклов, имеющихся в этом графе. Определите, какие два пункта наиболее удалены друг от друга (два пункта считаются самыми удалёнными, если длина кратчайшего пути между ними больше, чем длина кратчайшего пути между любыми другими двумя пунктами). Укажите длину кратчайшего пути между этими пунктами.

5. Приведите пример системы, модель которой можно представить в форме графа. Изобразите соответствующий граф.

6. Грунтовая дорога проходит последовательно через населённые пункты А, В, С и D. При этом длина грунтовой дороги между А и В равна 40 км, между В и С — 25 км, и между С и D — 10 км. Между А и D дороги нет. Между А и С построили новое асфальтовое шоссе длиной 30 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.

7. На рисунке изображена схема дорог, связывающих торговые точки А, Б, В, Г, Д, Б, К. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки К?

8. Работая в группе, составьте семантическую сеть по одной из русских народных сказок: «Колобок», «Курочка Ряба», «Репка».

9. Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы.

10. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8 при условии, что в записи числа не должно быть одинаковых цифр?

11. Сколько существует трёхзначных чисел, все цифры которых различны?

12. Для составления цепочек используются бусины, помеченные буквами А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?

13. Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Электронное приложение к уроку

Файлы	Материалы урока	Ресурсы ЭОР

Cкачать материалы урока

Источник