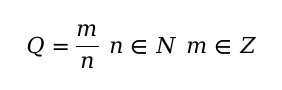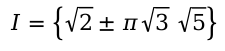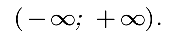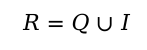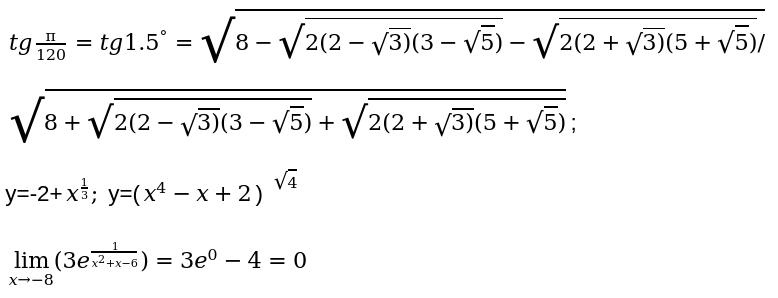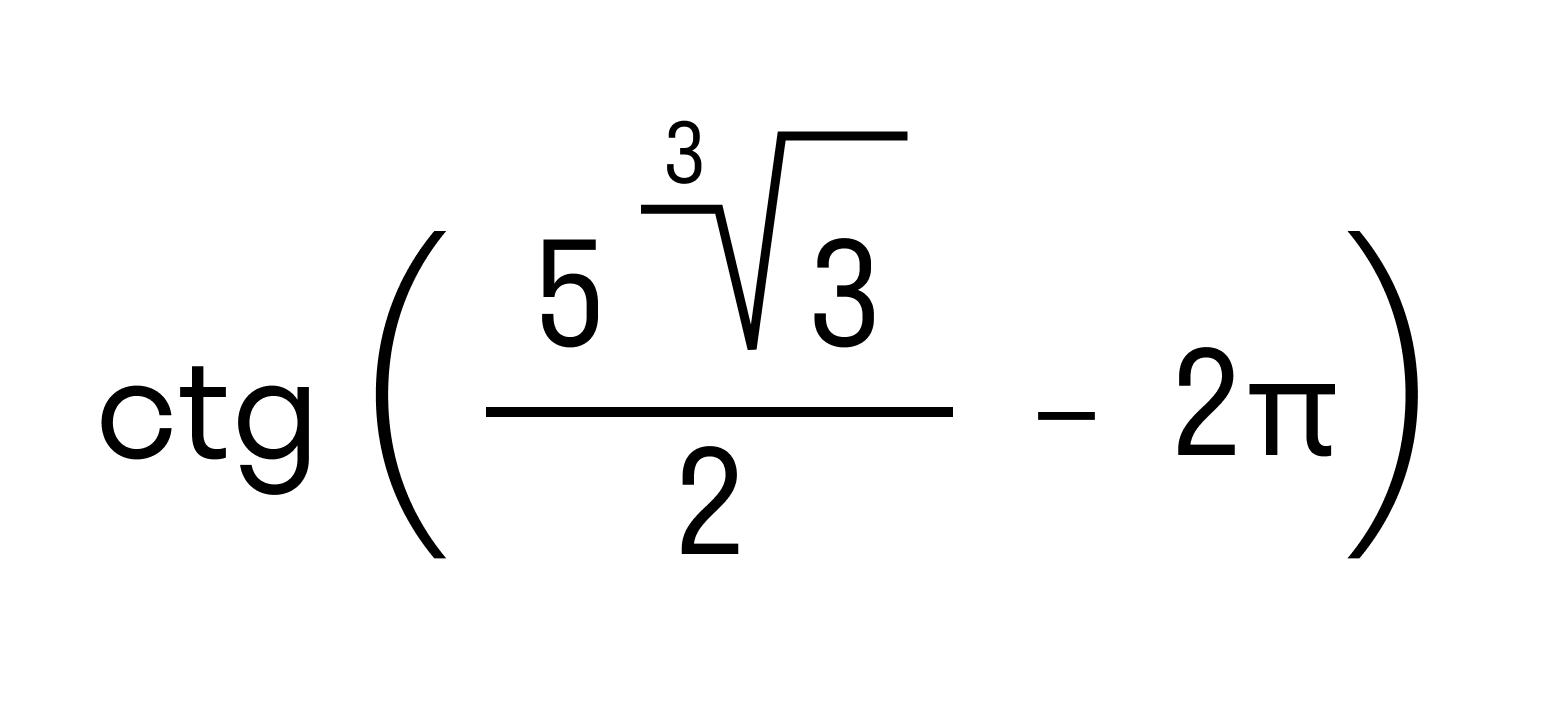Что относится к действительным числам

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

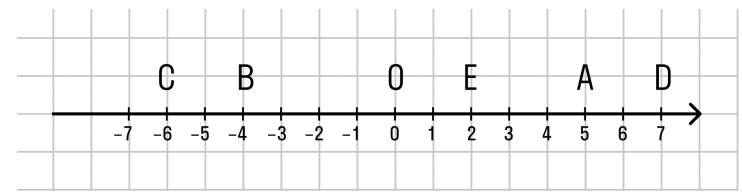
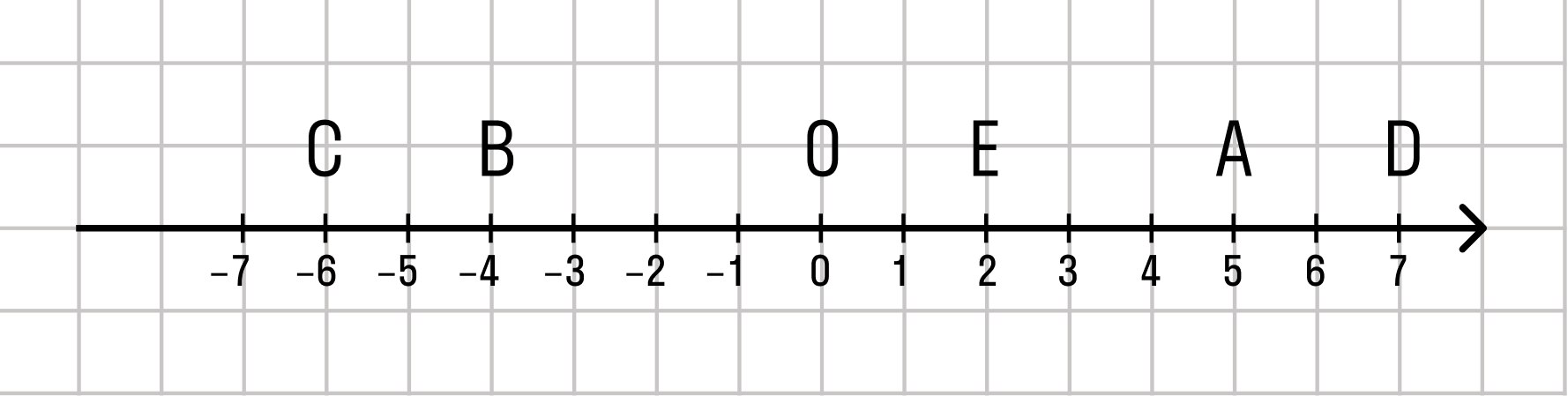
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Действительные числа

Время чтения: 12 минут

Понятие действительного числа

Через R обычно выражается множество значений действительных чисел.

Рациональные числовые значения. Эту категорию чисел можно выразить, как положительное или отрицательное дробное значение. Еще есть вариант представлять рациональное число в виде нулевого значения.

Множество рациональных данных имеет следующий вид:

Иррациональное число. Данные значения невозможно выразить как деление двух и более целых данных. Такие числа представлены и выражаются как бесконечная, не имеющая определенного периода десятичная дробь.

Множество иррациональных чисел.

Данное множество, как правило, состоит из определенного множества рациональных чисел. А также, вместе с иррациональными значениями. Характеризуется множество R как область действительных чисел и обозначается

Иначе, можно составить и записать множество двух значений действительных чисел: рационального и иррационального.

Следовательно, любое рациональное число возможно записать в виде окончательной десятичной дроби или бесконечной периодической дроби. Иррациональные значения можно выразить бесконечными не имеющими определенного периода десятичными дробями. Учитывая все вышеизложенное определение действительных чисел можно составить и записать иначе.

Действительные числа — это значения чисел, которые выражаются, как конечная или бесконечная, имеющая вид периодической и непериодической десятичной дроби. Иными словами, их можно назвать, как вещественные.

Примеры действительных чисел

Действительные числа, могут быть и положительные, и отрицательные. Ноль, также будет являться действительным, потому что относится к категории рациональных значений, однако не будут иметь ни положительного ни отрицательного значения.

Используя действительные числа, можно выразить величины, числовые значения, которых изменяются непрерывно. Иначе говоря, действительные числа предоставляют возможность выражать числовые значение непрерывно, которые изменяя величины, через единичное значение.

Действительные числа на координатной прямой

Координатная прямая — это прямая, на которой отображается заданная определенная точка отсчета. Начало берется за нулевое значение и единичный отрезок и заданное направление движения отсчета. Каждую точку прямой всегда выражают действительные значения чисел. Для каждой точки на координатной прямой соответствует действительное числовое значение, иными словами их называют координатные значения точек. Из этого следует, что между действительными и координатными значениями, всегда существует однозначная и определенная взаимосвязь и соответствие.

Нет времени решать самому?

Наши эксперты помогут!

Класс и характеристика действительных чисел

Все действительные значения чисел можно представить по следующей классификации:

Целым вполне возможно назвать, любое число натурального значения. Однако, целое число не всегда будет является натуральным числом, и это следует всегда помнить.

Натуральные числа, можно определить двумя методами:

значения, которые возникают, при подсчете определенных предметов, которые являются числительными (первый день, четвертый урок, третий ребенок);

обозначение конкретных событий или простых предметов (три слова, пять рулонов).

В первом случае нумерация начинается с единичного значения, а для второго характерен подсчет, с нулевого знака.

Сравнивая с нулевым значением, можно сформулировать и другие определения, конкретно опираясь на ноль.

Например: числа, которые являются меньше нуля, можно назвать отрицательными целыми числовыми значениями.

Дадим определения таким значениям неотрицательные и не положительные.

Как мы уже говорили ранее числовое данное равное нулю, не относится ни к какому из изученных натуральных значений. Простыми примерами неотрицательных чисел могут быть следующие значения: 45; 142; 26589;105689.

Выразить действительные числа, можно в следующем виде:

Применяя все перечисленные свойства числа действительного типа, можно составлять различного вида математические примеры, уравнения, тригонометрические и алгебраические функции. Составим и запишем несколько примеров решения:

Принцип сравнения действительных чисел

Большим будет считаться, то значение которое располагается правее относительно координатной прямой.

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Действительные числа, определение, примеры.

В данной статье собраны основные сведения про действительные числа. Сначала дано определение действительных чисел и приведем примеры. Дальше показано положение действительных чисел на координатной прямой. А в заключение разобрано, как действительные числа задаются в виде числовых выражений.

Навигация по странице.

Определение и примеры действительных чисел

Подобно тому, как рациональные числа объединяют целые числа и дробные числа, действительные числа объединяют рациональные и иррациональные числа. Отсюда вытекает определение действительных чисел.

Действительные числа – это рациональные и иррациональные числа.

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то озвученное определение действительных чисел можно переформулировать следующим образом.

Действительные числа – это числа, которые могут быть записаны в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.

Из определения действительных чисел следует, что существуют как положительные, так и отрицательные действительные числа, а нуль – ни положительное, ни отрицательное действительное число.

Действительные числа позволяют описывать величины, значения которых могут изменяться непрерывно, чего не позволяют делать рациональные и иррациональные числа по отдельности. Другими словами, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное (эталонное) значение этой величины.

В заключение этого пункта заметим, что действительные числа также называют вещественными.

Действительные числа на координатной прямой

Действительные числа заполняют каждую точку координатной прямой. Каждой точке координатной прямой соответствует единственное действительное число – координата этой точки, а каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Действительные числа в виде выражений

А если пойти дальше, то из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций и т.п. можно составлять всевозможные числовые выражения, значения которых также будут действительными числами. Например, значения выражений и есть действительные числа.

В заключение этой статьи заметим, что следующим этапом расширения понятия числа является переход от действительных чисел к комплексным числам.

Источник

Числа. Действительные числа.

Вещественное, или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.

Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых иррациональные числа.

Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой. Вещественные числа состоят из простых объектов: целых и рациональных чисел.

Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.

Бесконечная десятичная дробь, это десятичная дробь, у которой после запятой есть бесконечное число цифр.

Числа, которые нельзя представить в виде , являются иррациональными числами.

Пример:

Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.

Рациональные и иррациональные числа создают множество действительных чисел. Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая.

Для числовых множеств используются обозначения:

Теория бесконечных десятичных дробей.

Вещественное число определяется как бесконечная десятичная дробь, т.е.:

где ± есть один из символов + или −, знак числа,

a₀ — целое положительное число,

a₁,a₂,…a_n,… — последовательность десятичных знаков, т.е. элементов числового множества <0,1,…9>.

Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:

Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно. Например, предположим даны 2 положительны числа:

Если a₀0, то α b₀ то α>β. Когда a₀=b₀ переходим к сравнению следующего разряда. И т.д. Когда α≠β, значит после конечного количества шагов встретится первый разряд n, такой что a_n≠b_n. Если a_nn, то α b_n то α>β.

Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например, суммой вещественных чисел α и β является вещественное число α+β, которое удовлетворяет таким условиям:

Аналогично определяет операция умножения бесконечных десятичных дробей.

Источник