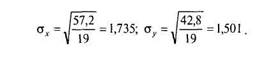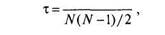Что определяет коэффициент корреляции
Расчет коэффициента корреляции
Методы расчета коэффициента корреляции
Размещено на www.rnz.ru
В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:
Шкала Чеддока количественной оценки степени тесноты связи
| Величина показателя тесноты связи | Характер связи |
|---|---|
| До |±0,3| | Практически отсутствует |
| |±0,3|-|±0,5| | Слабая |
| |±0,5|-|±0,7| | Умеренная |
| |±0,7|-|±1,0| | Сильная |
При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.
Формула расчета коэффициента корреляции
В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента. Общая формула для расчета коэффициента корреляции имеет следующий вид:

Опираясь на математические свойства средней, общую формулу можно представить следующим образом, получив следующее выражение:
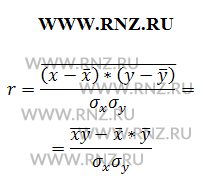
Выполняя дальнейшие преобразование, можно получить следующие формулы вычисления коэффициента корреляции Пирсона:
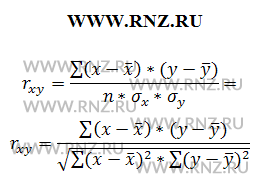
Выполняя вычисление по итоговым данным для расчета показателя корреляции, его можно рассчитать с использованием следующих формул:
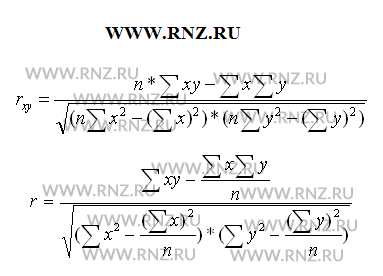
Методом расчета показателя корреляции является вычисление данного показателя с использованием его взаимосвязи с дисперсиями факторного и результативного признаков по следующей формуле:

Также показатель тесноты связи можно определить на основе его взаимосвязи с показателями уравнения регрессии, используя следующее отношение:
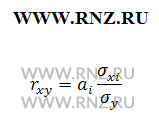
В том случае, когда rxy = 1, то это означает, что все точки (х, у) расположены на прямой и зависимость между х и у относится к функциональным. При указанном условии прямые линии регрессии совпадают. Указанное положение действует также в случае исследования трех и более показателей, если они подчинены закону нормального распределения.
Пример расчета коэффициента корреляции
Приведем пример расчета коэффициента корреляции Пирсона для значений, приведенных в следующей таблице. Для этого используем следующие данные (пример условный):
| Значение показателя X | Значение показателя Y |
|---|---|
| 1,1 | 1,3 |
| 1,9 | 1,1 |
| 1,5 | 1,2 |
| 1,9 | 0,5 |
| 1,9 | 1,5 |
| 1,1 | 1,7 |
| 0,9 | 2 |
| 1 | 0,9 |
| 1,3 | 1,2 |
| 1,5 | 1,7 |
Количество наблюдений менее 30, поэтому в нашем примере для расчета парного коэффициента корреляции используем следующую формулу:
Для этого составим вспомогательную таблицу:
| № п/п | X | Y | xy | x 2 | y 2 |
|---|---|---|---|---|---|
| 1 | 1,1 | 1,3 | 1,43 | 1,21 | 1,69 |
| 2 | 1,9 | 1,1 | 2,09 | 3,61 | 1,21 |
| 3 | 1,5 | 1,2 | 1,8 | 2,25 | 1,44 |
| 4 | 1,9 | 0,5 | 0,95 | 3,61 | 0,25 |
| 5 | 1,9 | 1,5 | 2,85 | 3,61 | 2,25 |
| 6 | 1,1 | 1,7 | 1,87 | 1,21 | 2,89 |
| 7 | 0,9 | 2 | 1,8 | 0,81 | 4 |
| 8 | 1 | 0,9 | 0,9 | 1 | 0,81 |
| 9 | 1,3 | 1,2 | 1,56 | 1,69 | 1,44 |
| 10 | 1,5 | 1,7 | 2,55 | 2,25 | 2,89 |
| Итого | 14,1 | 13,1 | 17,8 | 21,25 | 18,87 |
Полученное значение коэффициента корреляции Пирсона говорит о наличии обратной связи между X и Y. Величина коэффициента корреляции Пирсона показывает, что связь между X и Y слабая.
Онлайн калькулятор расчета коэффициента корреляции
В заключении приводим небольшой онлайн калькулятор расчета коэффициента корреляции онлайн, используя который, Вы можете самостоятельно выполнить расчет значения коэффициента корреляции Пирсона и получить интерпретацию рассчитанного значения. При заполнении формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить расчет коэффициента корреляции онлайн быстро и точно. В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значения показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Онлайн-калькулятор расчета коэффициента корреляции:
Коэффициент корреляции
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Содержание
Коэффициент корреляции
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
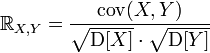
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
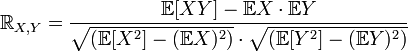
где символ 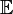
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов ( корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Ограничения корреляционного анализа
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
Полезное
Смотреть что такое «Коэффициент корреляции» в других словарях:
Коэффициент корреляции — Математическое представление о степени связи между двумя сериями измерений. Коэффициент +1 обозначает четкую позитивную корреляцию: высокие показатели по одному параметру (например, рост) точно соотносятся с высокими показателями по другому… … Большая психологическая энциклопедия
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — англ. coefficient, correlation; нем. Korrelationskoeffizient. Мера тесноты связи двух или более переменных. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
коэффициент корреляции — — [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN correlation coefficient … Справочник технического переводчика
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
коэффициент корреляции — 1.33. коэффициент корреляции Отношение ковариации двух случайных величин к произведению их стандартных отклонений: Примечания 1. Эта величина всегда будет принимать значения от минус 1 до плюс 1, включая крайние значения. 2. Если две случайные… … Словарь-справочник терминов нормативно-технической документации
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — (correlation coefficient) мера ассоциации одной переменной с другой. См. Корреляция; Коэффициент корреляции производного значения Пирсона; Коэффициент ранговой корреляции спирмена … Большой толковый социологический словарь
Коэффициент корреляции — CORRELATION COEFFICIENT Показатель степени линейной зависимости между двумя переменными величинами: Коэффициент корреляции может изменяться в пределах от 1 до 1. Если большим значениям одной величины соответствуют большие значения другой (и… … Словарь-справочник по экономике
коэффициент корреляции — koreliacijos koeficientas statusas T sritis automatika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Automatikos terminų žodynas
коэффициент корреляции — koreliacijos koeficientas statusas T sritis fizika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Fizikos terminų žodynas
КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ



В главе 4 мы рассмотрели основные одномерные описательные статистики — меры центральной тенденции и изменчивости, которые применяются для описания одной переменной. В этой главе мы рассмотрим основные коэффициенты корреляции.
Коэффициент корреляции — двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.
История разработки и применения коэффициентов корреляции для исследования взаимосвязей фактически началась одновременно с возникновением измерительного подхода к исследованию индивидуальных различий — в 1870—1880 гг. Пионером в измерении способностей человека, как и автором самого термина «коэффициент корреляции», был Френсис Гальтон, а самые популярные коэффициенты корреляции были разработаны его последователем Карлом Пирсоном. С тех пор изучение взаимосвязей с использованием коэффициентов корреляции является одним из наиболее популярных в психологии занятием.
К настоящему времени разработано великое множество различных коэффициентов корреляции, проблеме измерения взаимосвязи с их помощью посвящены сотни книг. Поэтому, не претендуя на полноту изложения, мы рассмотрим лишь самые важные, действительно незаменимые в исследованиях меры связи — /—Пирсона, r-Спирмена и т-Кендалла’. Их общей особенностью является то, что они отражают взаимосвязь двух признаков, измеренных в количественной шкале — ранговой или метрической.
Вообще говоря, любое эмпирическое исследование сосредоточено на изучении взаимосвязей двух или более переменных.
ПРИМЕРЫ
Приведем два примера исследования влияния демонстрации сцен насилия по ТВ на агрессивность подростков. 1. Изучается взаимосвязь двух переменных, измеренных в количественной (ранговой или метрической) шкале: 1)«время просмотра телепередач с насилием»; 2) «агрессивность».
Читается как тау-Кендалла.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
2. Изучается различие в агрессивности 2-х или более групп подростков, отличающихся длительностью просмотра телепередач с демонстрацией сцен насилия.
Во втором примере изучение различий может быть представлено как исследование взаимосвязи 2-х переменных, одна из которых — номинативная (длительность просмотра телепередач). И для этой ситуации также разработаны свои коэффициенты корреляции.
Любое исследование можно свести к изучению корреляций, благо изобретены самые различные коэффициенты корреляции для практически любой исследовательской ситуации. Но в дальнейшем изложении мы будем различать два класса задач:
исследование корреляций — когда две переменные представлены в числовой шкале;
исследование различий — когда хотя бы одна из двух переменных представлена в номинативной шкале.
Такое деление соответствует и логике построения популярных компьютерных статистических программ, в которых в меню Корреляции предлагаются три коэффициента (/—Пирсона, r-Спирмена и х-Кендалла), а для решения других исследовательских задач предлагаются методы сравнения групп.
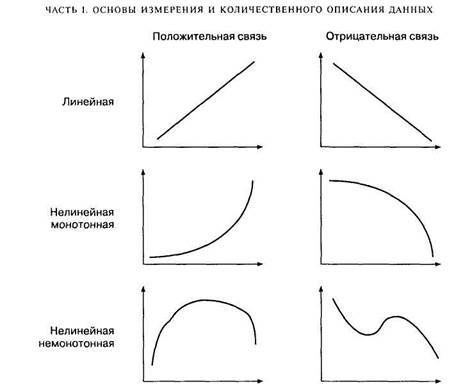
Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий. На рис. 6.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.
Функциональные связи, подобные изображенным на рис. 6.1, являются иде-ализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.
Рис. 6.1. Примеры графиков часто встречающихся функций
В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной — идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых. (Вряд ли на этом основании кому-то придет в голову отрицать факт наличия строгой функциональной связи между длиной и весом тела.)
Итак, в психологии, как и во многих других науках, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания — график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рис. 6.2). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.
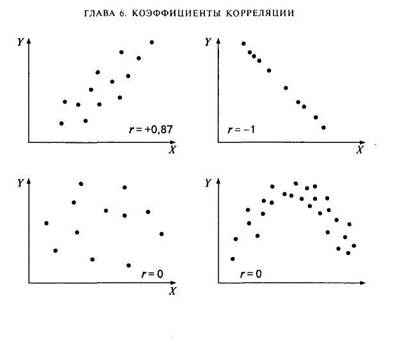 |
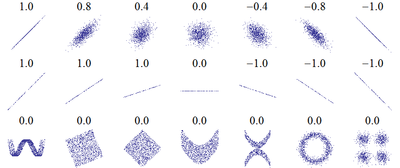
Рис. 6.2. Примеры диаграмм рассеивания и соответствующих коэффициентов корреляции
Коэффициент корреляции — это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от-1 до +1.
Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.
Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ г-ПИРСОНА
r-Пирсона (Pearson r) применяется для изучения взаимосвязи двух метрических переменных, измеренных на одной и той же выборке. Существует множество ситуаций, в которых уместно его применение. Влияет ли интеллект на успеваемость на старших курсах университета? Связан ли размер заработной платы работника с его доброжелательностью к коллегам? Влияет ли настроение школьника на успешность решения сложной арифметической задачи? Для ответа на подобные вопросы исследователь должен измерить два интересующих его показателя у каждого члена выборки. Данные для изучения взаимосвязи затем сводятся в таблицу, как в приведенном ниже примере.
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ.
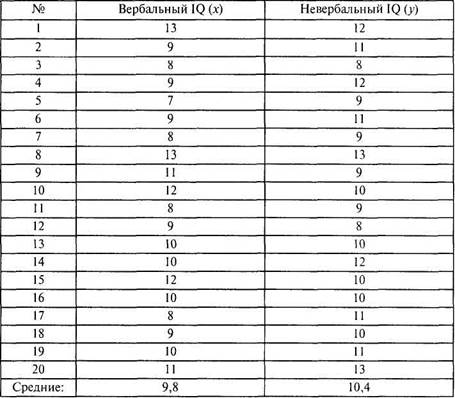
В таблице приведен пример исходных данных измерения двух показателей интеллекта (вербального и невербального) у 20 учащихся 8-го класса.
 |
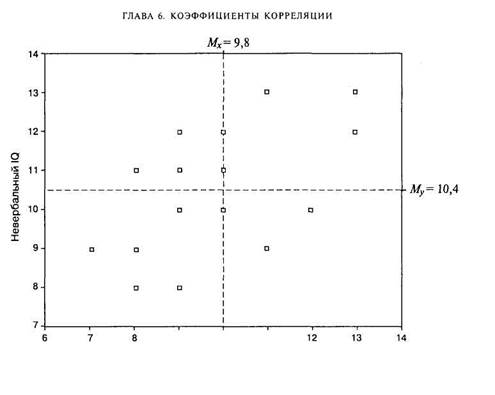
Прежде чем дать формулу коэффициента корреляции, попробуем проследить логику ее возникновения, используя данные примера 6.1. Положение каждой /-точки (испытуемого с номером /) на диаграмме рассеивания относительно остальных точек (рис. 6.3) может быть задано величинами и знаками отклонений соответствующих значений переменных от своих средних величин: (xj — MJ и (у, —Му). Если знаки этих отклонений совпадают, то это свидетельствует в пользу положительной взаимосвязи (большим значениям по х соответствуют большие значения по у или меньшим значениям по х соответствуют меньшие значения по у).Связь между этими переменными можно изобразить при помощи диаграммы рассеивания (см. рис. 6.3). Диаграмма показывает, что существует некоторая взаимосвязь измеренных показателей: чем больше значения вербального интеллекта, тем (преимущественно) больше значения невербального интеллекта.
 |
9 10 11
Рис. 6.3. Диаграмма рассеивания для данных примера 6.1
Для испытуемого № 1 отклонение от среднего по х и по у положительное, а для испытуемого № 3 и то и другое отклонения отрицательные. Следовательно, данные того и другого свидетельствуют о положительной взаимосвязи изучаемых признаков. Напротив, если знаки отклонений от средних по х и по у различаются, то это будет свидетельствовать об отрицательной взаимосвязи между признаками. Так, для испытуемого № 4 отклонение от среднего по х является отрицательным, по у — положительным, а для испытуемого № 9 — наоборот.
Таким образом, если произведение отклонений (х,— Мх) х (у, — Му) положительное, то данные /-испытуемого свидетельствуют о прямой (положительной) взаимосвязи, а если отрицательное — то об обратной (отрицательной) взаимосвязи. Соответственно, если х w у ъ основном связаны прямо пропорционально, то большинство произведений отклонений будет положительным, а если они связаны обратным соотношением, то большинство произведений будет отрицательным. Следовательно, общим показателем для силы и направления взаимосвязи может служить сумма всех произведений отклонений для данной выборки:
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
При прямо пропорциональной связи между переменными эта величина является большой и положительной — для большинства испытуемых отклонения совпадают по знаку (большим значениям одной переменной соответствуют большие значения другой переменной и наоборот). Если же х и у имеют обратную связь, то для большинства испытуемых большим значениям одной переменной будут соответствовать меньшие значения другой переменной, т. е. знаки произведений будут отрицательными, а сумма произведений в целом будет тоже большой по абсолютной величине, но отрицательной по знаку. Если систематической связи между переменными не будет наблюдаться, то положительные слагаемые (произведения отклонений) уравновесятся отрицательными слагаемыми, и сумма всех произведений отклонений будет близка к нулю.
Чтобы сумма произведений не зависела от объема выборки, достаточно ее усреднить. Но мера взаимосвязи нас интересует не как генеральный параметр, а как вычисляемая его оценка — статистика. Поэтому, как и для формулы дисперсии, в этом случае поступим также, делим сумму произведений отклонений не на N, а на TV— 1. Получается мера связи, широко применяемая в физике и технических науках, которая называется ковариацией (Covahance):
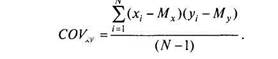 |
13 психологии, в отличие от физики, большинство переменных измеряются в произвольных шкалах, так как психологов интересует не абсолютное значение признака, а взаимное расположение испытуемых в группе. К тому же ковариация весьма чувствительна к масштабу шкалы (дисперсии), в которой измерены признаки. Чтобы сделать меру связи независимой от единиц измерения того и другого признака, достаточно разделить ковариацию на соответствующие стандартные отклонения. Таким образом и была получена формула коэффициента корреляции К. Пирсона:
 |
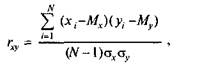
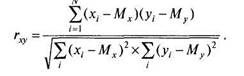 |
Уравнение (6.1) является основной формулой коэффициента корреляции Пирсона. Эта формула вполне осмысленна, но не очень удобна для вычислений «вручную» или на калькуляторе. Поэтому существуют производные формулы — более громоздкие по виду, менее доступные осмыслению, но упрощающие расчеты. Мы не будем их здесь приводить, так как один раз в жизни можно в учебных целях посчитать корреляцию Пирсона и по исходной формуле «вручную», а в дальнейшем для обработки реальных данных все равно придется воспользоваться компьютерными программами.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Для расчета коэффициента корреляции воспользуемся данными примера 6.1 о вербальном и невербальном IQ, измеренном у 20 учащихся 8-го класса. К двум столбцам с исходными данными добавляются еще 5 столбцов для дополнительных расчетов, и внизу — строка сумм.
На первом шаге подсчитываются суммы всех значений одного, затем — другого признака для вычисления соответствующих средних значений Мх и Му: Мх = 9,8; Л/, = 10,4.
Далее для каждого испытуемого вычисляются отклонения от среднего: для Х\\ для Y. Каждое отклонение от среднего возводится в квадрат. В последнем столбике записывается результат перемножения двух отклонений от среднего для каждого испытуемого.
Суммы отклонений от среднего для каждой переменной должны быть равны нулю (с точностью до погрешности вычислений). Сумма квадратов отклонений необходима для вычисления стандартных отклонений по известной формуле (4.7):
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Сумма произведений отклонений дает нам значение числителя, а произведение стандартных отклонений и (./V— 1) — значение знаменателя формулы коэффициента корреляции:
Если значения той и другой переменной были преобразованы в г-значения по формуле:
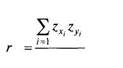 |
то формула коэффициента 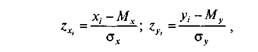
Отметим еще раз: на величину коэффициента корреляции не влияет то, в каких единицах измерения представлены признаки. Следовательно, любые линейные преобразования признаков (умножение на константу, прибавление константы: у; = хр + а) не меняют значения коэффициента корреляции. Исключением является умножение одного из признаков на отрицательную константу: коэффициент корреляции меняет свой знак на противоположный.
На рис. 6.2 приведены примеры диаграмм рассеивания для различных значений коэффициента корреляции. Обратите внимание: на последнем рисунке визуально наблюдается нелинейная взаимосвязь между переменными, однако коэффициент корреляции равен нулю. Таким образом, коэффициент корреляции Пирсона есть мера прямолинейной взаимосвязи; он не чувствителен к криволинейным связям.
КОРРЕЛЯЦИЯ, РЕГРЕССИЯ И КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
Корреляция Пирсона есть мера линейной связи между двумя переменными. Она позволяет определить, насколько пропорциональна изменчивость двух переменных. Если переменные пропорциональны друг другу, то графически связь между ними можно представить в виде прямой линии с положительным (прямая пропорция) или отрицательным (обратная пропорция) наклоном. Кроме того, если известна пропорция между переменными, заданная уравнением графика прямой линии: то по известным значениям переменной ЛГ можно точно предсказать значения переменной Y.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
На практике связь между двумя переменными, если она есть, является вероятностной и графически выглядит как облако рассеивания эллипсоидной формы. Этот эллипсоид, однако, можно представить (аппроксимировать) в виде прямой линии, или линии регрессии. Линия регрессии (Regression Line) — это прямая, построенная методом наименьших квадратов: сумма квадратов расстояний (вычисленных по оси У) от каждой точки графика рассеивания до прямой является минимальной:
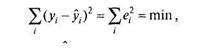 |
 |
 |
где b — коэффициент регрессии (Regression Coefficient), задающий угол наклона прямой; а — свободный член, определяющий точку пересечения прямой оси Y. Если известны средние, стандартные отклонения и корреляция гху, то сумма квадратов ошибок минимальна, если:
 |
Таким образом, если на некоторой выборке измерены две переменные, которые коррелируют друг с другом, то, вычислив коэффициенты регрессии, мы получаем принципиальную возможность предсказания неизвестных значений одной переменной (У— «зависимая переменная») по известным значениям другой переменной (X — «независимая переменная»). Например, предсказываемой «зависимой переменной» может быть успешность обучения, а предиктором, «независимой переменной» — результаты вступительного теста.
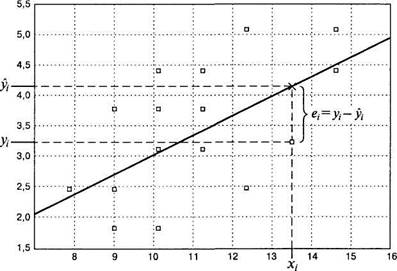
Рис. 6.4. Диаграмма рассеивания и линия регрессии (е,- — ошибка оценки для одного из объектов)
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
С какой степенью точности возможно такое предсказание?
Понятно, что наиболее точным предсказание будет, если \гху\ = 1. Тогда каждому значению Сбудет соответствовать только одно значение У, а все ошибки оценки будут равны 0 (все точки на графике рассеивания будут лежать на прямой регрессии). Если же гху — О, то b = О и у, = Му, т. е. при любом Xоценка переменной Убудет равна ее среднему значению и предсказательная ценность регрессии ничтожна.
Особое значение для оценки точности предсказания имеет дисперсия оценок зависимой переменной. Отметим, что дисперсия оценок равна нулю, если гху = 0 — все оценки равны среднему значению, прямая регрессии параллельна оси X. А если \гху\ = 1, то дисперсия оценок равна истинной дисперсии переменной У, достигая своего максимума:
 |
0 2 раз. Подставляя в формулу выражение для b из (6.2) получаем:
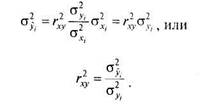 |
Иначе говоря, отношение дисперсии оценок зависимой переменной к ее истинной дисперсии равно квадрату коэффициента корреляции.
Выражение (6.4) дает еще один вариант интерпретации корреляции. Квадрат коэффициента корреляции (R Square) зависимой и независимой переменных представляет долю дисперсии зависимой переменной, обусловленной влиянием независимой переменной, и называется коэффициентом детерминации. Коэффициент детерминации гху, таким образом, показывает, в какой степени изменчивость одной переменной обусловлена (детерминирована) влиянием другой переменной.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Коэффициент детерминации обладает важным преимуществом по сравнению с коэффициентом корреляции. Корреляция не является линейной функцией связи между двумя переменными. Поэтому, в частности, среднее арифметическое коэффициентов корреляции для нескольких выборок не совпадает с корреляцией, вычисленной сразу для всех испытуемых из этих выборок (т. е. коэффициент корреляции не аддитивен). Напротив, коэффициент детерминации отражает связь линейно и поэтому является аддитивным: допускается его усреднение для нескольких выборок.
Дополнительную информацию о силе связи дает значение коэффициента корреляции в квадрате — коэффициент детерминации г 2 : это часть дисперсии одной переменной, которая может быть объяснена влиянием другой переменной. В отличие от коэффициента корреляции г 2 линейно возрастает с увеличением силы связи. На этом основании можно ввести три градации величин корреляции по силе связи:
г 0,7 — сильная связь (50% и более от общей доли дисперсии).
Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей переменной. Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи (корреляции) под влиянием общей причины.
Общей причиной изменчивости двух переменных («третьей переменной») может являться возраст при изучении взаимосвязи различных психологических особенностей в группе детей разного возраста. Предположим, что изучается взаимосвязь между зрелостью моральных суждений — Хп скоростью чтения — К. Но в распоряжении 
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
исследователя имеется лишь выборка из 45 детей разного возраста — от 8 до 14 лет (переменная Z— возраст). Если будет получена существенная положительная корреляция между Хи Y, например гху = 0,54, то о чем это будет свидетельствовать? Осторожный исследователь вряд ли сделает однозначный вывод о том, что зрелость моральных суждений непосредственно связана со скоростью чтения. Скорее всего, дело втом, что и зрелость моральных суждений, и скорость чтения повышаются с возрастом. Иными словами, возраст является причиной согласованной (прямо пропорциональной) изменчивости и зрелости моральных суждений, и скорости чтения.
Для численного определения степени взаимосвязи двух переменных при условии исключения влияния третьей применяют коэффициент частной корреляции
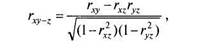 |
где rxy^z — частная корреляция Хи Упри постоянном Z(kiih с учетом Z).
Частная корреляция rxy_z равна гху при любом фиксированном значении Z (в том случае, если Zлинeйнo коррелирует с Хтл У). Например, если значение частной корреляции скорости чтения Хи зрелости моральных суждений К с учетом возраста ZpaBHO 0,2
 |
Один исследователь решил сопоставить антропометрические и психологические данные исследования довольно большой группы детей. Каково же было его изумление, когда обнаружилась существенная положительная корреляция между скоростью решения арифметических задач и размером стопы: гху = 0,42. Оказалось, однако, что дети были разного возраста. Корреляция размера стопы с возрастом составила rxy = QJ, а корреляция скорости решения арифметических задач с возрастом гу, = 0,6. Эти данные позволяют выяснить, взаимосвязаны ли размер стопы и скорость решения арифметических задач с учетом возраста (при условии, что возраст остается неизменным). Для этого необходимо вычислить частный коэффициент корреляции между размером стопы Хи скоростью решения арифметических задач К(при фиксированном возрасте Z):
 |
Таким образом, размер стопы и скорость решения арифметических задач коррелируют исключительно за счет согласованности возрастной изменчивости этих показателей: частная корреляция между ними (с учетом возраста) равна нулю. И если мы возьмем группу детей одного и того же возраста, то корреляция размера стопы и скорости решения арифметических задач будет равна нулю.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Следует быть особенно осторожным, пытаясь дать интерпретацию частной корреляции с позиций причинности. Например, если Zкоррелирует и с 1и с Y, а частная корреляция rxy_z близка к нулю, из этого не обязательно следует, что именно Zявляeтcя общей причиной для Хн Y.
Если обе переменные, между которыми изучается связь, представлены в порядковой шкале, или одна из них — в порядковой, а другая — в метрической, то применяются ранговые коэффициенты корреляции: r-Спирмена или т-Кенделла. И тот, и другой коэффициент требует для своего применения предварительного ранжирования обеих переменных.
Коэффициент корреляции г-Спирмена
Если члены группы численностью /Убыли ранжированы сначала по переменной X, затем — по переменной Y, то корреляцию между переменными Хм Кможно получить, просто вычислив коэффициент r-Пирсона для двух рядов рангов. При условии отсутствия связей в рангах (т. е. отсутствия повторяющихся рангов) по той и другой переменной, формула для r-Пирсона может быть существенно упрощена в вычислительном отношении и преобразована в формулу, известную как г-Спирмена:
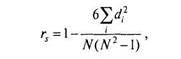 |
где с/, — разность рангов для испытуемого с номером /.
Коэффициент корреляции r-Спирмена (Spearman’s rho) равен коэффициенту корреляции /—Пирсона, вычисленному для двух предварительно ранжированных переменных.
Предположим, для каждого из 12 учащихся одного класса известно время решения тестовой арифметической задачи в секундах (X) и средний балл отметок по математике за последнюю четверть (Y).
| № | X | Y | Ранги X | Ранги Y | d, | d] |
| 4,7 | 2 | |||||
| 4,5 | ||||||
| 4,4 | ||||||
| 3,8 | -4 |
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
| № | X | Y | Ранги X | Ранги У | d, | d] |
| 3,7 | _4 | |||||
| 4,6 | ||||||
| 4,0 | -5 | |||||
| 4,2 | -5 | |||||
| 4,1 | ||||||
| 3,6 | _7 | |||||
| 3,5 | -10 | |||||
| 4,8 | ||||||
| S | — | — |
Для расчета корреляции г-Спирмена сначала необходимо ранжировать учащихся по той и другой переменной. После ранжирования можно проверить его правильность: сумма рангов должна быть равна N(N+ l)/2. Затем для каждого испытуемого надо вычислить разность рангов (сумма разностей рангов должна быть равна 0). После этого для каждого испытуемого вычисляется квадрат разности рангов — результат приведен в последнем столбце таблицы. Сумма квадратов разностей рангов равна 474. Подставляем известные значения в формулу 6.6:
 |
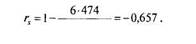 |
Получена умеренная отрицательная связь между успеваемостью по математике и временем решения арифметической задачи.
Отметим: то же значение корреляции было бы получено при использовании формулы r-Пирсона непосредственно к рангам Хи Y. Применяя же формулу г-Пирсо-на к исходным значениям Хи Y, мы получим гху = —0,692.
Коэффициент корреляции т-Кендалла
Альтернативу корреляции Спирмена для рангов представляет корреляция т-Кендалла. В основе корреляции, предложенной М. Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по Xсовпадает по направлению с изменением по У, то это свидетельствует о положительной связи, если не совпадает — то об отрицательной связи.
В примере 6.3 данные испытуемых 1 и 2 свидетельствуют об отрицательной связи — мы видим инверсию: по переменной Ху второго испытуемого ранг больше, а по переменной У— меньше. Данные испытуемых 2 и 3, напротив, демонстрируют совпадение направления изменения переменных.
Корреляция т-Кендалла есть разность относительных частот совпадений и инверсий при переборе всех пар испытуемых в выборке:
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
где Р(р) и P(q) — относительные частоты, соответственно, совпадений и инверсий. Всего в выборке численностью УУ существует N(N— l)/2 всех возможных пар испытуемых. Следовательно,
где Р — число совпадений, Q — число инверсий, а (Р+ Q) = N(N— l)/2. Формулу 6.7 можно представить и в ином виде:
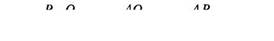 |
т = ^-^- = 1—- I^_ = _Zi—— 1. (6,8)
При подсчете т-Кендалла «вручную» данные сначала упорядочиваются по переменной X. Затем для каждого испытуемого подсчитывается, сколько раз его ранг по доказывается меньше, чем ранг испытуемых, находящихся ниже. Результат записывается в столбец «Совпадения». Сумма всех значений столбца «Совпадения» и есть Р — общее число совпадений, подставляется в формулу 6.8. для вычисления т-Кендалла.
Вычислим т-Кендалла для данных из примера 6.4. Сначала предварительно упорядочиваем испытуемых по переменной X. Затем подсчитываем число совпадений и инверсий для каждого испытуемого, сравнивая по Y его ранг с рангами испытуемых, находящихся под ним. Так, для первого испытуемого ранг по Кравен6,и 6 испытуемых, находящихся ниже него, имеют по Y более высокий ранг: в столбец «Совпадения» записываем 6. Для третьего по счету испытуемого ранг по Y равен 8, трое испытуемых ниже него имеют более высокий ранг, значит, в столбец «Совпадения» записываем 3, и т. д.
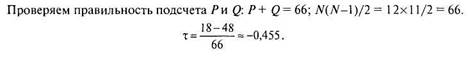 |
| № | Ранги X | Ранги Y | Совпадения | Инверсии |
| Р= 18 | 0 = 48 |
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Для более полной интерпретации полезны соотношения между величиной х-Кендалла и вероятностью отдельно совпадений и инверсий:
 |
Так, т = 0,5 значит, что вероятность совпадений равна 0,75, а вероятность инверсий — 0,25, то есть при сравнении объектов друг с другом прямо пропорциональное соотношение (например, роста и веса) встречается в 3 раза чаще, чем обратно пропорциональное соотношение. Такая интерпретация кажется более понятной, чем, например, интерпретация корреляции Пирсона г= 0,5: «25% изменчивости в весе могут быть объяснены различиями в росте».
т-Кендалла кажется более простым в вычислительном отношении. Однако при возрастании численности выборки, в отличие от л-Спирмена, объем вычислений х-Кендалла возрастает не пропорционально, а в геометрической прогрессии. Так, при N=12 необходимо перебрать 66 пар испытуемых, а при N = 48 — уже 1128 пар, т. е. объем вычислений вбзрастает более, чем в 17 раз.
Отметим важную особенность ранговых коэффициентов корреляции. Для метрической корреляции r-Пирсона значениям +1 или —1 соответствует прямая или обратная пропорция между переменными, что графически представляет собой прямую линию. Максимальным по модулю ранговым корреляциям (+1, —1) вовсе не обязательно соответствуют строгие прямо или обратно пропорциональные связи между исходными переменными Хи Y: достаточна лишь монотонная функциональная связь между ними. Иными словами, ранговые корреляции достигают своего максимального по модулю значения, если большему значению одной переменной всегда соответствует большее значение другой переменной (+1) или большему значению одной переменной всегда соответствует меньшее значение другой переменной и наоборот (—1).
Проблема связанных (одинаковых) рангов
В измерениях часто встречаются одинаковые значения. При их ранжировании возникает проблема связанных рангов (Tied Ranks). В этом случае действует особое правило ранжирования: объектам с одинаковыми значениями
 |
приписывается один и тот же, средний ранг. Например, когда эксперт не может установить различие между двумя лучшими образцами товара, им приписывается одинаковый ранг: (1 + 2)/2 = 1,5. Это сохраняет неизменной сумму рангов для выборки объемом N: N(N + l)/2.
ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
При наличии одинаковых (связанных) рангов формулы ранговой корреляции Спирмена (6.6) и Кендама (6.7и 6.8) не подходят. Хотя сумма рангов и не меняется, но изменчивость данных становится меньше. Соответственно, уменьшается возможность оценить степень связи между измеренными свойствами. При использовании корреляции Спирмена в случае связанных рангов возможны два подхода:
При использовании корреляции х-Кендалла в случае наличия связанных рангов в формулу вносятся поправки, и тогда получается общая формула для вычисления т. коэффициента корреляции хь-Кендалла (Kendall’s tau-b) независимо от наличия или отсутствия связей в рангах:
 |
где х = (1/2)У/?(/?-1) (‘ — количество групп связей по X,ft — численность каждой группы); х = (1/2)У/(/)-1) (/ — количество групп связей по У,/ — численность каждой группы).