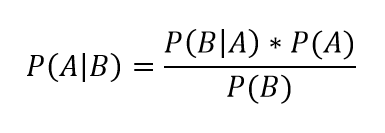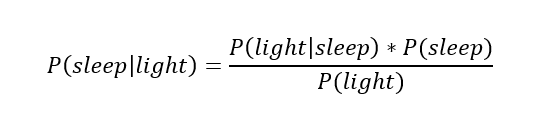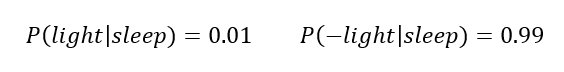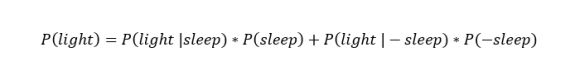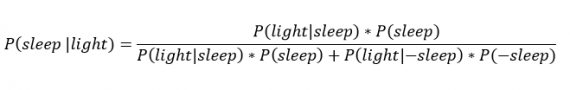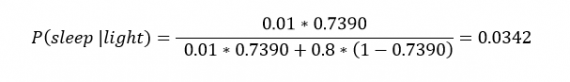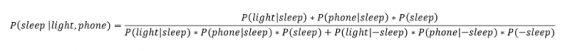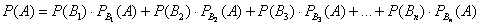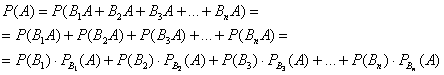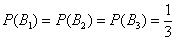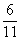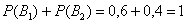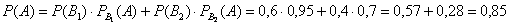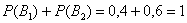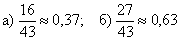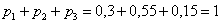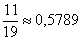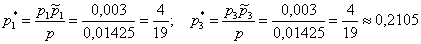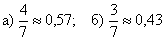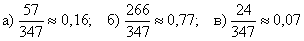Что определяет формула байеса
Формула Байеса
По формуле Байеса можно более точно пересчитать вероятность, беря в расчет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлекшие данное.
Содержание
Теорема [ править ]
Из замечания определения условной вероятности следует, что вероятность произведения двух событий равна:
[math]P(B \cap A)=P(A \cap B)=P(A|B)P(B)[/math]
Если вероятности под знаком суммы известны или допускают экспериментальную оценку, то
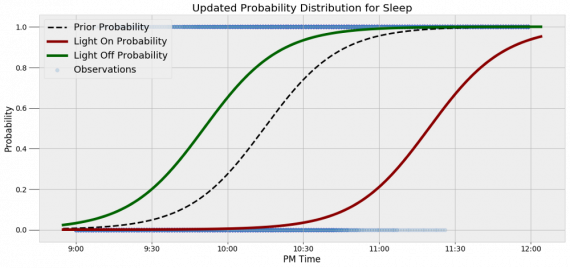
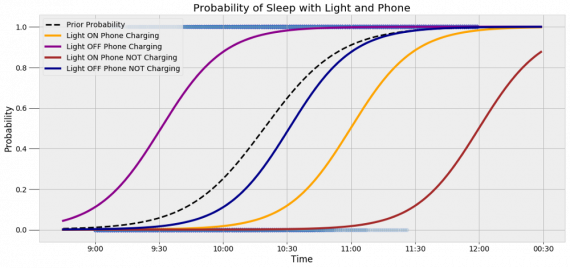
[math]P(B_i|A)=\dfrac Рассмотрим вероятность гриппа при положительном анализе: Вычислим сначала полную вероятность признания больным: [math]0.99 \cdot 0.05 + 0.01 \cdot 0.95 =0.059[/math] Вероятность «здоров» при диагнозе «болен»: [math]P(A|B_1) = \dfrac<0.99 \cdot 0.05><0.99 \cdot 0.05 + 0.01 \cdot 0.95>= 0.839[/math] Таким образом, [math]83.9\%[/math] людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Удивительный результат возникает по причине значительной разницы в долях больных и здоровых. Болезнь [math]N[/math] — редкое явление, поэтому и возникает такой парадокс Байеса. При возникновении такого результата лучше всего сделать повторное обследование. Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, взяв в расчёт как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для её практического применения требуется большое количество расчётов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях. При возникновении теоремы Байеса вероятности, используемые в теореме, подвергались целому ряду вероятностных интерпретаций. В одной из таких интерпретаций говорилось, что вывод формулы напрямую связан с применением особого подхода к статистическому анализу. Если использовать байесовскую интерпретацию вероятности, то теорема показывает, как личный уровень доверия может кардинально измениться вследствие количества наступивших событий. В этом заключаются выводы Байеса, которые стали основополагающими для байесовской статистики. Однако теорема не только используется в байесовском анализе, но и активно применяется для большого ряда других расчётов. Психологические эксперименты [1] показали, что люди часто неверно оценивают реальную (математически верную) вероятность события, основываясь на некоем полученном опыте (апостериорная вероятность), поскольку игнорируют саму вероятность предположения (априорная вероятность). Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого. Возможно, вы никогда не слышали про теорему Байеса, но пользовались ей постоянно. Например, изначально вы оценили вероятность получения прибавки к зарплате как 50%. Получив положительные отзывы от менеджера, вы скорректировали оценку в лучшую сторону, и, наоборот, уменьшили ее, если сломали кофеварку на работе. Так происходит уточнение значения вероятности по мере аккумулирования информации. Основная идея теоремы Байеса состоит в том, чтобы получить большую точность оценки вероятности события путем учета дополнительных данных. Принцип прост: есть первоначальная основная оценка вероятности, которую уточняют c получением большего количества информации. Интуитивные действия формализуются в простом, но мощном уравнении (формула вероятности Байеса): Левая часть уравнения — апостериорная оценка вероятности события А при условии наступления события В (т. н. условная вероятность). Это короткое уравнение является основой байесовского метода. Абстрактность событий А и В не позволяет четко осознать смысл этой формулы. Для понимания сути теоремы Байеса рассмотрим реальную задачу. Одной из тем, над которой я работаю, является изучение моделей сна. У меня есть данные за два месяца, записанные с помощью моих часов Garmin Vivosmart, показывающие, во сколько я засыпаю и просыпаюсь. Окончательная модель, показывающая наиболее вероятное распределение вероятности сна как функцию времени (MCMC — приблизительный метод), приведена ниже. На графике приведена вероятность того, что я сплю, в зависимости лишь от времени. Как она изменится, если учесть время, в течение которого включен свет в спальне? Для уточнения оценки и нужна теорема Байеса. Уточненная оценка основана на априорной и имеет вид: Выражение слева — вероятность того, что я сплю, при условии, что известно, включен ли свет в моей спальне. Априорная оценка в данный момент времени (приведена на графике выше) обозначена как P(sleep). Например, в 10:00 вечера априорная вероятность того, что я сплю, равна 27,34%. Добавим больше информации, используя вероятность P(bedroom light|sleep), полученную из наблюдаемых данных. Из собственных наблюдений мне известно следующее: вероятность того, что я сплю, когда свет включен, равна 1%. Вероятность того, что свет выключен во время сна, равна 1-0,01 = 0,99 (знак «-» в формуле означает противоположное событие), потому что сумма вероятностей противоположных событий равна 1. Когда я сплю, то свет в спальне либо включен, либо выключен. Наконец, уравнение также включает в себя константу нормировки P(light) — вероятность того, что свет включен. Свет бывает включен и когда я сплю, и когда бодрствую. Поэтому, зная априорную вероятность сна, вычислим константу нормировки так: Вероятность того, что свет включен, учтена в обоих вариантах: либо я сплю, либо нет (P (-sleep) = 1 — P (sleep) — это вероятность того, что я не сплю.) Вероятность того, что свет включен в тот момент, когда я не сплю, равна P(light|-sleep), и определяется путем наблюдения. Мне известно, что свет горит, когда я бодрствую, с вероятностью 80% (это означает, что есть 20% вероятность того, что свет не включен, если я бодрствую). Окончательное уравнение Байеса принимает вид: Оно позволяет вычислить вероятность того, что я сплю, при условии, что свет включен. Если нас интересует вероятность того, что свет выключен, нужно каждую конструкцию P(light|… заменить на P(-light|…. Давайте посмотрим, как используют полученные символьные уравнения на практике. Применим формулу к моменту времени 22:30 и учтем, что свет включен. Мы знаем, вероятность того, что я спал, равна 73,90%. Это число — отправная точка для нашей оценки. Уточним его, учтя информацию об освещении. Зная, что свет включен, подставим числа в формулу Байеса: Дополнительные данные резко изменили оценку вероятности: от более 70% до 3,42%. Это показывает силу теоремы Байеса: мы смогли уточнить нашу первоначальную оценку ситуации, включив в нее больше информации. Возможно, мы уже интуитивно делали это раньше, но теперь, рассуждая об этом в терминах формальных уравнений, мы смогли подтвердить наши прогнозы. Рассмотрим еще один пример. Что если на часах 21:45 и свет выключен? Попытайте рассчитать вероятность самостоятельно, считая априорную оценку равной 0.1206. Вместо того, чтобы каждый раз считать вручную, я написал простой код на Python для выполнения этих вычислений, который вы можете попробовать в Jupyter Notebook. Вы получите следующий ответ: The prior probability of sleep: 12.06% И снова дополнительная информация меняет нашу оценку. Теперь, если моя сестра захочет позвонить мне в 21:45 зная, что мой свет включен, она может воспользоваться этим уравнением, чтобы определить, смогу ли я взять трубку (предполагая, что я беру трубку только бодрствующим)! Кто говорит, что статистика неприменима повседневной жизни? Наблюдение за вычислениями полезно, но визуализация помогает добиться более глубокого понимания результата. Я всегда стараюсь использовать графики, чтобы генерировать идеи, если они сами не приходят при простом изучении уравнений. Мы можем визуализировать априорное и апостериорное распределения вероятности сна с использованием дополнительных данных: Когда свет включен, график смещается вправо, указывая на то, что я с меньшей вероятностью сплю в данный момент времени. Аналогично, график смещается влево, если мой свет выключен. Понять смысл теоремы Байеса непросто, но эта иллюстрация наглядно демонстрирует, зачем ее нужно использовать. Формула Байеса — инструмент для уточнения прогнозов с помощью дополнительных данных. Зачем останавливаться на освещении в спальне? Мы можем использовать еще больше данных в нашей модели для дальнейшего уточнения оценки (пока данные остаются полезными для рассматриваемого случая). Например, я знаю, что если мой телефон заряжается, то я сплю с вероятностью 95%. Этот факт можно учесть в нашей модели. Предположим, что вероятность того, что мой телефон заряжается, не зависит от освещения в спальне (независимость событий — это достаточно сильное упрощение, но оно позволит сильно облегчить задачу). Составим новое, еще более точное выражение для вероятности: Получившаяся формула выглядит громоздко, но, используя код на Python, мы можем написать функцию, которая будет производить расчет. Для любого момента времени и любой комбинации наличия освещения/зарядки телефона эта функция возвращает уточненную вероятность того, что я сплю. Пропустим математику (все равно считать будет компьютер) и перейдем к результатам: Time is 11:00:00 PM Light is ON Phone IS NOT charging. The prior probability of sleep: 95.52% В 23:00 без дополнительной информации мы могли почти с полной вероятностью сказать, что я сплю. Однако, как только у нас будет дополнительная информация о том, что свет включен, а телефон не заряжается, мы заключаем, что вероятность того, что я сплю, практически равна нулю. Вот еще один пример: Time is 10:15:00 PM Light is OFF Phone IS charging. The prior probability of sleep: 50.79% Вероятность смещается вниз или вверх в зависимости от конкретной ситуации. Чтобы продемонстрировать это, рассмотрим четыре конфигурации дополнительных данных и то, как они изменяют распределение вероятности: На этом графике представлено много информации, но главный смысл состоит в том, что кривая вероятности изменяется в зависимости от дополнительных факторов. По мере добавления других данных мы будем получать более точную оценку. Теорема Байеса и другие статистические понятия могут быть трудными для понимания, когда они представлены абстрактными уравнениями, использующими только буквы или выдуманные ситуации. Настоящее обучение приходит, когда мы применяем абстрактные понятия в реальных задачах. Успех в области data science — это непрерывное обучение, добавление новых методов в набор навыков и поиск оптимального метода для решения задач. Теорема Байеса позволяет уточнять наши оценки вероятности с помощью дополнительной информации для более качественного моделирования реальности. Увеличение количества информации позволяет получать более точные прогнозы, и метод Байеса оказывается полезным инструментом для решения этой задачи. Я приветствую обратную связь, дискуссию и конструктивную критику. Связаться со мной можно в Twitter: @koehrsen_will. Может быть интересно: Подробно теорема Байеса излагается в отдельной статье. Это замечательная работа, но в ней 15 000 слов. В этом же переводе статьи от Kalid Azad кратко объясняется самая суть теоремы. В статье, на которую дана ссылка в начале этого эссе, разбирается метод диагностики (маммограмма), выявляющий рак груди. Рассмотрим этот метод подробно. Как работать с этим данными? Теперь разберем положительный результат теста. Какова вероятность того, что человек действительно болен: 80%, 90%, 1%? вероятность события = исходы события / все возможные исходы То есть положительный результат маммограммы значит только то, что вероятность наличия заболевания – 7,8%, а не 80% (последняя величина — это лишь предполагаемая точность метода). Такой результат кажется поначалу непонятным и странным, но нужно учесть: метод дает ложноположительный результат в 9,6% случаев (а это довольно много), поэтому в выборке будет много ложноположительных результатов. Для редкого заболевания большинство положительных результатов будут ложноположительными. Давайте пробежимся глазами по таблице и попробуем интуитивно ухватить смысл теоремы. Если у нас есть 100 человек, только у одного из них есть заболевание (1%). У этого человека с 80% вероятностью метод даст положительный результат. Из оставшихся 99% у 10% будут положительные результаты, что дает нам, грубо говоря, 10 ложноположительных исходов из 100. Если мы рассмотрим все положительные результаты, то только 1 из 11 будет верным. Таким образом, если получен положительный результат, вероятность заболевания составляет 1/11. Выше мы посчитали, что эта вероятность равна 7,8%, т.е. число на самом деле ближе к 1/13, однако здесь с помощью простого рассуждения нам удалось найти приблизительную оценку без калькулятора. Теперь опишем ход наших мыслей формулой, которая и называется теоремой Байеса. Эта теорема позволяет исправить результаты исследования в соответствии с искажением, которое вносят ложноположительные результаты: Pr(X) – это константа нормализации. Она сослужила нам хорошую службу: без нее положительный исход испытаний дал бы нам 80% вероятность события. В нашем примере Pr(X) – довольно большое число, потому что велика вероятность ложноположительных результатов. Pr(X) создает результат 7,8%, который на первый взгляд кажется противоречащим здравому смыслу. Мы проводим испытания, чтоб выяснить истинное положение вещей. Если наши испытания совершенны и точны, тогда вероятности испытаний и вероятности событий совпадут. Все положительные результаты будут действительно положительными, а отрицательные — отрицательными. Но мы живем в реальном мире. И в нашем мире испытания дают неверные результаты. Теорема Байеса учитывает искаженные результаты, исправляет ошибки, воссоздает генеральную совокупность и находит вероятность истинного положительного результата. Теорема Байеса удачно применяется в спам-фильтрах. Фильтр берет в расчет результаты испытаний (содержание в письме определенных слов) и предсказывает, содержит ли письмо спам. Всем понятно, что, например, слово «виагра» чаще встречается в спаме, чем в обычных письмах. Фильтр спама на основе черного списка обладает недостатками — он часто выдает ложноположительные результаты. Спам-фильтр на основе теоремы Байеса использует взвешенный и разумный подход: он работает с вероятностями. Когда мы анализируем слова в письме, мы можем рассчитать вероятность того, что письмо — это спам, а не принимать решения по типу «да/нет». Если вероятность того, что письмо содержит спам, равна 99%, то письмо и вправду является таковым. Со временем фильтр тренируется на все большей выборке и обновляет вероятности. Так, продвинутые фильтры, созданные на основе теоремы Байеса, проверяют множество слов подряд и используют их в качестве данных. На данном уроке мы рассмотрим важное следствие теорем сложения и умножения вероятностей и научимся решать типовые задачи по теме. Читателям, которые ознакомились со статьёй о зависимых событиях, будет проще, поскольку в ней мы уже по факту начали использовать формулу полной вероятности. Если Вы зашли с поисковика и/или неважно разбираетесь в теории вероятностей (ссылка на 1-й урок курса), то сначала рекомендую посетить указанные страницы. Собственно, продолжаем. Рассмотрим зависимое событие Эта формула получила название формулы полной вероятности. В учебниках она формулируется теоремой, доказательство которой элементарно: согласно алгебре событий, Наверное, многие предчувствуют содержание первого примера =) Куда ни плюнь – везде урна: Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный? Решение: рассмотрим событие Так как урна выбирается наугад, то выбор любой из трёх урн равновозможен, следовательно: Обратите внимание, что перечисленные гипотезы образуют полную группу событий, то есть, по условию чёрный шар может появиться только из этих урн, а например, не прилететь с бильярдного стола. Проведём простую промежуточную проверку: В первой урне 4 белых + 7 черных = 11 шаров, по классическому определению: Во второй урне только белые шары, поэтому в случае её выбора появление чёрного шара становится невозможным: И, наконец, в третьей урне одни чёрные шары, а значит, соответствующая условная вероятность извлечения чёрного шара составит По формуле полной вероятности: Ответ: Разобранный пример снова наводит на мысль о том, как важно ВНИКАТЬ В УСЛОВИЕ. Возьмём те же задачи с урнами и шарами – при их внешней схожести способы решения могут быть совершенно разными: где-то требуется применить только классическое определение вероятности, где-то события независимы, где-то зависимы, а где-то речь о гипотезах. При этом не существует чёткого формального критерия для выбора пути решения – над ним почти всегда нужно думать. Как повысить свою квалификацию? Решаем, решаем и ещё раз решаем! В тире имеются 5 различных по точности боя винтовок. Вероятности попадания в мишень для данного стрелка соответственно равны 0,5; 0,55; 0,7; 0,75 и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки? Краткое решение и ответ в конце урока. В большинстве тематических задач гипотезы, конечно же, не равновероятны: В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки. Решение: в этой задаче количество винтовок точно такое же, как и в предыдущей, но вот гипотезы всего две: Рассмотрим событие: По формуле полной вероятности: Ответ: 0,85 На практике вполне допустим укороченный способ оформления задачи, который вам тоже хорошо знаком: Решение: по классическому определению: По условию, По формуле полной вероятности: Ответ: 0,85 Следующая задача для самостоятельного решения: Двигатель работает в трёх режимах: нормальном, форсированном и на холостом ходу. В режиме холостого хода вероятность его выхода из строя равна 0,05, при нормальном режиме работы – 0,1, а при форсированном – 0,7. 70% времени двигатель работает в нормальном режиме, а 20% – в форсированном. Какова вероятность выхода из строя двигателя во время работы? На всякий случай напомню – чтобы получить значения вероятностей проценты нужно разделить на 100. Будьте очень внимательны! По моим наблюдениям, условия задач на формулу полной вероятности частенько пытаются подзапутать; и я специально подобрал такой пример. Скажу по секрету – сам чуть не запутался =) Решение в конце урока (оформлено коротким способом) Материал тесно связан с содержанием предыдущего параграфа. Пусть событие При условии, что событие На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть: Рассмотрим это различие на конкретном примере: На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии. Первая часть решения состоит в использовании формулы полной вероятности. Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило. Рассмотрим две гипотезы: Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: Контроль: Рассмотрим зависимое событие: В первой партии 100% – 20% = 80% стандартных изделий, поэтому: Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и По формуле полной вероятности: Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она констатирует тот факт, что событие По формулам Байеса: а) б) После переоценки гипотезы Ответ: Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и находится в одном контейнере. Естественно, Иван Васильевич предварительно подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как уровень доверия. Однако не всё так просто – в байесовском подходе есть и объективное зерно. Ведь вероятности того, что изделие будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и средние оценки. Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и/или 1-й цех снизил), и если проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» 1-й цех и меньше – второй. Предлагаю убедиться в этом самостоятельно: На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%, во второй – 10%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии. Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с Задачей №5, событие «наудачу взятое со склада изделие будет нестандартным» обозначено через Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники. Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает дивиденды и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при этом вероятность противоположной гипотезы («это очередные кидалы»), само собой, уменьшается и уменьшается. Дальнейшее, думаю, понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не только без партии болтов, но и без штанов. К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами: Электролампы изготавливаются на трех заводах. 1-й завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть. Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом? Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае – покупка лампы. Событий прибавилось, и решение удобнее оформить в «быстром» стиле. Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется бракованной. Пользуясь исходными данными, переводим проценты в вероятности: Аналогично: По формуле полной вероятности: Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло) По формуле Байеса: Ответ: Почему изначальная вероятность 2-й гипотезы Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись: Контроль: К слову, о заниженных и завышенных оценках: В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того, что: а) он был подготовлен очень хорошо; Проведите вычисления и проанализируйте результаты переоценки гипотез. Задача приближена к реальности и особенно правдоподобна для группы студентов-заочников, где преподаватель практически не знает способностей того или иного студента. При этом результат может послужить причиной довольно-таки неожиданных последствий (особенно это касается экзаменов в 1-м семестре). Если плохо подготовленному студенту посчастливилось с билетом, то преподаватель с большой вероятностью сочтёт его хорошо успевающим или даже сильным студентом, что принесёт неплохие дивиденды в будущем (естественно, нужно «поднимать планку» и поддерживать свой имидж). Если же студент 7 дней и 7 ночей учил, зубрил, повторял, но ему просто не повезло, то дальнейшие события могут развиваться в самом скверном ключе – с многочисленными пересдачами и балансировкой на грани вылета. Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые руководили делом 100-200 лет назад и прославились своей безупречной репутацией. Да, байесовский подход в известной степени субъективен, но… так устроена жизнь! Закрепим материал заключительным индустриальным примером, в котором я расскажу о до сих пор не встречавшихся технических тонкостях решения: Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит в 2 раза больше деталей, чем второй цех, и в 4 раза больше третьего цеха. В первом цехе брак составляет 12%, во втором – 8%, в третьем – 4%. Для контроля из контейнера берется одна деталь. Какова вероятность того, что она окажется бракованной? Какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех? Таки Иван Васильевич снова на коне =) Должен же быть у фильма счастливый конец =) Решение: в отличие от Задач №№5-8 здесь в явном виде задан вопрос, который разрешается с помощью формулы полной вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие уравнения. За «икс» удобно принять наименьшее значение: Пусть По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет Кроме того, первый цех производит изделий в 2 раза больше, чем второй цех, а значит, доля последнего: Составим и решим уравнение: Контроль: За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдут такими же. Но, так или иначе, самый трудный участок пройден, и решение входит в накатанную колею: Из условия находим: По формуле полной вероятности: Вопрос второй: какова вероятность В данном случае пришлось упрощать четырёхэтажную дробь, что в задачах на формулы Байеса приходится делать довольно часто. Но для данного урока я как-то так случайно подобрал примеры, в которых многие вычисления можно провести без обыкновенных дробей. Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями: Ответ: Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто пытаются затруднить условие, о чём я уже упоминал в начале статьи. Дополнительные примеры есть в файле с готовыми решениями на Ф.П.В. и формулы Байеса, кроме того, наверное, найдутся желающие более глубоко ознакомиться с данной темой в других источниках. А тема действительно очень интересная – чего только стОит один парадокс Байеса, который обосновывает тот житейский совет, что если у человека диагностирована редкая болезнь, то ему имеет смысл провести повторное и даже два повторных независимых обследования. Казалось бы, это делают исключительно от отчаяния… – а вот и нет! Но не будем о грустном. Задача 2: Решение: рассмотрим гипотезы Задача 4: Решение: из условия находим Задача 6: Решение: рассмотрим две гипотезы: По формулам Байеса: Задача 8: Решение: всего: 3 + 19 + 3 = 25 студентов в группе. По классическому определению: Автор: Емелин Александр (Переход на главную страницу) cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5[math]\triangleleft[/math] Примеры [ править ]
Определение вероятности заболевания [ править ]
Парадокс теоремы Байеса [ править ]
Метод фильтрации спама [ править ]
Теорема Байеса
Из Википедии — свободной энциклопедии
Как применять теорему Байеса для решения реальных задач
Формула Байеса
Пример
Python
The updated probability of sleep: 40.44%Визуализация вероятности
Что, если есть еще больше данных?
The updated probability of sleep: 1.74%
The updated probability of sleep: 95.10%Заключение
Простое объяснение теоремы Байеса
Разберемся в методе
Болеют (1%) Не болеют (99%) Положительный результат метода 80% 9,6% Отрицательный результат метода 20% 90,4% Насколько метод точен?
Теорема Байеса
Pr(X) – это вероятность любого положительного результата, будет ли это настоящий положительный результат при исследовании больных (1%) или ложноположительный при исследовании здоровых людей (99%).Смысл теоремы
Спам-фильтр
Формула полной вероятности и формулы Байеса
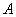
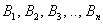
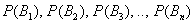
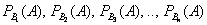
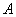
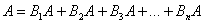
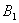
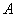
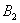
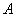
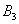
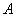
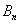
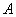
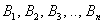
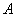
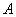
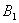
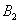
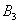
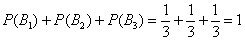
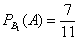
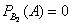
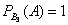
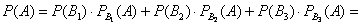
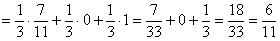
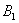
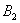
По классическому определению вероятности: 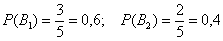
Контроль: 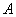
По условию: 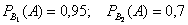
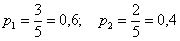
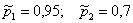
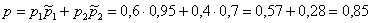
Задачи на формулы Байеса
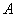
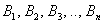
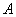
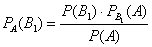
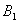
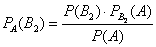
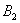
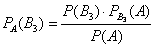
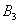
…
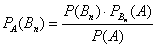
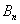
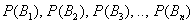
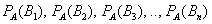
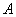
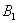
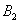
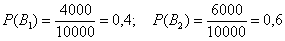
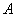
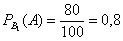
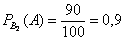
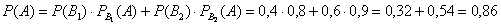
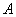
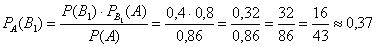
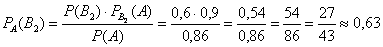
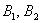
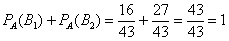
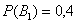
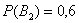
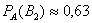
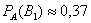
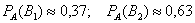
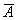
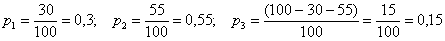
Контроль: 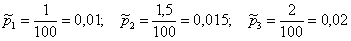
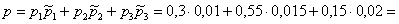
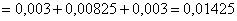
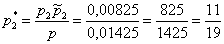
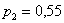
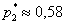
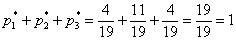
б) был подготовлен средне;
в) был подготовлен плохо.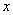
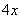
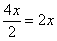
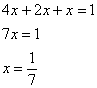
Таким образом: 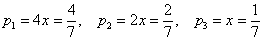
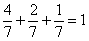
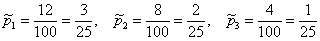
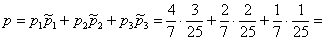
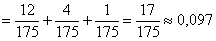
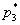
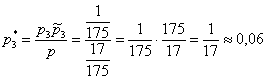
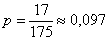
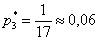
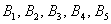
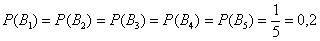
Рассмотрим событие 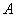
По условию: 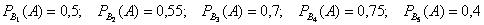
По формуле полной вероятности: 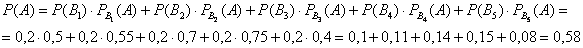
Ответ: 0,58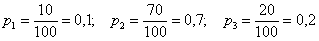
По условию 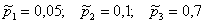
По формуле полной вероятности: 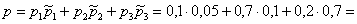
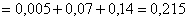
Ответ: 0,215
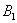
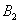
Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: 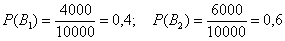
Рассмотрим событие: 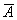
Из условия находим: 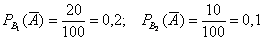
По формуле полной вероятности: 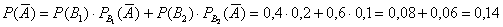
Примечание: данную вероятность легко найти, пользуясь результатом Задачи 5: 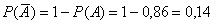
Пусть событие 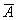
а) 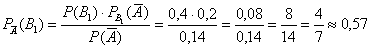
б) 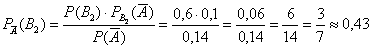
Ответ:
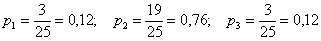
Контроль: 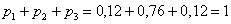
По условию: 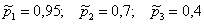
По формуле полной вероятности: 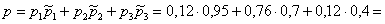
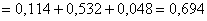
Пусть студент сдал экзамен. По формулам Байеса:
а) 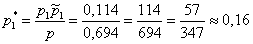
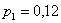
б) 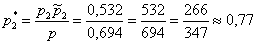
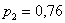
в) 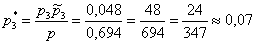
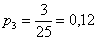
Проверка: 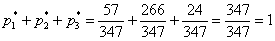
Ответ: