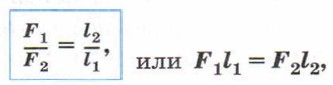Что необходимо для равновесия рычага

Что необходимо для равновесия рычага

1. Что такое рычаг?

Самый простой и распространенный механизм — рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.

2. Как используют рычаг?

Можно для поднятия груза использовать в качестве рычага лом.
Для этого надо с силой F нажимать на конец лома В или приподнимать конец В.
В любом случае при поднятии груза необходимо преодолеть вес груза Р — силу, направленную вертикально вниз.
Для этого надо повернуть лом вокруг оси, проходящей через неподвижную точку лома — точку его опоры О.

Сила F, с которой человек действует на рычаг, меньше силы Р.
Используя рычаг, получаем выигрыш в силе.

2. Что называют плечом силы?

Например, есть рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В.
F1 и F2, действующие на рычаг, направлены в одну сторону.

Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.

3. Как найти плечо силы?

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы.

OA — плечо силы F1,
OB — плечо силы F2.

4. Какое действие оказывают на рычаг силы?

Силы, действующие на рычаг, могут повернуть его вокруг оси или по ходу, или против хода часовой стрелки.
На рисунке выше:
С ила F2 вращает рычаг по ходу часовой стрелки.
Сила F1 вращает рычаг против хода часовой стрелки.
Результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.

5. В чем состоит правило (условие) равновесия рычага?

Правило равновесия рычага было установлено Архимедом (287—212 гг. до н. э.).

Правило (условие) равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

К рычагу по обе стороны от точки опоры подвешивают грузы так, чтобы рычаг оставался в равновесии.
Действующие на рычаг силы равны весам этих грузов.
Далее измеряют модули сил и их плечи.
Если сила F2 уравновешивает силу F1, то плечо меньшей силы в 2 раза больше плеча большей силы.

где
F1 и F2 — силы, действующие на рычаг,
l1 и l2 — плечи этих сил.

6. Как уравновесить меньшей силой большую?

При помощи рычага можно меньшей силой уравновесить большую силу.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.

Задача.
Человеку необходимо поднять с помощью рычага плиту массой 240 кг.
Большее плечо рычага равно 2,4 м.
Меньшее плечо рычага равно 0,6 м.
Какую силу надо приложить человеку к большему плечу рычага?

Человек преодолевает силу 2400 Н, прикладывая свою силу, равную 600 Н.
Здесь рычаг дает выигрыш в силе в 4 раза.
Однако плечо, на которое действует человек, в 4 раза длиннее того, на которое действует вес плиты:
2,4 м : 0,6 м = 4.

Источник

Момент силы. Условия равновесия рычага

п.1. Устройство и виды рычагов

Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.

Рычаг состоит из перекладины и опоры.
Точка опоры делит перекладину рычага на два плеча рычага.

Назначение рычага – получить выигрыш в силе или расстоянии.
Если к плечу рычага достаточно приложить меньшую силу, то переместить конец рычага придётся на бóльшее расстояние: выигрыш в силе оборачивается проигрышем в расстоянии.
И наоборот, если удаётся сократить перемещение конца рычага, придётся приложить бóльшую силу: выигрыш в расстоянии оборачивается проигрышем в силе.

В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.

Рычаг 1-го рода Опора располагается между точками приложения сил Даёт выигрыш в силе	Рычаг 2-го рода Точки приложения сил располагаются по одну сторону от опоры, нагрузка приложена между точкой опоры и точкой приложения силы Даёт выигрыш в силе
Рычаг 3-го рода Точки приложения сил располагаются по одну сторону от опоры, усилие приложено между точкой опоры и нагрузкой. Проигрыш в силе – выигрыш в расстоянии

п.2. Момент силы

Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.

Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.

Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.

п.3. Правило моментов для двух сил

п.4. Правило моментов для нескольких сил

п.5. Применение рычагов в быту и технике

Рычаги первого рода

Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры.	Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект.
Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя.	Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз.
Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом.	Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям.

Рычаги второго рода

Тачка Небольшое усилие, приложенное к ручкам тачки, поднимает тяжелый груз, расположенный ближе к колесу.

Открывалка Давление на ручку преодолевает сопротивление крышки бутылки.

Щипцы для орехов Составной рычаг второго рода. Нагрузка — сопротивление скорлупы.

Рычаги третьего рода

Молоток Точка опоры — плечевой сустав (рука — продолжение рукоятки), а нагрузка — сопротивление дерева. Во время удара по гвоздю головка молотка двигается быстрее, чем рука с рукояткой.	Удочка Одна рука прикладывает усилие для движения удочки, вторая становится точкой опоры. Нагрузка — это вес рыбы, который поднимается на большую высоту легким движением руки.
Пинцет Составной рычаг третьего рода. На кончиках пинцета усилие меньше, чем со стороны пальцев, так что можно захватывать хрупкие предметы. Нагрузка — сопротивление предмета.

п.6. Задачи

Задача 1. Для каждого положения тела укажите плечо силы.

При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.

Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.

Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?

По правилу моментов \begin F_1l_1=F_2l_2. \end Получаем систему уравнений \begin \left\< \begin 15l_1=60l_2 \\ l_1+l_2=1 \end \right. \Rightarrow \left\< \begin l_1=4l_2 \\ l_1+l_2=1 \end \right. \Rightarrow \left\< \begin l_1=4l_2 \\ 4l_2+l_2=1 \end \right. \Rightarrow \\[7pt] \Rightarrow \left\< \begin l_1=4l_2 \\ 5l_2=1 \end \right. \Rightarrow \left\< \begin l_1=0,8 \\ l_2=0,2 \end \right. \end Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.

Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите \(g\approx 10\ \text<м/с>^2\). Ответ запишите в килоньютонах.

Сила тяжести \(F_<\text<т>>=mg\), направленная вниз, уравновешивается силами реакции опор \(F_A\) и \(F_B\), направленными вверх. \begin F_A+F_B=mg \end По правилу моментов при равновесии \begin F_A\cdot OA=F_B\cdot OB=F_B\cdot 4OA\Rightarrow F_A=4F_B \\[7pt] F_A+F_B=5F_B=mg\Rightarrow F_B=\frac <5>\end Получаем: \begin F_B=\frac<500\cdot 10><5>=1000\ \text<Н>=1\ \text<кН>,\ \ F_A=4\cdot 100=4000\ \text<Н>=4\ \text <кН>\end Ответ: 4 кН и 1 кН

п.7. Лабораторная работа №9. Проверка условия равновесия рычага

Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.

Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.

В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.

Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.

Момент силы – это произведение силы, вращающей тело, на её плечо: \(M=Fl\).

Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.

\begin M_1=M_2\\[7pt] F_1l_1=F_2l_2 \end

Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.

Ход работы

1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес \(F_1\).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил \(M_1\) и \(M_2\), их относительные и абсолютные погрешности.
7. Вычислите отношение сил \(\frac\) и плеч \(\frac\) для этого случая, погрешности их определения.
8. Сделайте выводы.

Результаты измерений и вычислений

Выводы
На основании проделанной работы можно сделать следующие выводы.

Отношения сил и плечей равны \begin \frac=2,9\pm 0,2,\ \ \frac=3,0\pm 0,2 \end

Эксперименты подтвердили условие равновесия рычага.

Источник

Правило равновесия рычага

4. На основании подобных опытов более двух тысяч лет назад древнегреческим учёным Архимедом было установлено правило:

рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил.

Это правило (условие) равновесия рычага записывают в виде формулы:

где F₁ и F₂ — силы, действующие на рычаг, l₁ и l₂ — плечи этих сил.

Зная правило равновесия рычага, можно объяснить, как с помощью простого механизма получить выигрыш в силе. Если к длинному концу рычага приложить небольшую силу, то можно уравновесить гораздо большую силу, приложенную к короткому концу рычага.

5. Как можно объяснить выигрыш в силе в примере с тачкой (см. рис. 93), используя правило равновесия рычага?

Силы ₁ и ₂, действующие на тачку, параллельны друг другу и направлены в противоположные стороны. Сила ₂ стремится вращать рычаг по ходу часовой стрелки, а сила ₁ — против её хода.

Плечи сил ₁ и ₂ соответственно равны l₁ и l₂. По правилу равновесия рычага плечо l₂ много меньше плеча l₁, следовательно, чтобы уравновесить рычаг, сила ₁ может быть меньше ₂. Выигрыш в силе очевиден.

6. В основе действия многих машин и механизмов, используемых в быту и технике, лежит правило равновесия рычага. Вы уже знакомы с устройством и принципом действия рычажных весов. Они именно так и называются — «рычажные весы», потому что их основной элемент — рычаг.

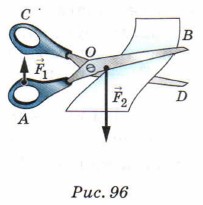
Рассмотрите внимательно обычные ножницы (рис. 96). Они представляют собой пару рычагов, скреплённых в точке О, относительно которой они могут вращаться. Будем считать, что рычаг CD остаётся в покое, а к концу рычага АВ в точке А прикладывается сила ₁ — сила пальцев человека, работающего ножницами. Сила ₂, действующая со стороны рычага на листок бумаги, окажется много больше приложенной силы ₁. На том же принципе основана работа и многих других инструментов: клещей, плоскогубцев, садового секатора и пр.

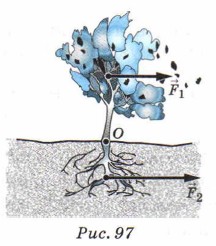
Рычаг встречается повсеместно в живой и неживой природе. Объясняя, например, причину падения деревьев во время урагана, придётся вспомнить о правиле равновесия рычага. Сила сопротивления земли (₂), действующая на корни дерева (рис. 97), может в какой-то момент оказаться недостаточной, чтобы удержать дерево в равновесии, и дерево упадёт под напором порыва ветра (сила ₁).

В организме человека и животного, в теле птиц и насекомых очень много различных рычагов. Только в вашем теле более 200 различных костных рычагов. Очень интересный вывод можно сделать, рассмотрев действие рычага в локтевом суставе человека (рис. 98). В этом рычаге точка опоры (точка О) находится в суставе. Вес груза ₂ приложен к концу рычага, а сила ₁, необходимая для удержания груза, приложена вблизи от точки О. Сила ₁ возникает благодаря сокращению мышц руки человека. В соответствии с правилам равновесия рычага сила ₁ должна быть много больше силы ₂, так как плечо l₁ намного меньше плеча l₂. В данном случае рычаг даёт проигрыш в силе, но выигрыш в расстоянии. Оказывается, сила мышц руки человека гораздо больше веса груза, который он поднимает рукой.

Источник

Правило равновесия рычага

Еще до Нашей Эры люди начали применять рычаги в строительном деле. Например, на рисунке вы видите использование рычага при постройке пирамид в Египте. Рычагом называют твердое тело, которое может вращаться вокруг некоторой оси. Рычаг — это необязательно длинный и тонкий предмет. Например, колесо — тоже рычаг, так как это твердое тело, вращающееся вокруг оси.

Введем еще два определения. Линией действия силы назовем прямую, проходящую через вектор силы. Кратчайшее расстояние от оси рычага до линии действия силы назовем плечом силы. Из курса геометрии вы знаете, что кратчайшее расстояние от точки до прямой — это расстояние по перпендикуляру к этой прямой.

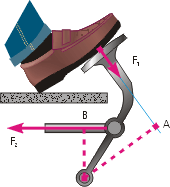
Проиллюстрируем эти определения примером. На рисунке слева рычагом является педаль. Ось ее вращения проходит через точку О. К педали приложены две силы: F1 — сила, с которой нога давит на педаль и F2 — сила упругости натянутого троса, прикрепленного к педали. Проведя через вектор F1 линию действия силы (изображена голубым цветом), и, опустив на нее перпендикуляр из т. О, мы получим отрезок ОА — плечо силы F1.

С силой F2 дело обстоит еще проще: линию ее действия можно не проводить, так как вектор этой силы расположен более удачно. Опустив из т. О перпендикуляр на линию действия силы F2, получим отрезок ОВ — плечо этой силы.

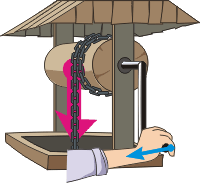
При помощи рычага можно маленькой силой уравновесить большую силу. Рассмотрим, например, подъем ведра из колодца. Рычагом является колодезный ворот — бревно с прикрепленной к нему изогнутой ручкой. Ось вращения ворота проходит сквозь бревно. Меньшей силой служит сила руки человека, а большей силой — сила, с которой ведро и свисающая часть цепи тянет вниз.

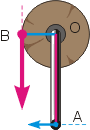
На чертеже слева показана схема ворота. Вы видите, что плечом большей силы является отрезок OB, а плечом меньшей силы — отрезок OA. Ясно видно, что OA > OB. Другими словами, плечо меньшей силы больше плеча большей силы. Такая закономерность справедлива не только для ворота, но и для любого другого рычага. В более общем виде она звучит так:

При равновесии рычага плечо меньшей силы во столько раз больше плеча большей силы, во сколько раз большая сила больше меньшей.

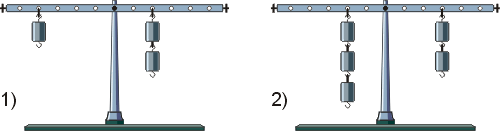
Проиллюстрируем это правило при помощи школьного рычага с грузиками. Взгляните на рисунок. У первого рычага плечо левой силы в 2 раза больше плеча правой силы, следовательно, и правая сила в два раза больше левой силы. У второго рычага плечо правой силы в 1.5 раза больше плеча левой силы, то есть во столько же раз, во сколько левая сила больше правой силы.

Итак, при равновесии на рычаге двух сил бо’льшая из них всегда имеет меньшее плечо и наоборот.

Источник