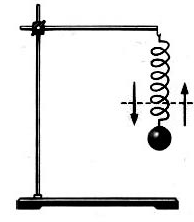
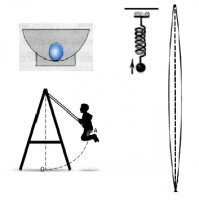
Что называют затухающими колебаниями почему свободные механические колебания всегда затухают
Затухающие колебания
Определение и причины затухания колебаний
Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха
и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической) расходуется на работу против сил трения. В конечном итоге на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально.
Рассматривая свободные гармонические колебания, мы имели дело с идеальными, строго периодическими собственными колебаниями. Описывая при помощи такой модели реальные колебания, мы сознательно допускаем неточность в описании. Однако подобное упрощение является пригодным в силу того, что у многих колебательных систем затухания колебаний, вызванные трением, действительно малы: система успевает совершить много колебаний прежде, чем их амплитуда уменьшится заметным образом.
Графики затухающих колебаний
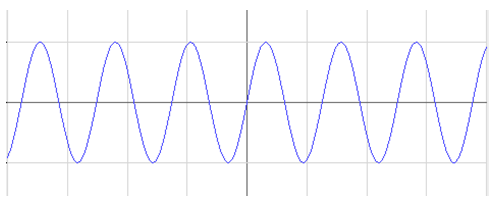
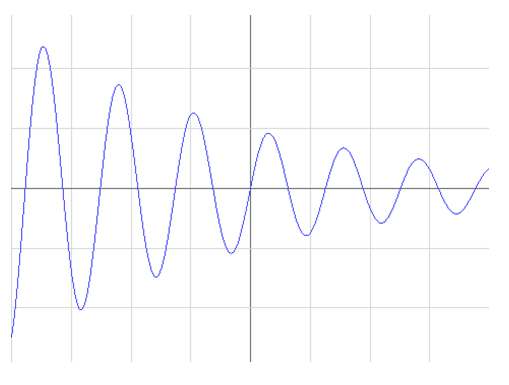
При наличии затухания собственное колебание (рис.1) перестает быть гармоническим. Более того, затухающее колебание перестает быть периодическим процессом — трение влияет не только на амплитуду колебаний (то есть является причиной затухания), но и на продолжительность размахов. С увеличением трения время, необходимое системе для совершения одного полного колебания, увеличивается. График затухающих колебаний представлен на рис. 2.
Рис.1. График свободных гармонических колебаний
Рис.2. График затухающих колебаний
Характерной чертой колебательных систем является то, что небольшое трение влияет на период колебаний в гораздо меньшей степени, чем на амплитуду. Это обстоятельство сыграло огромную роль в усовершенствовании часов. Первые часы с маятником построил голландский физик и математик Христиан Гюйгенс в 1673 г. Этот год можно считать датой рождения современных часовых механизмов. Ход часов с маятником мало чувствителен к изменениям, обусловленным трением, которые в общем случае зависят от многих факторов, в то время как скорость хода предшествующих безмаятниковых часов очень сильно зависела от трения.
На практике возникает потребность как в уменьшении, так и в увеличении затухания колебаний. К примеру, при конструировании часовых механизмов стремятся уменьшить затухание колебаний балансира часов. Для этого ось балансира снабжают острыми наконечниками, которые упираются в хорошо отполированные конические подпятники, выполненные из твердого камня (агата или рубина). Наоборот, во многих измерительных приборах очень желательно, чтобы подвижная часть устройства устанавливалась в процессе измерений быстро, но совершая большого числа колебаний. Для увеличения затухания в этом случае применяют различные демпферы – устройства, увеличивающие трение и, в общем случае, потерю энергии.
Причины затухания свободных колебаний (3 фото)
О том, что свободные колебания являются затухающими, известно из школьного курса физики. Почему они затухают, и возможно ли существование незатухающих колебаний?
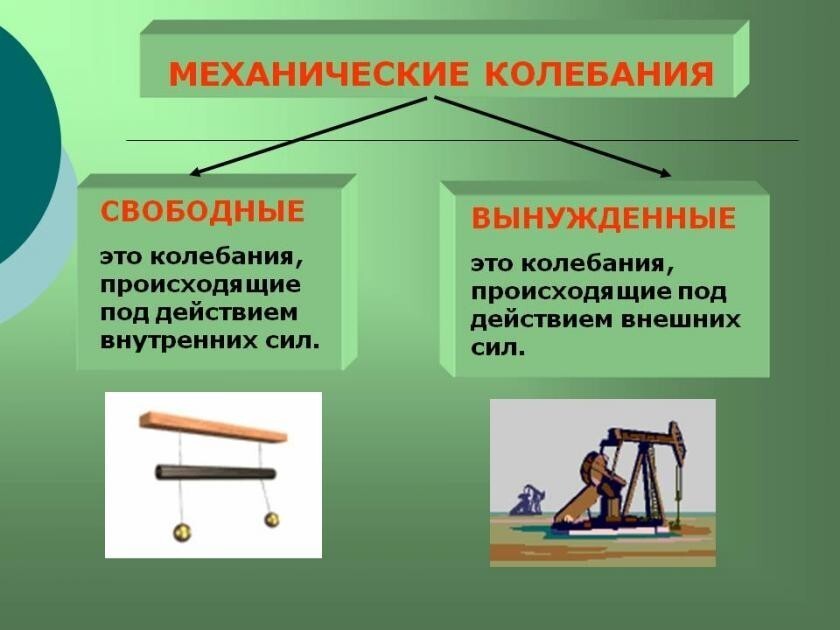
Колебания представляют собой состояние системы вокруг определенного положения равновесия. Для их начала системе необходим первоначальный импульс. А в последующем система может вести себя по-разному: как сразу вернуться в состояние равновесия, так и совершать определенное количество колебательных движений. Описанные виды колебаний носят название вынужденных и свободных. Первые совершаются под влиянием внешней силы, а вторые – под влиянием внутренних сил. Под затуханием свободных колебаний принято понимать плавное снижение амплитуды колебаний с течением времени. Главная причина состоит в потере энергии колебательной системой.
Условия возникновения свободных колебаний
Чтобы возникли свободные колебания, необходимо вывести систему из равновесия, обеспечить при отклонениях действие силы, стремящейся вернуть систему в исходное состояние. При этом потери в системе должны быть минимальны, поскольку только при соблюдении этого условия возвращающая систему в состояние равновесия энергия будет теряться медленно. Свободные колебания – это раскачивающийся маятник, часовой балансир, скачущий мяч, звенящая струна. В зависимости от того, полезны или вредны колебания, для их усиления или ослабления принимают соответствующие меры. Так, в случае с часовым маятником снижают потери, а с деталями и агрегатами механизмов и устройств используют специальные элементы – демпферы и амортизаторы.
Причины колебаний в разных системах
Собственные незатухающие колебания – это, скорее, теоретическое явление. В разных системах и причины затухания колебания будут разными. К примеру, в случае с механической это наличие трения, а в случае с электромагнитным контуром – потеря тепла в проводниках, которые формируют систему.
Когда будут израсходована вся энергия, запасенная колебательной системой, завершатся и колебания. Амплитуда их движения будет снижаться и стремиться к нулю до тех пор, пока не достигнет этого показателя.
Затухающие колебания (собственные и присутствующие в системах) можно рассматривать с одной и той же позиции – общих качеств. Но при этом такие признаки как период и амплитуда нуждаются в переопределении, а прочие требуют дополнения и уточнения, если сравнивать их с аналогичными признаками собственных незатухающих колебаний.
Общие характеристики затухающих колебаний
— амплитуду затухающих колебаний определяет время;
— их частота и период находятся в зависимости от степени затухания;
— фаза и начальная фаза обладают тем же смыслом, что и в случае с незатухающими.
Существуют ли условия, в которых свободные колебания будут незатухающими?
Чтобы колебания были именно свободными, необходимо исключить любые силы, действующие на систему, помимо возвращающей. Чтобы сделать их незатухающими, необходимо восполнять потерю энергии. Сделать это можно, если прилагать к телу периодическую внешнюю силу.
Учебники
Журнал «Квант»
Общие
§17. Механические колебания
17.5 Затухающие колебания.
Рассмотренные свободные незатухающие колебания являются идеализацией, моделью применимой на небольших временных интервалах. В реальных механических колебательных системах обязательно присутствуют диссипативные силы (силы трения, силы вязкости), приводящие к уменьшению механической энергии системы из-за ее перехода в другие формы, например, в тепловую. В данном разделе мы рассмотрим описание колебательного движения при наличии таких сил.
17.5.1 Затухание под действием силы сухого трения.
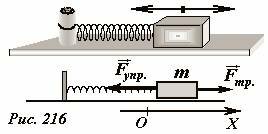
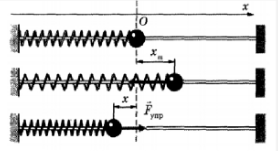
Рассмотрим характер движения пружинного маятника (Рис. 216) с учетом силы сухого трения. Будем считать, что сила, действующая на брусок со стороны горизонтальной поверхности, подчиняется закону Кулона-Амонтона. Коэффициент трения обозначим μ, будем считать, что он не зависит от скорости движения бруска, также пренебрежем различием между трением скольжения и максимальным трением покоя.
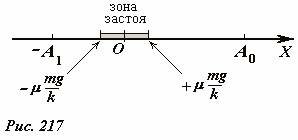
Совмести ось Ox с направлением движения бруска, а ее начало с положением недеформированной пружины. При отклонении бруска на расстояние x, на него в горизонтальном направлении будут действовать силы упругости и сила трения (Рис. 217). Если в этом положении сила упругости \(F_
брусок может находиться в покое, если его скорость равна нулю, поэтому этот интервал является зоной застоя. Пусть начальное отклонение бруска равно A0 лежит вне зоны застоя, начальную скорость будем полагать равной нулю. В этом случае уравнение движения бруска имеет вид (см. рис. 216)
Это уравнение является уравнением гармонических колебаний для величины \(
\omega = \sqrt<\frac
откуда следует закон движения бруска
Скорость бруска будет изменяться по закону
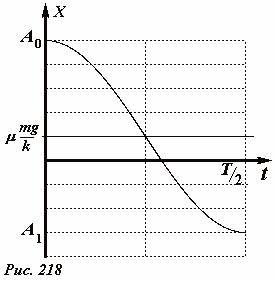
Обратите внимание, что координата точки остановки может быть как положительной, так и отрицательной в зависимости от величины начального отклонения. График закона на временном интервале \(
t \le \frac
\mu \frac
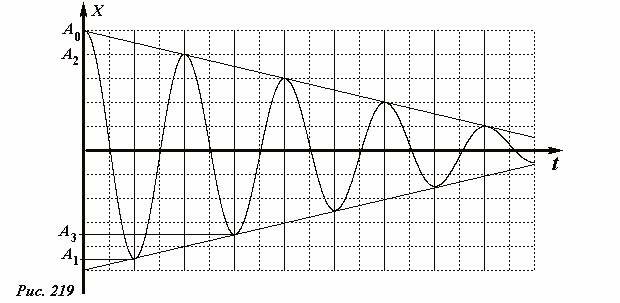
На Рис. 219 показан график закона движения бруска при относительно малом коэффициенте трения, «сшитый» из участков синусоид, аналогичных рассмотренной выше. Между последовательными остановками отклонение бруска уменьшается на постоянную величину
до тех пор пока очередная точка остановки не попадет в область застоя.
Таким образом, постоянная по модулю сила трения не изменяет частоту колебаний, но приводит к уменьшению амплитуды колебаний, причем это уменьшение происходит по линейному закону.
Здесь необходимо сделать одно филологическое замечание. Процесс затухающих колебаний не является периодическим, поэтому использование таких понятий, как период, частота, амплитуда колебаний, строго говоря, не оправдано. Однако при малом затухании эти термины используются: в этом случае под переменной амплитудой колебаний можно понимать отклонение от положения равновесия в моменты остановки, периодом колебаний можно считать промежуток времени между двумя максимальными отклонениями (пусть и различными) в одну сторону. Конечно, при сильном трении (или малом начальном отклонении) движение может содержать только одну фазу: в одну сторону до остановки. Сколько должно быть возвращений два, три. чтобы движение можно было считать колебательным, решайте самостоятельно.
Рассмотрим теперь превращения различных форм энергии в процессе затухающих колебаний. Начальная энергия пружины \(
U_0 = \frac
Так при движении бруска от положения начального отклонения \(x = A_0\) до границы зоны застоя \(
x = \mu \frac
и количества выделившейся теплоты равна начальной энергии бруска (что непосредственно следует из уравнения (8)):
Аналогично можно описать процессы превращения энергии и на других участках движения. Важно не забывать, что всегда работа является мерой перехода энергии из одной формы в другую.
Так с помощью закона сохранения энергии легко получить координату первой точки остановки. Учитывая, что в этой точке скорость и кинетическая энергия бруска равны нулю, запишем уравнение
смысл которого можно выразить словами [3] : сумма потенциальной энергии системы момент остановки и количества выделившейся теплоты равна начальной энергии системы. Из уравнения (10) следует формула (6) для координаты первой остановки.
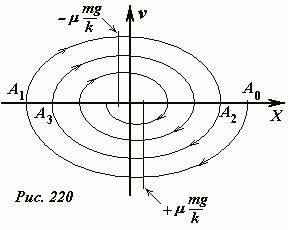
Уравнение закона сохранения энергии (9) позволяет построить фазовую траекторию движения бруска. Путем алгебраических преобразований это уравнение приводится к виду
которое является уравнением эллипса смещенного относительно начала координат. Это уравнение справедливо для первой половины периода колебаний, дальнейшие участки строятся аналогично – результат построения показан на Рис. 220.
17.5.2 Затухание колебаний под действием сил вязкого трения.
Еще одной часто встречающейся причиной затухания колебаний являются силы вязкого трения. Для анализа такого типа движения рассмотрим колебательную систему, показанную на рис. 221. Будем считать, что шарик может двигаться по гладкой горизонтальной поверхности, но в процессе движения на него действует сила сопротивления окружающей среды (например, воздуха). Будем считать, что эта сила пропорциональна скорости движения шарика
Векторная форма записи этого закона, а также отсутствие трения покоя, позволяет рассматривать движение тела во всех его фазах, не зависимо от его направления. Коэффициент пропорциональности в формуле (1) зависит от свойств среды, размеров и формы движущегося тела, в данном разделе мы будем полагать его, как и другие параметры системы известным. Используя традиционные обозначения, запишем уравнение второго закона Ньютона в проекции на горизонтальную ось
Для большей общности незначительно преобразуем этой уравнение, разделив его на массу груза
и введем обозначения появившихся параметров. Величина \(
\frac
При задании начальных условий уравнение (3) может быть решено однозначно, правда сама процедура поиска решения требует определенной математической подготовки, поэтому в нашем изложении мы ее опустим. В явном виде решение уравнения (3) при заданных начальных условиях и не слишком большой силе вязкости имеет вид [5]
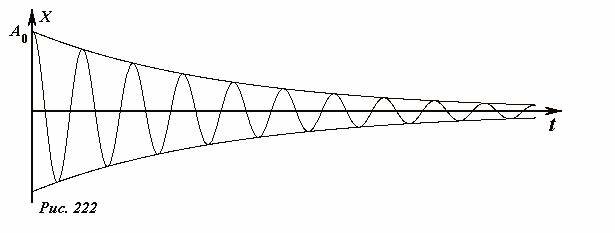
Схематический график этой функции показан на рис. 222.
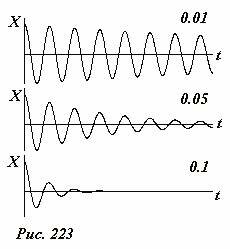
Отметим, наиболее существенные особенности решения уравнения затухающих колебаний (3). Наличие силы вязкого трения приводит к уменьшению амплитуды колебаний. Причем в отличие от рассмотренного затухания под действием силы сухого трения амплитуда убывает нелинейно. Далее мы покажем, что это убывание происходит в геометрической прогрессии. При наличии вязкого трения частота колебаний уменьшается по сравнению с частотой свободных колебаний. Это уменьшение качественно понятно: сила трения замедляет движение, что и приводит к увеличению периода и уменьшению частоты. Если затухание не велико, этим изменением частоты можно пренебречь. Точный вид зависимости частоты от коэффициента затухания дает формула (5). На Рис. 223 показаны несколько графиков решения рассматриваемого уравнения при различных значениях коэффициента затухания. Числа на графиках указывают значение параметра \(
Отметим, что при γ ≥ ω0 движение тела перестает быть колебательным. В этом случае (сильного затухания) тело монотонно стремится к положению равновесия.
Проанализируем теперь процесс затухания колебаний с энергетической точки зрения. Разобьем область движения тела на малые интервалы Δx. В пределах каждого интервала справедливо уравнение (3), которое мы умножим на величину интервала Δx
Выясним теперь смысл каждого слагаемого этого уравнения. Используя определения ускорения и скорости, преобразуем выражение в левой части
Проведенные преобразования показывают, что эта величина есть изменение кинетической энергии шарика. Первое слагаемое в правой части есть работа сила упругости на малом интервале смещения шарика, и она может быть представлена в виде
Полученные результат очевиден: так как сила упругости потенциальна, то работа этой силы равна уменьшению потенциальной энергии пружины.
Наконец последнее слагаемое является работой силы вязкого трения. Эта сила не является потенциальной, поэтому ее работа не может быть выражена через изменение потенциальной энергии. Работа силы трения, взятая с противоположным знаком, равна количеству теплоты, выделившейся на данном интервале
Таким образом, уравнение (6) в виде
допускает очевидное энергетическое истолкование: уменьшение механической энергии системы равно количеству выделившейся теплоты.
При слабом затухании можно приближенно вычислить потери механической энергии. Для этого применим широко распространенный метод, к помощи которого будем прибегать и далее. Еще раз преобразуем выражение для количества выделяющейся теплоты: с помощью соотношения \(\Delta x = \upsilon \Delta t\) перейдем от изменения координаты к временному интервалу Δt
которому соответствует следующая зависимость скорости тела от времени
Следовательно, мощность выделяющейся теплоты изменяется с течением времени по закону
Теперь легко найти среднюю за период колебания мощность тепловых потерь
При выводе последнего соотношения учтено, что среднее значение косинуса за период, очевидно равно нулю.
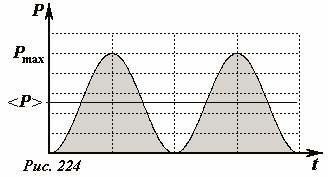
Учитывая, что подобные усреднения нам предстоит неоднократно проделывать в дальнейшем, приведем еще одно наглядное геометрическое доказательство полученного результата. Построим график зависимости мощности от времени \(P = P_
\frac<1> <2>P_
Таким образом, потери механической энергии за один период колебаний равны
Учитывая, что в моменты максимального отклонения скорость шарика обращается в нуль, из уравнения энергетического баланса (10) получим соотношение, описывающее уменьшение амплитуды за одно колебание
Коэффициент в правой части с помощью введенных обозначений преобразуем к виду
с учетом которого перепишем соотношение (16)
Из этого соотношения следует формула
указывающая, что механическая энергия убывает в геометрической прогрессии
Используя связь между энергией и амплитудой колебаний, получим явное выражение для изменения амплитуды
при выводе которого использована приближенная формула \((1 + \xi)^\alpha \approx 1 + \alpha \xi\) для квадратного корня. Формула (18) показывает, что амплитуда колебания также убывает в геометрической прогрессии. Безразмерная величина γT равна относительному уменьшению амплитуды за один период колебания.
Напомним, что полученные выводы справедливы для малого затухания. Теперь можно дать количественный критерий малости затухания, описываемого уравнением (3): приведенный вывод остается справедливым при выполнении условия
Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
Примеры свободных колебаний:
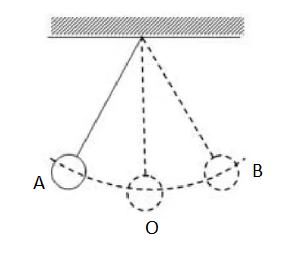
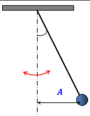
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
Примерами вынужденных колебаний служат:
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
где k — жесткость пружины.
Тогда уравнение движения шарики принимает вид:
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
Начальная скорость равна нулю. Отсюда:
Максимальная скорость равна:
Уравнение движения математического маятника
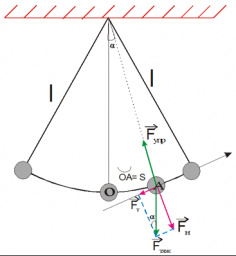
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Разделим обе части выражения на массу шарика m и получим:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
Тогда длина нити равна:
Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
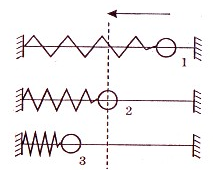
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить