Что называют тропическим годом
Тропический год
Содержание
Продолжительность тропического года
По сильно упрощённому определению, тропический год — это время, необходимое для того, чтобы солнце, начав своё движение от выбранной эклиптической долготы, завершило один полный цикл времён года и возвратилось к той же самой эклиптической долготе. Прежде чем рассматривать пример, следует уточнить понятие равноденствия. При выполнении расчетов в солнечной системе используются две важные плоскости: плоскость эклиптики (орбита Земли вокруг Солнца), и плоскость небесного экватора (проекция экватора Земли в пространстве). Эти плоскости имеют линию пересечения. Направление вдоль этой линии пересечения от Земли в сторону созвездия Овна — это мартовское равноденствие, которое обозначается символом ♈ (символ похож на бараньи рога).
Противоположное направление вдоль линии в сторону созвездия Весов является сентябрьским равноденствием и обозначается символом ♎. Из-за прецессии и нутации земной оси эти направления изменяются по сравнению с направлением на далекие звёзды и галактики, направления на которые не имеют заметного сдвига из-за большого расстояния до этих объектов (см. Международная небесная система отсчета).
Эклиптическая долгота Солнца — это угол между ♈ и Солнцем, измеренный в восточном направлении вдоль эклиптики. Его измерение сопряжено с определёнными трудностями, поскольку Солнце движется, и направление, относительно которого измеряется угол, тоже движется. Для такого измерения удобно иметь фиксированное (по отношению к далеким звёздам) направление. В качестве такого направления выбрано направление ♈ в полдень 1 января 2000, оно обозначается символом ♈0.
С использованием такого сильно упрощенного определения, было зафиксировано весеннее равноденствие 20 марта 2009 года в 11:44:43.6. Следующее равноденствие будет 20 марта 2010 года в 17:33:18.1, что даёт продолжительность тропического года в 365 дней 5 часов 49 минут 30 секунд. Солнце и ♈ движутся в противоположных направлениях. Когда Солнце и ♈ встретятся в марте 2010 в точке равноденствия, Солнце пройдёт в восточном направлении угол 359° 59′ 09″, а ♈ сдвинется в западном направлении на 51″, что в сумме составляет 360° (всё по отношению к ♈0).
Средняя продолжительность тропического года по весеннему равноденствию
Как уже упоминалось выше, продолжительность тропического года зависит от выбора точки отсчета. Астрономы не сразу пришли к единой методике, но чаще всего выбирали в качестве точки отсчёта одно из равноденствий, потому что приборы в эти периоды оказались наиболее чувствительными. При сравнении измерений тропического года за нескольких последовательных лет обнаружены различия, связанные с нутацией и планетарными возмущениями, действующими на Солнце. Миус и Савой в работе [1] приводят следующие примеры интервалов между весенними равноденствиями:
| Дни | Часы | Мин. | Сек. | |
|---|---|---|---|---|
| 1985—1986 | 365 | 5 | 48 | 58 |
| 1986—1987 | 365 | 5 | 49 | 15 |
| 1987—1988 | 365 | 5 | 46 | 38 |
| 1988—1989 | 365 | 5 | 49 | 42 |
| 1989—1990 | 365 | 5 | 51 | 06 |
Сравнение значений средних интервалов времени между равноденствиями и солнцестояниями за астрономический 0 (1 г. до н. э. по традиционному счету) и 2000 года представлено [1] в таблице:
| Год 0 | Год 2000 | |
|---|---|---|
| Между двумя мартовскими равноденствиями | 365,242 137 дней | 365,242 374 дней |
| Между двумя июньскими солнцестояниями | 365,241 726 | 365,241 626 |
| Между двумя сентябрьскими равноденствиями | 365,242 496 | 365,242 018 |
| Между двумя декабрьскими солнцестояниями | 365,242 883 | 365,242 740 |
Текущее значение средней продолжительности тропического года
Средняя продолжительность тропического года с 1 января 2000 года составляет 365,2421897 дней или 365 дней 5 часов 48 минут 45,19 секунды. Эта величина меняется довольно медленно. Выражение, подходящее для вычисления продолжительности тропического года в далёком прошлом:
365.242 189 669 8 − 6.153 59 × 10 ^ −6 T − 7.29 × 10 ^ −10 T 2 + 2.64 × 10 ^ −10 T 3
где Т — время в юлианских столетиях (1 юлианское столетие равно в точности 36525 дней), отсчитываемое от полудня 1 января 2000 года [3] [4]
Календарный год
Григорианский календарь, который используется для гражданских целей, является международным стандартом. Это солнечный календарь (он изобретён для поддержания синхронности с тропическим годом). Он имеет периодичность в 400 лет (146097 дней). В каждом периоде полностью повторяются месяцы, даты и дни недели. Средняя продолжительность календарного года: 146097 / 400 = 365,2425 дней, что даёт хорошее приближение к тропическому году.
Тропический год (также известный как солнечный год) в общем смысле — это отрезок времени, за который Солнце завершает один цикл смены времён года, как это видно с Земли, например, время от одного весеннего равноденствия до следующего, или от одного дня летнего солнцестояния до другого. Со времён античности астрономы постепенно совершенствовали определение тропического года и в настоящее время определяют его как время, необходимое для того, чтобы средняя тропическая долгота Солнца (продольная позиция вдоль эклиптики относительно положения на весеннее равноденствие) увеличилась на 360 градусов (то есть, чтобы завершился один полный сезонный цикл)[
А земному наблюдателю представляется, что Солнце перемещается по небу среди звёзд; так думали в древности, в античные времена и в средневековье.
В июне-июле Солнце далеко смещается в северное полушарие неба, — в то полушарие неба, где расположена Полярная звезда. Поэтому Солнце сильно прогревает северное полушарие Земли, где в это время — лето. Наоборот, в декабре-январе Солнце далеко уходит в южное полушарие неба, поэтому оно прогревает южное полушарие Земли, и лето там, а в северном полушарии Земли в декабре-январе зима.
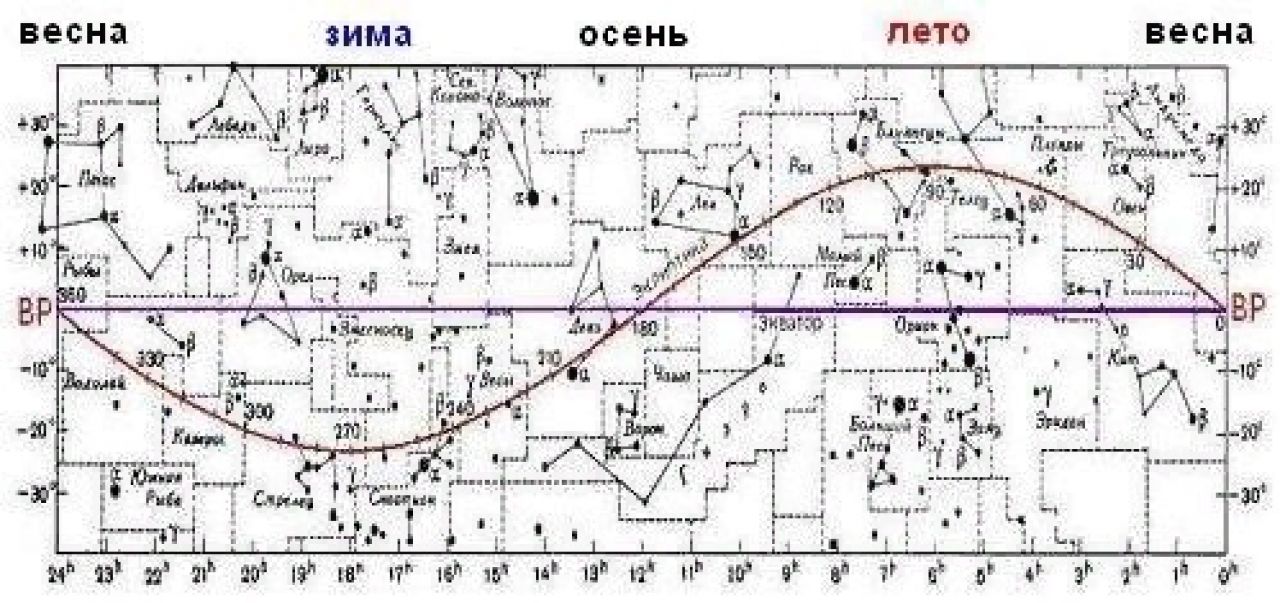
Это наглядно видно на карте экваториальной области неба:
Здесь фиолетовая линия — небесный экватор. Выше него — прилегающая к экватору часть северного полушария неба, ниже — экваториальная часть южного полушария.
Красная линия изображает годовой путь Солнца по небу, называемый эклиптикой * 1. Изображение Солнца на карте перемещается вдоль эклиптики справа налево.
Дважды в год, в дни весеннего (20-21 марта) и осеннего равноденствий (23 сентября), Солнце бывает на небесном экваторе в точках весеннего и осеннего равноденствия. Наверху подписаны сезоны года для северного полушария Земли, когда Солнце находится в соответствующей области неба.
Солнце, проходя через точку весеннего равноденствия, — на карте она обозначена буквами ВР, — попадает из южного полушария неба в северное. Именно момент прохождения Солнца через точку весеннего равноденствия является началом астрономической весны. По своей сути этот момент является переходным от зимы к лету для северного полушария Земли.
Ну, сами посудите, как же может быть иначе? Летом дни длинные, зато ночи короткие, а зимой всё наоборот. В день весеннего равноденствия продолжительности дня и ночи в точности уравниваются. Поэтому момент прохождения Солнца через точку весеннего равноденствия и принят за начало астрономической весны.
Промежуток времени между двумя последовательными прохождениями Солнца через точку весеннего равноденствия называется тропическим годом. Т.е. была весна (в северном полушарии Земли), а потом снова наступит весна.
Это значит, что сезоны года повторяются с периодом, равным тропическому году.
По современным данным его продолжительность на 1 января 2000 года равна 365,2421897 ср. солн. суток или 365 дней 5 часов 48 минут 45,19 секунды.
5. Почему у разных годов разная продолжительность?
— звёздного (сидерического) года 365, 25636 ср. солн. суток,
— аномалистического года 365,2596 ср. солн. суток,
— тропического года 365,2422 ср. солн. суток
С точки зрения геометрии и кинематики именно звёздный год и есть тот самый период, с которым Земля обращается вокруг Солнца.
Орбита, по которой Земля обращается вокруг Солнца, под воздействием планет солнечной системы, особенно таких, как Юпитер и Сатурн, со временем немного меняется. В частности перигелий орбиты Земли очень медленно движется так, что Земле приходится его догонять, а на это требуется время. Поэтому аномалистический год длиннее звёздного.
Тропический год, наоборот, короче звёздного, потому что точка весеннего равноденствия сама медленно движется по небу навстречу Солнцу, следовательно, Солнце и точка весеннего равноденствия встречаются раньше, чем Земля сделает полный оборот вокруг Солнца.
Какой год самый главный? — Правильный ответ вы, наверное, уже и сами знаете.
— В небесной механике естественным образом возникает и поэтому является самым главным аномалистический год.
— Если нужно охарактеризовать обращение Земли вокруг Солнца в пространстве, — то главным является звёздный год.
— В теории солнечных календарей главным является тропический год, потому что сезоны года повторяются с периодом, равным
— Наконец, предсказания солнечных и лунных затмений выполняются на основе т. н. драконического года (346,620 ср. солн. суток).
6. Как измерить продолжительность тропического года?
Древний человек, у которого нет никаких астрономических инструментов, мог бы поступить так. В южной стене прочного помещения или пещеры делается такое отверстие, в которое прямые солнечные лучи в полдень попадают только дважды в год, — весной и осенью, а затем подсчитывается количество прошедших суток и лет.
Количество суток определяется по чередованию дня и ночи. Счёт лет следует начинать от дня появления весеннего солнечного луча, а затем наблюдать следующие появления. При этом нужно иметь в виду, что в какие-то годы наблюдения могут не получиться из-за плохой погоды.
В результате таких примитивных наблюдений станет известно, m суток составляют n лет. Тогда средняя продолжительность тропического года будет приближённо равна дроби m/n.
Спустя 20 лет можно будет утверждать, что продолжительность тропического года приблизительно равна 365,25 суток, что достаточно для создания юлианского календаря. Для создания календаря, подобного григорианскому, придётся наблюдать несколько сотен лет.
И ещё. Для определения продолжительности тропического года можно также наблюдать полуденную высоту Солнца, которая, как известно, минимальна в дни солнцестояний. Известно, что знаменитый древнегреческий астроном Метон для наблюдения солнцестояний воздвигал свои стелы (колонны) и инструменты в Афинах у самой площади народных собраний.
Около 125 до н.э. Гиппарх из Никеи уточнил продолжительность тропического года и синодического месяца, — промежутка времени между двумя последовательными, одинаковыми фазами Луны.
Согласно Гиппарху 304 солнечных года соответствуют 3760 лунным месяцам. Это позволило ему получить более точные значения продолжительности и тропического года, и синодического месяца, приблизив их к истинным значениям.
По данным Гиппарха солнечный год равнялся 365 дням 5ч 55 мин 16 сек, а лунный месяц — 29 дням 12 ч 44 мин 2,5 сек. Первая из этих величин всего лишь на 6 мин 30,41 сек больше принятого в настоящее время значения, а вторая — на 0,5 сек меньше.
Современное значение для продолжительности тропического года таково: на 1 января 2000 года он равен 365,2421897 ср. солн. суток или 365 дней 5 часов 48 минут 45,19 секунды.
7. В чём главная проблема солнечных календарей.
Календарный год должен содержать целое число суток, — альтернативная возможность даже не обсуждается, потому что иначе будет очень неудобно измерять время.
Тропический год длиннее, чем 365 суток на 0,2422 суток. Поэтому, если принять продолжительность календарного года в 365 суток, то новый год будет наступать раньше, чем положено, на 0,2422 суток. За четыре года ошибка достигнет примерно одних суток, за 120 лет она будет равна целому месяцу, а за 360 лет — целому сезону! Это значит, что когда календарь указывает на Новый год, на самом деле ещё осень.
Отсюда понятно: чтобы между сезонами года и календарём не было расхождений, необходимо точное равенство календарного и тропического года.
Итак, календарный год должен содержать целое число суток. Тропический год не содержит целое число суток. Поэтому они не могут быть в точности равны.
Григорианский календарь, который используется для гражданских целей, является международным стандартом. Это солнечный календарь (он изобретён для поддержания синхронности с тропическим годом). Он имеет периодичность в 400 лет (146 097 дней). В каждом периоде полностью повторяются месяцы, даты и дни недели. Средняя продолжительность календарного года: 146 097 / 400 = 365,2425 дней, что даёт хорошее приближение к тропическому году.
Григорианский календарь тоже не совсем точен. Ведь в целях коррекции из чреды дней выбрасывается трое суток за 400 лет, тогда как в действительности такая ошибка, исходя из принятой в настоящее время ве-личины солнечного года набегает всего за 384 (= 128 х 3) года. В результате средняя продолжительность григорианского календарного года составляет 365, 24250 суток. Как видим, она больше действительной её величины (365, 2421988 суток) округлённо на 0, 00030 суток, то есть приблизительно на 26 секунд. Погрешность в целые сутки накапливается за 3280 лет. Вполне очевидно, что на самом деле в григорианском календаре к исходному моменту в цикле не возвращается и равноденствие. Отмечен-ное превышение длины истинного тропического года на 26 секунд за 400 лет составит уже 2 часа 52 минуты 48 секунд, или 0, 12 суток. Именно на такое время истинное весеннее равноденствие в 2000 году наступило раньше, чем оно было в 1600 году.
Экли́птика — большой круг небесной сферы, по которому происходит видимое годичное движение Солнца. Соответственно плоскость эклиптики — плоскость обращения Земли вокруг Солнца (земной орбиты).
*2 Прецессия земной оси
Предварение равноденствий (лат. praecessio **************) — историческое название для постепенного смещения точек весеннего и осеннего равноденствий (то есть точек пересечения небесного экватора с эклиптикой) навстречу видимому годичному движению Солнца. Другими словами, каждый год весеннее равноденствие наступает немного раньше, чем в предыдущем году — примерно на 20 минут 24 секунды. В угловых единицах смещение составляет сейчас примерно 50,3″ в год, или 1 градус каждые 71,6 года. Это смещение является периодическим, и примерно каждые 25776 лет точки равноденствия возвращаются на прежние места.
Тропический год
С древних времен астрономы постепенно уточняли определение тропического года. Запись для слова «год, тропический» в онлайн-глоссарии астрономического альманаха ( 2015 ) гласит:
СОДЕРЖАНИЕ
История [ править ]
Происхождение [ править ]
Слово «тропический» происходит от греческого tropikos, означающего «поворот» ( тропик 1992 г. ). Таким образом, тропики Рака и Козерога отмечают крайние северные и южные широты, где Солнце может появляться прямо над головой и где оно, кажется, «поворачивается» в своем ежегодном сезонном движении. Из-за этой связи между тропиками и сезонным циклом видимого положения Солнца слово «тропический» также дало название «тропическому году». Ранние китайцы, индуисты, греки и другие приблизительно измеряли тропический год.
Раннее значение, обнаружение прецессии [ править ]
Средние века и Возрождение [ править ]
18 и 19 века [ править ]
В таблице приведены два уравнения. Оба уравнения показывают, что тропический год становится короче примерно на полсекунды каждое столетие.
20 и 21 века [ править ]
Продолжительность среднего тропического года выводится из модели солнечной системы, поэтому любое усовершенствование, улучшающее модель солнечной системы, потенциально повышает точность среднего тропического года. Появилось много новых инструментов для наблюдений, в том числе
Шкалы времени и календарь [ править ]
Однако вращение самой Земли нерегулярно и замедляется по отношению к более стабильным индикаторам времени: в частности, движению планет и атомным часам.
Как следствие, тропический год, следующий за сезонами на Земле, считая в солнечных днях UT, все больше не синхронизируется с выражениями для равноденствий в эфемеридах в TT.
| Мероприятие | Год | Ближайший год S&M | Δ T | σ |
|---|---|---|---|---|
| Начало юлианского календаря | -44 | 0 | 2ч56м20с | 4 мин. 20 сек. |
| Первый Никейский собор | 325 | 300 | 2ч8м | 2м |
| Начало григорианского календаря | 1582 | 1600 | 2м | 20 с |
| экстраполяция с низкой точностью | 4000 | 4ч13м | ||
| экстраполяция с низкой точностью | 10 000 | 2d11h |
Экстраполяции с низкой точностью вычисляются с помощью выражения, предоставленного Morrison & Stephenson (2004).
Δ T в секундах = −20 + 32 t 2
Продолжительность тропического года [ править ]
Средний промежуток времени между равноденствиями [ править ]
| дней | часы | мин | s | |
|---|---|---|---|---|
| 1985–1986 | 365 | 5 | 48 | 58 |
| 1986–1987 | 365 | 5 | 49 | 15 |
| 1987–1988 | 365 | 5 | 46 | 38 |
| 1988–1989 | 365 | 5 | 49 | 42 |
| 1989–1990 | 365 | 5 | 51 | 06 |
Различные определения тропического года [ править ]
«Средний тропический год» основан на среднем значении солнца и не в точности равен любому времени, которое требуется для перехода от равноденствия к следующему или от одного солнцестояния к следующему.
| Год 0 | 2000 год | |
|---|---|---|
| Между двумя северными равноденствиями | 365.242 137 дней | 365,242 374 дня |
| Между двумя северными солнцестояниями | 365,241 726 | 365,241 626 |
| Между двумя равноденствиями, направленными на юг | 365,242 496 | 365,242 018 |
| Между двумя южными солнцестояниями | 365,242 883 | 365,242 740 |
| Средний тропический год (выражение Ласкара) | 365,242 310 | 365,242 189 |
Текущее значение среднего тропического года [ править ]
Календарный год [ править ]
А тропический год (также известный как солнечный год) это время что солнце нужно вернуться к тому же позиция в цикле сезоны, как видно из земной шар; например, время от весеннее равноденствие до весеннего равноденствия или от летнее солнцестояние к летнему солнцестоянию. Это отличается от времени, за которое Земля совершает один полный оборот вокруг Солнца, измеряемого по отношению к фиксированные звезды (в звездный год) примерно на 20 минут из-за прецессия равноденствий.
С древних времен астрономы постепенно уточняли определение тропического года. Запись для «тропический год» в Онлайн-глоссарий астрономического альманаха (2015) состояния:
период увеличения эклиптической долготы Солнца на 360 градусы. Поскольку эклиптическая долгота Солнца измеряется по отношению к равноденствию, тропический год включает полный цикл сезонов, а его длина в долгосрочном плане приближается к гражданскому (григорианскому) календарю. Средний тропический год составляет примерно 365 дней 5 часов 48 минут 45 секунд.
Эквивалентное, более описательное определение: «Естественной основой для вычисления уходящих тропических лет является средняя долгота Солнца, отсчитываемая от прецессионно движущегося равноденствия (динамического равноденствия или равноденствия даты). Когда долгота достигает значения, кратного 360 градусам, означает, что Солнце пересекает точку весеннего равноденствия и начинается новый тропический год »(Борковский 1991, п. 122).
Средний тропический год в 2000 году составил 365,24219. эфемеридные дни; продолжительность каждого эфемеридного дня 86 400 секунд СИ. [1] Это 365,24217 средние солнечные дни (Ричардс 2013, п. 587).
Содержание
История
Источник
Слово «тропический» происходит от Греческий тропикос значение «поворот» (тропик 1992). Таким образом, тропики Рак и Козерог отметьте крайний север и юг широты где Солнце может появляться прямо над головой и где оно, кажется, «поворачивается» в своем ежегодном сезонном движении. Из-за этой связи между тропиками и сезонным циклом видимого положения Солнца слово «тропический» также дало название «тропическому году». Ранние китайцы, индуисты, греки и другие приблизительно измеряли тропический год.
Ранняя оценка, открытие прецессии
Во 2 веке до нашей эры. Гиппарх измерил время, необходимое Солнцу, чтобы пройти от равноденствие к тому же равноденствию снова. Он подсчитал, что продолжительность года составляет 1/300 дня меньше 365,25 дня (365 дней, 5 часов, 55 минут, 12 секунд или 365,24667 дней). Гиппарх использовал этот метод, потому что он мог лучше определять время равноденствий, чем солнцестояний (Meeus & Savoie 1992, п. 40).
Средние века и эпоха Возрождения
В средние века и в эпоху Возрождения был опубликован ряд все более совершенных таблиц, которые позволяли вычислять положения Солнца, Луна и планеты относительно неподвижных звезд. Важным применением этих таблиц было реформа календаря.
В Таблицы Альфонсин, опубликованные в 1252 году, основывались на теориях Птолемей и были пересмотрены и обновлены после первоначальной публикации; самое последнее обновление в 1978 г. было сделано Французский национальный центр научных исследований. Продолжительность тропического года составила 365 солнечных дней 5 часов 49 минут 16 секунд (≈ 365,24255 дней). Эта длина была использована при разработке Григорианский календарь из 1582 г. (Meeus & Savoie 1992, п. 41).
В 16 веке Коперник выдвинул гелиоцентрическая космология. Эразм Рейнхольд использовал теорию Коперника для вычисления Прутеновые таблицы в 1551 году, и дал тропический год длиной 365 солнечных дней, 5 часов, 55 минут, 58 секунд (365,24720 дней), исходя из длины звездный год и предполагаемая скорость прецессии. На самом деле это было менее точным, чем предыдущее значение таблиц Альфонсина.
Основные успехи в 17 веке были сделаны Иоганн Кеплер и Исаак Ньютон. В 1609 и 1619 годах Кеплер опубликовал свои три закона движения планет (Маккарти и Зайдельманн, 2009 г., п. 26). В 1627 году Кеплер использовал наблюдения Тихо Браге и Waltherus для создания наиболее точных на тот момент таблиц, Таблицы Рудольфина. Он оценил средний тропический год как 365 солнечных дней, 5 часов 48 минут 45 секунд (365,24219 дней; Meeus & Savoie 1992, п. 41).
Три закона динамики Ньютона и теория гравитации были опубликованы в его Philosophiæ Naturalis Principia Mathematica в 1687 году. Теоретические и математические достижения Ньютона повлияли на таблицы Эдмонд Галлей опубликовано в 1693 и 1749 гг. (Маккарти и Зайдельманн, 2009 г., pp. 26–28) и послужили основой для всех моделей Солнечной системы до Альберт Эйнштейнтеория Общая теория относительности в 20 веке.
18 и 19 века
Со времен Гиппарха и Птолемея год основывался на двух равноденствиях (или двух солнцестояниях) с разницей в несколько лет, чтобы усреднить как ошибки наблюдений, так и периодические вариации (вызванные гравитационным притяжением планет и небольшим влиянием нутация в день равноденствия). Эти эффекты стали понятны только во времена Ньютона. Чтобы смоделировать краткосрочные вариации времени между равноденствиями (и не допустить, чтобы они мешали измерению долгосрочных вариаций), требуются точные наблюдения и сложная теория видимого движения Солнца. Необходимые теории и математические инструменты соединились в 18 веке благодаря работе Пьер-Симон де Лаплас, Жозеф Луи Лагранж, и другие специалисты в небесная механика. Они смогли вычислить периодические изменения и отделить их от постепенного среднего движения. Они могли выразить среднюю долготу Солнца в виде полинома, например:
куда Т время в юлианских веках. Производная этой формулы является выражением средней угловой скорости, а обратная ей величина дает выражение для длины тропического года как линейной функции от Т.
В таблице приведены два уравнения. Оба уравнения показывают, что тропический год становится короче примерно на полсекунды каждое столетие.
| Имя | Уравнение | Дата, когда Т = 0 |
|---|---|---|
| Леверье (Meeus & Savoie 1992, п. 42) | Y = 365.242 196 47 − 6.24 × 10 − 6 Т | 0.5 января 1900 г. Эфемеридное время |
| Newcomb (1898) | Y = 365.242 198 79 − 6.14 × 10 − 6 Т | 0 января 1900 г., среднее время |
Таблицы Ньюкомба были достаточно точными, чтобы их использовали совместные американско-британские Астрономический альманах для Солнца, Меркурий, Венера, и Марс до 1983 г. (Зайдельманн 1992, п. 317).
20 и 21 века
Продолжительность среднего тропического года выводится из модели солнечной системы, поэтому любое усовершенствование, улучшающее модель солнечной системы, потенциально повышает точность среднего тропического года. Появилось много новых инструментов для наблюдений, в том числе
Сложность модели, используемой для солнечной системы, должна быть ограничена доступными вычислительными средствами. В 1920-х годах оборудование для перфокарт вошло в употребление L. J. Comrie в Великобритании. Для Американские эфемериды электромагнитный компьютер, Электронный калькулятор выборочной последовательности IBM использовался с 1948 года. Когда стали доступны современные компьютеры, стало возможным вычислять эфемериды, используя численное интегрирование а не общие теории; численное интегрирование вошло в употребление в 1984 г. для совместных американо-британских альманахов (Маккарти и Зайдельманн, 2009 г., п. 32).
Альберт Эйнштейнс Общая теория относительности предоставили более точную теорию, но точность теорий и наблюдений не требовала уточнения, обеспечиваемого этой теорией (за исключением продвижения перигелия Меркурия) до 1984 года. Шкалы времени включали общую теорию относительности, начиная с 1970-х годов (Маккарти и Зайдельманн, 2009 г., п. 37).
Ключевым достижением в понимании тропического года в течение длительных периодов времени является открытие того факта, что скорость вращения Земли или, что то же самое, длина земного шара. средний солнечный день, не является постоянным. Уильям Феррел в 1864 году и Шарль-Эжен Делоне в 1865 году предсказал, что вращение Земли замедляется приливами. Это можно было проверить наблюдениями только в 1920-х годах с очень точной Часы Shortt-Synchronome и позже, в 1930-х годах, когда кварцевые часы начали заменять маятниковые часы в качестве эталонов времени (Маккарти и Зайдельманн, 2009 г., гл. 9).
Шкалы времени и календарь
Видимое солнечное время время обозначено солнечные часы, и определяется видимым движением Солнца, вызванным вращением Земли вокруг своей оси, а также вращением Земли вокруг Солнца. Среднее солнечное время с поправкой на периодические изменения видимой скорости Солнца при вращении Земли по своей орбите. Самая важная из таких шкал времени Всемирное время, что является средним солнечным временем при 0 градусах долгота (в Гринвичский меридиан). Гражданское время основан на UT (фактически универсальное глобальное время), а гражданские календари считают средними солнечными днями.
Однако вращение самой Земли нерегулярно и замедляется по отношению к более стабильным индикаторам времени: в частности, движению планет и атомным часам.
Как следствие, тропический год, следующий за сезонами на Земле, считая в солнечных днях UT, все больше не совпадает с выражениями для равноденствий в эфемеридах в TT.
Как поясняется ниже, долгосрочные оценки продолжительности тропического года использовались в связи с реформой Юлианский календарь, в результате чего появился григорианский календарь. Участники той реформы не знали о неравномерном вращении Земли, но теперь это можно в какой-то степени учесть. В таблице ниже приведены Моррисон и Стивенсон (S&M) 2004 г. оценки и стандартные ошибки (σ) для ΔT в даты, важные в процессе разработки григорианского календаря.
| Мероприятие | Год | Ближайший год S&M | ΔТ | σ |
|---|---|---|---|---|
| Начало юлианского календаря | −44 | 0 | 2ч56м20с | 4 мин. 20 сек. |
| Первый Никейский собор | 325 | 300 | 2ч8м | 2м |
| Начало григорианского календаря | 1582 | 1600 | 2м | 20 с |
| экстраполяция с низкой точностью | 4000 | 4ч13м | ||
| экстраполяция с низкой точностью | 10,000 | 2d11h |
Экстраполяции с низкой точностью вычисляются с выражением, предоставленным Моррисон и Стивенсон (2004)
ΔТ в секундах = −20 + 32т 2
куда т измеряется в юлианских веках с 1820 года. Экстраполяция приведена только для того, чтобы показать ΔТ нельзя пренебречь при оценке календаря на длительные периоды; Борковский (1991, п. 126) предупреждает, что «многие исследователи пытались подогнать параболу к измеренному ΔТ значений для определения величины замедления вращения Земли. Результаты, взятые вместе, довольно обескураживают «.
Продолжительность тропического года
Средний промежуток времени между равноденствиями
Прежде чем рассматривать пример, равноденствие необходимо изучить. В расчетах солнечной системы есть две важные плоскости: эклиптика (орбита Земли вокруг Солнца), а плоскость небесный экватор (Экватор Земли в проекции в космос). Эти две плоскости пересекаются по линии. Один направление указывает на так называемые весеннее, северное или мартовское равноденствие которому присвоен символ ♈︎ (этот символ выглядит как рога баран потому что раньше он был в направлении созвездия Овен). Противоположный направление дается символ ♎︎ (потому что раньше он был Весы). Из-за прецессия равноденствий и нутация эти направления меняются по сравнению с направлением далеких звезд и галактик, чьи направления не имеют измеримого движения из-за их большого расстояния (см. Международная небесная система отсчета).
При сравнении измерений тропических лет за несколько последовательных лет обнаруживаются вариации, которые связаны с возмущения Луной и планетами, действующими на Землю, и нутации. Meeus & Savoie (1992)., п. 41) приводил следующие примеры интервалов между мартовскими (северными) равноденствиями:
| дней | часы | мин | s | |
|---|---|---|---|---|
| 1985–1986 | 365 | 5 | 48 | 58 |
| 1986–1987 | 365 | 5 | 49 | 15 |
| 1987–1988 | 365 | 5 | 46 | 38 |
| 1988–1989 | 365 | 5 | 49 | 42 |
| 1989–1990 | 365 | 5 | 51 | 06 |
До начала 19-го века продолжительность тропического года определялась путем сравнения дат равноденствия, разделенных многими годами; этот подход дал иметь в виду тропический год (Meeus & Savoie 1992, п. 42).
Различные определения тропического года
Если выбрана другая начальная долгота Солнца, чем 0 ° (т.е. ♈︎), то время возврата Солнца к той же долготе будет другим. Это эффект второго порядка из-за того обстоятельства, что скорость Земли (и, наоборот, видимая скорость Солнца) изменяется по ее эллиптической орбите: быстрее в перигелий, медленнее в афелий. Теперь точка равноденствия движется относительно перигелия (и оба движутся относительно неподвижной звездной системы отсчета). От одного прохода равноденствия к другому Солнце совершает не совсем полную эллиптическую орбиту. Сэкономленное время зависит от того, где оно начинается на орбите. Если начальная точка близка к перигелию (например, декабрьское солнцестояние), то скорость выше средней, и видимое Солнце экономит мало времени, поскольку ему не нужно проходить полный круг: «тропический год» сравнительно длинный. Если начальная точка близка к афелию, то скорость ниже, а время, сэкономленное за счет того, что не нужно проходить ту же маленькую дугу, по которой прецессия равноденствия, больше: этот тропический год сравнительно короткий.
Следующие значения интервалов времени между равноденствиями и солнцестояниями предоставлены Meeus & Savoie (1992)., п. 42) for the years (лет) 0 и 2000. Это сглаженные значения, учитывающие эллиптическую форму орбиты Земли с использованием хорошо известных процедур (включая решение Уравнение Кеплера). Они не принимают во внимание периодические изменения, обусловленные такими факторами, как гравитационная сила вращающейся вокруг Луны и гравитационные силы других планет. Такие возмущения незначительны по сравнению с позиционной разницей, возникающей из-за того, что орбита является эллиптической, а не круговой.Meeus 2002, п. 362)
| Год 0 | 2000 год | |
|---|---|---|
| Между двумя Северные равноденствия | 365.242 137 дней | 365.242 374 дней |
| Между двумя Северное солнцестояние | 365.241 726 | 365.241 626 |
| Между двумя Южное равноденствие | 365.242 496 | 365.242 018 |
| Между двумя Южные солнцестояния | 365.242 883 | 365.242 740 |
| Средний тропический год (Выражение лица Ласкара) | 365.242 310 | 365.242 189 |
Текущее значение среднего тропического года
Средний тропический год на 1 января 2000 г. был 365.242 189 7 или 365 эфемеридные дни, 5 часов, 48 минут, 45,19 секунды. Это медленно меняется; выражение, подходящее для расчета продолжительности тропического года в эфемеридных днях, между 8000 г. до н.э. и 12000 г. н.э.
Современные астрономы определяют тропический год как время, когда средняя долгота Солнца увеличивается на 360 °. Процесс поиска выражения для продолжительности тропического года состоит в том, чтобы сначала найти выражение для средней долготы Солнца (относительно), такое как выражение Ньюкомба, данное выше, или выражение Ласкара (1986, п. 64). Если смотреть на период в один год, средняя долгота почти линейно зависит от земного времени. Чтобы найти продолжительность тропического года, средняя долгота дифференцируется, чтобы получить угловую скорость Солнца как функцию земного времени, и эта угловая скорость используется для вычисления того, сколько времени потребуется Солнцу, чтобы переместиться на 360 °. (Meeus & Savoie 1992, п. 42; Астрономический альманах за 2011 год, L8).
Приведенные выше формулы дают продолжительность тропического года в эфемеридных днях (равных 86400 секунд СИ), а не солнечные дни. Именно количество солнечных дней в тропическом году важно для синхронизации календаря с временами года (см. Ниже).
Календарный год
В Григорианский календарь, используемый в гражданских и научных целях, является международным стандартом. Это солнечный календарь, который предназначен для поддержания синхронизации со средним тропическим годом (Добжицкий 1983, п. 123). Его цикл составляет 400 лет (146 097 дней). В каждом цикле повторяются месяцы, даты и дни недели. Средняя продолжительность года составляет 146097/400 = 365 97 ⁄400 = 365,2425 дней в году, что близко к среднему тропическому году в 365,2422 дня (Зайдельманн 1992, стр. 576–81).
Если общество в будущем по-прежнему придает значение синхронизации между гражданским календарем и временами года, в конечном итоге потребуется еще одна реформа календаря. Согласно Блэкберну и Холфорду-Стревенсу (которые использовали значение Ньюкомба для тропического года), если тропический год останется на уровне 1900 г. 365.242 198 781 25 дней по григорианскому календарю будет на 3 дня, 17 минут, 33 секунды от Солнца после 10 000 лет. Эта ошибка усугубляется тем, что продолжительность тропического года (измеренная в земном времени) сокращается примерно на 0,53 с за столетие. Кроме того, средний солнечный день удлиняется примерно на 1,5 мс за столетие. Эти эффекты приведут к тому, что календарь отстает почти на день от 3200. Количество солнечных дней в «тропическом тысячелетии» уменьшается примерно на 0,06 на тысячелетие (без учета колебательных изменений реальной длины тропического года). [2] Это означает, что со временем должно быть все меньше и меньше високосных дней. Возможной реформой было бы опустить високосный день в 3200, оставить 3600 и 4000 в качестве високосных, а затем сделать все столетние года общими, кроме 4500, 5000, 5500, 6000 и т. Д. ΔT недостаточно предсказуем, чтобы формировать более точные предложения (Блэкберн и Холфорд-Стревенс 2003, п. 692).