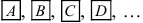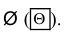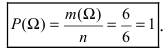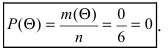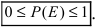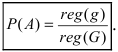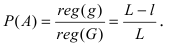Что называют случайными массовыми событиями приведите примеры
Большая Энциклопедия Нефти и Газа
Массовые случайные события
Массовые случайные события обладают свойством устойчивости, частоты: наблюдаем. [1]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах. [2]
Массовые случайные события следует отличать от единичных, исключительных, обладающих той особенностью, что опыт, с которым связаны эти события, принципиально невоспроизводим. Например, событие 1 мая 1975 года в Москве шел дождь является в этом смысле исключительным, так как воспроизвести наступление указанного дня невозможно. В то же время событие 1 мая в Москве шел дождь ( без упоминания о годе) является, несомненно, массовым: ведь наблюдать погоду в Москве 1 мая можно в течение многих лет. [3]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах. [4]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах и стремятся ( по вероятности) к некоторому постоянному числу. [5]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах и стремятся ( по вероятности) к некоторому, постоянному числу. [6]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах и стремятся ( по вероятности) к некоторому постоянному числу. [7]
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний ( с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах. [8]
Содержание:
Основные понятия теории вероятностей:
1. Предмет теории вероятностей.
Определение: Случайным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти.
Например, при подбрасывании монеты нельзя угадать заранее, что выпадет: “решка” (аверс) или “орел” (реверс). Каждое из этих событий является простым и не может быть выражено через более простые события.
Определение: Элементарным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти, а также не может быть представлено посредством более простых событий.
В теории вероятностей случайные элементарные события принято обозначать заглавными начальными буквами латинского алфавита
Определение: Сложным случайным событием называется событие, которое состоит из осуществления двух или более элементарных событий.
Определение: Достоверным событием называется такое событие, которое обязательно произойдет в рамках данного опыта. Достоверное событие обозначается
Определение: Невозможным событием называется такое событие, которое ни при каких условиях не может произойти.
Невозможное событие обозначается
Например, совокупность выигрыша, проигрыша и ничья в шахматной партии образуют достоверное совокупное событие, т.е. одно из этих событий обязательно произойдет при игре в шахматы. При бросании кубика выпадение грани с 7 очками является невозможным событием.
Определение: Совместными событиями называются события, которые могут одновременно произойти в рамках данного опыта, все другие события называются несовместными.
Например, при бросании кубика выпадение грани с 4 очками (событие А) и выпадение четной грани (событие В) являются совместными событиями, а выпадение грани с 3 очками (событие А) и выпадение четной грани (событие В) являются несовместными событиями.
Определение: Полной группой случайных событий называется совокупность таких несовместных событий, что в результате проведения эксперимента хотя бы одно из них обязательно произойдет.
Замечание: Если в словесном описании случайного события присутствуют слова “хотя бы один”, то такое событие противоположно событию, содержащему в своем словесном описании слова “ни один”.
Определение: Равновозможными событиями называются такие случайные события, которые в условиях эксперимента имеют объективно равные шансы не произойти или произойти.
Например, однородность материала кости и несмещенность центра тяжести кубика являются теми условиями, при которых объективно возможно выпадение любой грани кубика.
Способы определения вероятности событий
Существуют два способа определения вероятности события
Классическое определение вероятности
Определение: Вероятностью события называется численная мера степени объективной возможности случайного события.
Классическое определение вероятности применяется для нахождения вероятности конечного числа несовместных и равновозможных событии, образующих полную группу.
Пример №1
Пусть в урне находится 6 шаров: 1 белый, 2 красных и 3 синих. Опыт состоит в том, что из урны наудачу извлекают один шар. Определить полную группу случайных событий и наиболее вероятное событие.
Решение:
Классическое определение вероятности состоит в следующем:
Определение: Вероятностью случайного элементарного события называется отношение числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу.
В силу того,что события А, В и С образуют достоверное совокупное событие, то 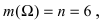
Если в рассматриваемом Примере. обозначить через D событие, состоящее в том, что из урны извлекают черный шар, то этому событию благоприятствует нуль исходов (m(D) = 0), так как в урне нет черных шаров. Следовательно, событие D является невозможным событием О, а его вероятность равна:
Из рассмотренного Примере. видно, что вероятности всех событий есть положительные величины, которые принимают значения между вероятностью невозможного (0) и вероятностью достоверного (1) событий, т.е.
Замечание: Вероятность любого случайного события есть безразмерная и положительная величина, принимающая значения из промежутка от 0 до 1. Чем ближе вероятность события к нулю, тем меньше его возможность появления в данном опыте. Чем ближе вероятность события к единице, тем выше его возможность появления в данном эксперименте.
Геометрический способ определения вероятности
Геометрическое определение вероятности применяется для вычисления вероятности бесконечного числа несовместных и равновозможных событий, образующих полную группу.
Пусть имеется некоторая область G, которая может быть представлена в виде линии, площади или объема. Внутри области G находится другая область g, внутрь которой должна попасть точка, наудачу брошенная в область G. Пусть событие А состоит в том, что при попадании в область g включается лампочка, а при попадании в область G лампочка не загорается. Обозначим размеры областей g и G через 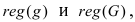
Пример №2
Пусть на нити длиной L подвешен груз. Определить вероятность разрыва нити в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l.
Решение:
Пусть событие А состоит в том, что нить разорвется в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l. Появлению этого события благоприятствуют все точки нити длиной L-l, т.е. 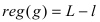
Статистический способ определения вероятности событий
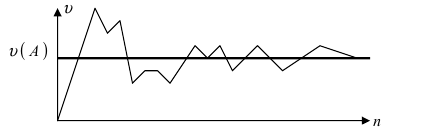
Данный способ определения вероятности событий применяется тогда, когда неприменимы два вышеприведенных способа. В основу данного способа положена устойчивость частоты появления изучаемого события при достаточно большом числе проводимых опытов, т.е. P(A) = v(A). При небольшом числе испытаний частота носит случайный характер, но при 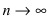
Рис. 1. Стабилизация частоты появления случайного события при
Косвенный способ определения вероятности событий
Данный способ определения вероятности событий применяется тогда, когда неприменимы три вышеприведенных способа. Он основан на теоремах теории вероятностей, которые рассматриваются ниже.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Теория вероятностей, формулы и примеры
Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.
Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.
Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».
Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.
Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.
Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:
Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.
Формулы по теории вероятности
Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.
Случайные события. Основные формулы комбинаторики
Классическое определение вероятности
Вероятностью события A в некотором испытании называют отношение:
P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A
Таким образом, вероятность любого события удовлетворяет двойному неравенству:
Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?
Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:
Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.
Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?
Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).
Геометрическое определение вероятности
Геометрическая вероятность события А определяется отношением:
P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно
Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.
Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?
У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!
Сложение и умножение вероятностей
Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B)
Эта теорема справедлива для любого числа несовместных событий:
Если случайные события A1, A2. An образуют полную группу несовместных событий, то справедливо равенство:
Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:
P(A + B) = P(A) + P(B) − P(AB)
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:
P(AB) = P(A) * P(B)
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.
Найдем вероятности того, что формула содержится:
А — формула содержится в первом справочнике;
В — формула содержится во втором справочнике;
С — формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.
Формула полной вероятности и формула Байеса
 |
По теореме умножения вероятностей:
Аналогично, для остальных гипотез:
Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.
Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Формула Бернулли
При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.
Биномиальное распределение — распределение числа успехов (появлений события).
Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.
Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:
Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂
Наивероятнейшее число успехов
Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:
Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.
В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:
 |
Здесь λ = np обозначает среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.
События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).
При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.
Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
P1000(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.
Ответ: ориентировочно 0,18.
Теоремы Муавра-Лапласа
Кроме того, пусть Pn(k1;k2) — вероятность того, что число появлений события А находится между k1 и k2.
Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то
Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:
Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.
Тема 8: ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ СИГНАЛОВ
Таковы первичные законы, установленные природой.
Вергилий. Георгики. (Римский поэт)
«Природа не злонамеренна, но коварна». Это не закон. Это только следствие теории вероятностей. И все же непонятно, почему единственная муха в ресторане падает именно в мой суп.
Владимир Бакаев. Наблюдения. (Уральский геофизик)
Содержание: 8.1. Основные понятия теории вероятностей. События и явления. Классификация случайных событий. Сумма событий. Произведение событий. Полная группа событий. Сложные события. 8.2. Вероятности случайных событий. Частотное определение. Определение на основе меры. Основные положения теории вероятностей. Сложение вероятностей. Условная вероятность. Умножение вероятностей. Независимость событий. Формула полной вероятности. Формула Байеса. 8.3. Случайные величины. Общие понятия. Вероятности случайных величин. Функции от случайной величины. Моменты распределения. Основные числовые характеристики случайных величин. Некоторые распределения случайных величин. Характеристическая функция. 8.4. Системы случайных величин. Функция распределения вероятностей системы. Плотность вероятностей системы. Условные законы распределения. Функции регрессии. Статистическая независимость случайных величин. Моменты систем случайных величин. Сумма и разность случайных величин. Литература.
8.1. Основные понятия теории вероятностей [л28,л29].
События и явления.Все события и явления реального мира разделяются на закономерные (детерминированные) и случайные (вероятностные).
Случайность событий может быть обусловлена как собственной физической природой явлений, что характерно для большинства физических процессов в микромире (например, распад радиоактивных ядер), так и определенным вероятностным характером реализации явлений в силу их многофакторной и, как правило, нелинейной зависимости от внешних и внутренних условий, что характерно для процессов в макромире. Например, индивидуализация исхода бросания игральной кости начинается с вариации некоторых начальных условий (положение в пространстве, скорость и направление движения, момент инерции, момент вращения и пр.) и продолжается на всем пути движения кости вплоть до остановки (трение о воздух, положение в момент удара о стол, поглощение энергии удара и пр.). Невозможность точного повторения всех условий опыта определяет случайность результата.
С практической точки зрения явление или процесс считаются случайными, если в их формировании в той или иной форме присутствует неопределенность и невозможно с заданной точностью предсказать результаты их конкретных реализаций, физического отображения и измерения в ходе контролируемых экспериментов или повторить в ходе многократных реализаций.
Два события называются совместными, если появление одного из них не влияет и не исключает появление другого. Совместные события могут реализоваться одновременно, как, например, появление какого-либо числа на одной кости ни коим образом не влияет на появление чисел на другой кости. События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).
Попутно заметим, что для логических операций имеем: А+А=А и А×А=А.
D = A×B×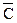
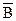
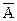
8.2. Вероятности случайных событий [л30,л28,л29].
Предсказание конкретной реализации случайных событий невозможно. Однако интуитивная ориентировка в случайных событиях известна каждому. Если при игре в кости дважды выпали две шестерки, то едва ли кто-нибудь в третий раз поставит на 12 очков. Это определяется тем, что и случайные события подчиняются определенным вероятностным закономерностям и при повторениях испытаний предсказуемы «в среднем».
Понятие вероятности событий относится к фундаментальным понятиям теории вероятностей. Вероятность случайного события является количественной мерой степени объективной возможности появления этого события в единичном опыте (в единичной реализации случайного явления). На протяжении последних трех веков достаточно интенсивного развития теории вероятностей многие ученые делали попытки сформулировать это фундаментальное понятие на основе строгой логики. Приведем только два из них.
Частотное определение. При N реализациях некоторого случайного явления случайное событие А наблюдалось n раз. Если случайные события в этом явлении взаимно независимы, несовместны и составляют полную группу, то вероятность события А определяется выражением:
P(A) = 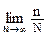
Так как диапазон значений n в данном выражении ограничен интервалом 0 £ n £ N, то отсюда следует, что значения вероятностей событий заключены в интервале от 0 до 1.
Пример.В урне находятся 5 белых и 7 черных шаров. Какова вероятность извлечь из урны 3 белых шара?
Общее число возможных способов извлечь 3 шара из 12 равно числу сочетаний из 12 по 3:
Число возможных сочетаний из 5 белых шаров по 3: n = 5!/(3!×2!) = 10.
Искомая вероятность: P = n/N = 10/220.
При практических оценках вероятностей значение (n/N) называют относительной частотой (или частностью) данного события в данной серии наблюдений. Относительная частота событий при многократных наблюдениях является достаточно устойчивой величиной, флюктуирующей в окрестностях вероятности данных событий, причем величина флюктуаций тем меньше, чем больше количество наблюдений.
Определение на основе меры. Введем пространство (множество) W, элементы которого wi являются случайными элементарными событиями, т.е. W =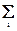
1. P(W) = 1, т.е. вероятность появления события, принадлежащего к данному пространству (wi Î W), равна 1 (условие нормировки меры).
2. Если подмножества элементарных событий А Î W и В Î W, каждое из которых принадлежит данному пространству W, не имеют общих элементов, то Р(А+В) = Р(А) + Р(В), т.е. вероятность того, что наблюдаемое событие принадлежит либо подмножеству А, либо подмножеству В, равна сумме вероятностей наблюдать это событие отдельно в подмножествах А и В.
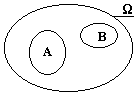 Рис. 8.2.1. Рис. 8.2.1. |
Для иллюстрации различных положений теории вероятностей удобно использовать условные графические отображения пространств случайных событий, пример которых приведен на рис. 8.2.1. Полное пространство W элементарных событий wi ограничивается произвольным контуром, площадь которого принимается равной 1 и равна вероятности появления событий wi в пространстве W, при этом полагается, что события wi равномерно заполняют пространство W. Группы событий w Î A или w Î В отображаются соответственно замкнутыми контурами внутри пространства W с площадями, равными вероятностям событий А и В.
Основные положения теории вероятностей вытекают непосредственно из определения понятия вероятности.
1. Вероятность любого случайного события А является неотрицательной величиной, значение которой заключено в интервале от 0 до 1.
2. Вероятность достоверного события равна 1.
В общем случае событие W представляет собой сумму полной группы возможных элементарных событий данного случайного явления: W =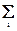
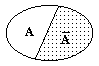 Рис. 8.2.2. Рис. 8.2.2. |
Сумма противоположных событий тоже составляет полную группу событий и соответственно вероятность суммы противоположных событий равна 1 (рис. 8.2.2):
P(A+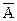
Примером может служить бросание горсти монет. Орел или решка для каждой монеты – противоположные события. Сумма событий для горсти в целом равна 1 независимо от соотношения выпавших орлов и решек.
3. Вероятность невозможного события равна 0.
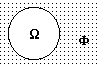 Рис. 8.2.3. Рис. 8.2.3. |
Сложение вероятностей зависит от совместности и несовместности событий.
Несовместные события. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий. Это вытекает из того, что множество С = А+В включает подмножества А и В, не имеющие общих точек, и Р(А+В) = Р(А)+Р(В) по определению вероятности на основе меры. По частотному определению вероятности в силу несовместности событий имеем:
P(A+B) = 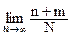
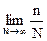
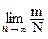
Противоположные события также являются несовместными и образуют полную группу. Отсюда, с учетом (8.2.3):
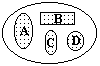 Рис. 8.2.4. Рис. 8.2.4. |
В общем случае для группы несовместных событий (рис. 8.2.4):
если все подмножества принадлежат одному множеству событий и не имеют общих точек (попарно несовместны). А если эти подмножества образуют полную группу событий, то с учетом (8.2.2):
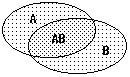 Рис. 8.2.5. Рис. 8.2.5. |
Совместные события. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления (рис. 8.2.5):
Разобьем события А и В каждое на два множества, не имеющие общих точек: А’, A» и B’, B». Во множества А» и B» выделим события, появляющиеся одновременно, и объединим эти множества в одно множество С. Для этих множеств действительны выражения:
С = A»×B» º А» º В» º А×В, P(C) = P(A») = P(B») = P(A×B).
Множества A’, B’ и С не имеют общих точек и можно записать:
P(A+B) = P(A’+B’+C) = P(A’) + P(B’) + P(С).
Подставляя в правую часть этого уравнения вышеприведенные выражения, приходим к выражению (8.2.8). Физическая сущность выражения достаточно очевидна: суммируются вероятности событий А и В и вычитаются вероятности совпадающих событий, которые при суммировании сосчитаны дважды.
Пример.Вытащим одну карту из колоды (52 карты). Какова вероятность того, что карта окажется или тузом, или пиковой мастью?
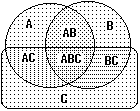 Рис. 8.2.6. Рис. 8.2.6. |
На рис. 8.2.6 на примере трех пространств можно видеть причины появления в выражении (8.2.9) дополнительных сумм вероятностей совпадающих пространств и их знакопеременности. При суммировании вероятностей пространств А,В и С, имеющих общее пространство АВС, его вероятность суммируется трижды, а при вычитании вероятностей перекрывающихся подпространств АВ, АС и ВС трижды вычитается (т.е. обнуляется), и восстанавливается дополнительным суммированием с вероятностью пространства АВС.
Второй сомножитель выражения (8.2.10) из общего числа случаев n1 события А определяет долю, когда одновременно происходит и событие В, т.е. вероятность события В при условии, что произошло событие А. Эта вероятность называется условной вероятностью события В по событию А и записывается в виде Р(В/А):
Р(А) = 13/52. Карта не возвращается в колоду, следовательно, Р(В/А) = (13-1)/(52-1).
В общем случае может определяться условная вероятность события В в предположении, что произошли события А1, А2 и др.: Р(В/А1,А2. ).
Для условной вероятности событий B по событиям A применяется также обозначение РA(B).
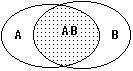 Рис. 8.2.7. Рис. 8.2.7. |
Умножение вероятностей совместных событий. Формула определения вероятности события А×В (А и В одновременно, рис. 8.2.7), которую обычно называют формулой умножения вероятностей, непосредственно следует из выражения (8.2.11):
Р(А) = 13/52. Р(В/А) = (13-1)/(52-1). Р(АВ) = (13×12)/(52×51) @ 0.0588
В общем случае, вероятность умножения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других:
Независимость событий. Если появление событий А не изменяет вероятности появления событий В, равно как и появление событий В не изменяет вероятности событий А, то события А и В считаются независимыми. Для таких событий Р(А/В) = Р(А), Р(В/А) = Р(В) и Р(А×В) = Р(А)×Р(В).
Р(А) = 4/52. Р(В) = 13/52. Р(АВ) = 1/52. Р(АВ) = Р(А)Р(В) = (4/52)(13/52) = 1/52.
События А и В независимы.
Подмножества, образованные из независимых событий, также являются независимыми. Если условие (8.2.13) не выполняется, но выполняется для каждой пары событий из этой группы (А×В, А×С, В×С и пр.), то такие события называются попарно независимыми.
Если события Аi образуют разбиение пространства событий и все P(Ai) > 0, то для любого события В имеет место формула полной вероятности:
P(B) =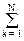
что непосредственно следует из (8.2.14) для попарно несовместных событий:
Р(А) = M/N. Р(

Отсюда: Р(В) = Р(А)Р(В/А) + Р(

Этот результат давно известен и применяется, например, при жеребьевке, определяя независимость результатов жеребьевки от порядка ее участников при вынимании шаров.
Формула Байеса(или формула гипотез). Если для пространства событий Ai выполнено условие (8.2.14) и для произвольного события В имеет место формула полной вероятности (8.2.15), то одновременно для любой комбинации событий В и Аk имеет место и формула умножения вероятностей (8.2.12)
из которой следует:
Заменяя в этом уравнении выражение Р(В) формулой полной вероятности (8.2.15), получаем формулу Байеса:
Р(Аk/В) =Р(Аk)×Р(В/Аk) /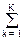
Нетрудно видеть, что знаменатель функции является нормировочным коэффициентом приведения суммы вероятностей к 1:
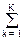
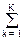
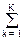
Пример.В одном районе «дикого» туризма прогнозирование количества А несчастных случаев на следующие сутки проводилось по следующей методике (для наглядности рассмотрим пример на конкретных условных данных).
Априорные вероятности P(Аk) несчастных случаев на текущий день, вычисленные по предыдущему дню: P(А1=0) = 0.2, P(А2=1) = 0.4, P(А3=2) = 0.3, P(А4=3) = 0.1.
За текущий день зарегистрировано 0 несчастных случаев (В = 0).
Условные вероятности P(B/Ak) вычислялись по формуле плотности распределения вероятностей редких событий (формула Пуассона): P(B/Ak) = (Ak) B ×exp(-Ak) /B!
P(0/0) = 1, P(0/1) = 0.368, P(0/2) = 0.135, P(0/3) = 0.05.
Нормировочный делитель формулы Байеса: 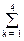
Апостериорные вероятности P'(Ak) = P(Ak/B) = P(Ak/0) несчастных событий на следующий день:
Проверка: 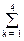
8.3. Случайные величины [л30,л31,л2,л4,л15].
Общие понятия. Под случайной величиной в узком смысле данного термина можно понимать числовое отображение исхода случайного явления или опыта, если в основе его формирования лежат определенные физические процессы, вероятностные по свое природе. Так, например, число гамма-квантов, зарегистрированных радиометром за произвольный временной интервал от радиоактивной пробы, является случайной величиной как в силу вероятностной природы самого радиоактивного распада, так и в силу вероятностного характера их распространения, рассеяния и поглощения в окружающей среде и в детекторе радиометра.
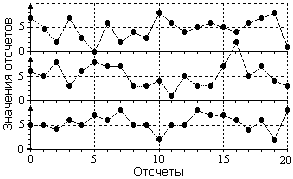 Рис. 8.3.1. Рис. 8.3.1. |
Еще раз отметим, что отнесение тех или иных величин и отображающих их сигналов к случайным или неслучайным (детерминированным) в той или иной мере всегда относительно, особенно в геофизической практике. С одной стороны, ни в одной сколь угодно точно известной геологической обстановке нельзя исключить появления объекта или проявления какого-либо процесса, которые совершенно непредсказуемым образом могут повлиять на распределение информационного сигнала. С другой стороны можно отрицать и истинную случайность физических явлений и процессов, поскольку по мере накопления информации появляется возможность их описания все более точными математическими формулами детерминированного действия.
Множество возможных значений случайной величины принято называть пространством (множеством) состояний (генеральной совокупностью). Если пространство состояний образует континуум, то случайная величина является непрерывной. Если изменение состояний допускается для конечного (счетного) числа координат, то говорят о случайной непрерывной последовательности.
Случайную величину с конечным множеством состояний по непрерывной шкале координат называют дискретной, если она дискретна по множеству своих возможных значений. Если для случайного явления изменение состояний возможно только в конечном числе координат, то говорят о случайной дискретной последовательности. Для случайных явлений с дискретным множеством состояний статистические зависимости могут распространяться на ограниченное число k следующих друг за другом значений. Такие процессы называются марковскими k-го порядка.
p(x)dx = P(x 2 = а 2 sх 2
Моменты распределения.При решении многих практических задач нет особой необходимости в полной вероятностной характеристике каких-либо случайных величин, которую дает функция плотности распределения вероятностей. Очень часто приходится также иметь дело с анализом случайных величин, плотности вероятностей которых не отображаются аналитическими функциями либо вообще неизвестны. В этих случаях достаточно общее представление о характере и основных особенностях распределения случайных величин можно получить на основании усредненных числовых характеристик распределений.
Числовыми характеристиками случайных величин, которые однозначно определяются функциями распределения их вероятностей, являются моменты.
Начальные моменты n-го порядка случайной величины X (или просто моменты) представляют собой усредненные значения n-й степени случайной переменной:
mn º М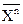
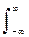
Соответственно, для случайных дискретных величин:
mn º М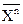
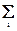
Центральные моменты n-го порядка, это моменты относительно центров распределения (средних значений) случайных величин:
mn º M<(X-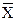
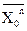
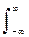
mn º M<(X-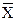
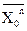
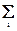
где 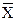
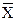
Связь между центральными и начальными моментами достаточно проста:
Соответственно, для случайных величин с нулевыми средними значениями начальные моменты равны центральным моментам.

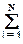
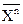
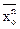
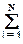

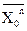
Погрешность оценок стремится к нулю при выборке N Þ ¥.
Среднее значение распределения является характеристикой сдвига значений случайных величин относительно x = 0 и представляет собой значение центра рассеяния случайных величин, т.е. математическое ожидание случайной величины по пространству возможных состояний:
M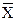
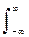
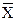
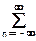
Если пространство возможных состояний случайных величин ограничено определенными конечными пределами, то соответственно интегрирование (или суммирование) осуществляется в этих пределах. В функциях от случайных величин постоянный множитель можно выносить за знак математического ожидания:
Оценка среднего значения по результатам N-выборки (выборочное среднее):

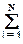
Значение 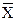


M<
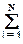
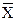
Отсюда следует, что выборочное среднее есть несмещенная оценка среднего значения генеральной совокупности, т.е. 
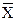
Дисперсия распределения характеризует размер пространства состояний случайной величины, величину их рассеивания по значениям относительно среднего значения:
D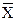
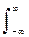
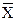
Оценка дисперсии по результатам N-выборки производится по формулам:
Dx = (1/N)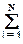

Для функции с×Х, где с = const, имеем:
Среднее квадратическое отклонение случайной величины от математического ожидания (среднего значения), равное корню квадратному из значения дисперсии:
sх = 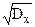
получило название стандарта (стандартного отклонения). Величину стандарта в относительных единицах среднего значения dx = s/mx называют вариацией или (в основном для временных процессов) флюктуацией значений случайной величины.
Пример.Плотность распределения случайных величин Х: p(x) = (a/2)exp(-a|x-b|), а=2, b=4.
Среднее значение и дисперсия: 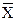
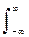
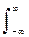
Среднее значение и дисперсия по выборке:

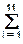
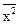
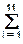
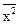

D(
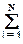
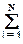
т.е. дисперсия средних значений 

s(
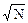
К числовым характеристикам случайных величин Х относятся также мода Мох, медиана Мех, асимметрия Sх и эксцесс Ех.
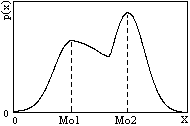 Рис. 8.3.5. Рис. 8.3.5. |
Мода распределения — это наиболее вероятное значение случайных величин, которому соответствует максимум плотности вероятностей. Функции плотности вероятностей могут иметь больше одного максимума. Такие распределения называют много- или полимодальными. На рис. 8.3.5 приведен пример двумодального распределения.
Для одномодальных распределений, симметричных относительно среднего значения, мода совпадает со средним значением, для асимметричных среднее значение обычно смещено относительно моды в сторону более длинного «хвоста» изменения плотности вероятностей.
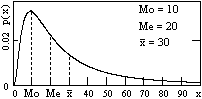 Рис. 8.3.6. Рис. 8.3.6. |
Понятие медианы обычно используется для непрерывных случайных величин.
В резко асимметричных распределениях случайных величин значения моды, медианы и среднего значения существенно расходятся, как, например, для логнормального распределения на рис. 8.3.6.
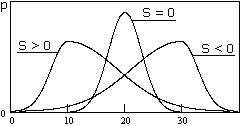 Рис. 8.3.7. Рис. 8.3.7. |
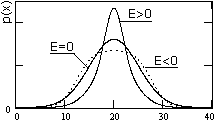 Рис. 8.3.8. Рис. 8.3.8. |
Эксцесс (или крутость) распределения случайных величин также безразмерное число:
Оценка числовых характеристик функций от случайных величин может производиться непосредственно по числовым характеристикам случайных величин с использованием правила переноса ошибок.
Допустим, что случайная величина Y является функционально зависимой от случайной величины Х и определяется выражением Y = g(x). Разложим это выражение в ряд Тейлора относительно математического ожидания 
Оценка математического ожидания 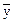
M





Отсюда, с точностью до членов второго порядка малости:
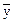

Оценка дисперсии распределения D(g(x)) = Dy:
Из формулы (8.3.11) имеем:
С использованием этого выражения в (8.3.13) с ограничением до 2-го порядка:
Dy » M<[(x-


sy = g'(

Для линейных функций g(x)
a×x+b выражения (8.3.12-14) являются точными.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет