Что называют периметром многоугольника 8 класс
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.
Периметр многоугольника
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
В математике периметр обозначают буквой P (пэ).
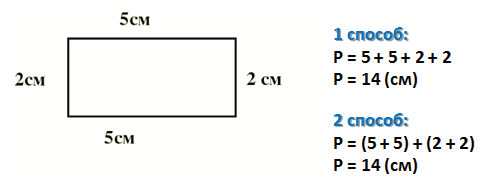
Периметр прямоугольника
Например, найдём периметр данного прямоугольника.
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
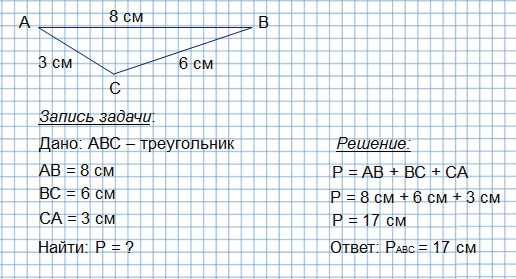
Периметр треугольника
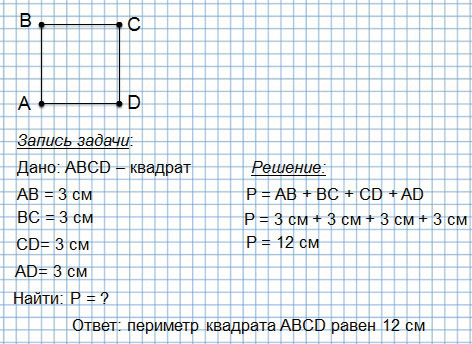
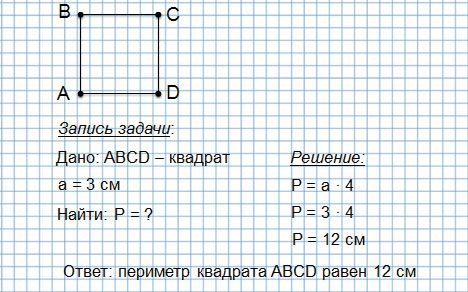
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Поделись с друзьями в социальных сетях:
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
    |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
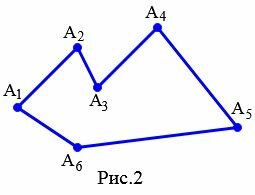 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
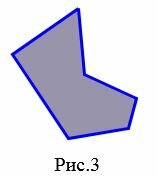 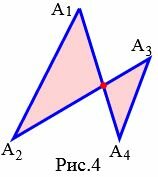 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
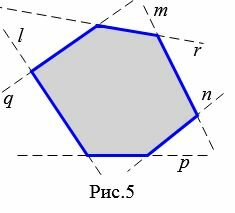 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
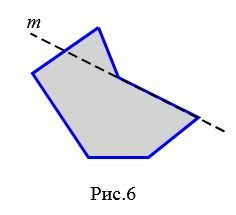 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
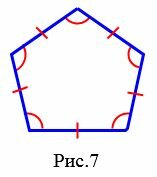 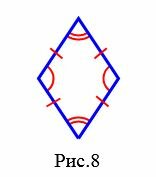 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
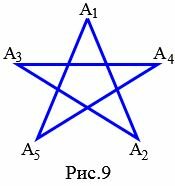 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
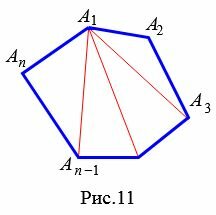 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Урок открытие новых знаний на тему : » Периметр многоугольника»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Конспект урока по “Математике» 2 «Б» класс
УМК: «Начальная школа 21 века»
Тема урока: «Периметр многоугольника»
Цель урока: организация совместной деятельности учащихся с целью знакомства с понятием «периметр многоугольника» и способами его вычисления.
помочь учащимся усвоить представления о периметре многоугольника и способах его нахождения, освоение данных понятий с целью применения их в жизненных ситуациях;
обеспечить усвоение знаний учащихся путём наблюдения и практической работы.
развивать речь учащихся, познавательную активность, умение следовать заданным вербальным инструкциям учителя;
совершенствовать мыслительные операции;
развивать психические процессы: память, мышление, воображение, внимание, эмоции;
развивать навык самооценки.
культуру поведения при фронтальной, групповой работе и работе в парах;
активности, усидчивости, прилежания в процессе учения.
Иметь представление о периметре; уметь находить периметр разными способами; уметь использовать математическую терминологию при составлении и чтении математических неравенств; находить значение выражений в два действия, используя знания правила порядка выполнения действий; устанавливать соответствия между изученными величинами.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; планировать своё действие в соответствии с поставленной задачей; высказывать своё предположение ( Регулятивные УУД).
Уметь выражать свои мысли в устной форме; слушать и понимать речь других ( Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).
Тип урока: урок формирования первоначальных предметных навыков, овладения предметными умениями.
Презентация, учебник, рабочая тетрадь,
интерактивная доска, компьютер, линейка, крандаш.
-Здравствуйте, ребята! Меня зовут Вероника Вадимовна и сегодняшний урок математики проведу у вас я.
— Крепко пожали друг другу руки и сказали “У нас сегодня все получится!”
Приветствуют учителя, внимательно слушают.
Личностные УУД: воспитание интереса занятием математикой, развитие мотивов учебной деятельности и формирование личностного смысла учения.
2.Актуализация опорных знаний
-сегодня у нас на уроке открытия новых знаний.Для начала мы проведем умственную зарядку.
(записываются только ответы)
— сумма чисел 15 и 15;
— сумма чисел 20 и 20;
— сумма чисел 30 и 30;
— сума чисел 60 и 10;
— разность чисел 50 и 25;
— разность чисел 45 и 5;
— разность чисел 50 и 10;
— разность чисел 30 и 15;
— разность чисел 100 и 90.
Детям предлагается поменяться тетрадями и осуществить взаимопроверку. Самоконтроль осуществляется с помощью слайда № 2
Личностные УУД: заинтересовать учащихся в приобретении расширений знаний и способов действий. Регулятивные УУД: проведение учениками самооценки, самоконтроля)
3.Подготовка к изучению новых знаний и способов действий.
Посмотри на экран (слайд № 4)
— Сколько четырёхугольников изображено на рисунке. Докажи свой ответ.
Раздаточный материал с изображением геометрических фигур. (слайд № 5)
— Какие фигуры изображены?
— Назовите, одним словом эти геометрические фигуры? (работа с раздаточным материалом)
— Дополните недостающие фигуры в вашей карточке. Объясните свой ответ.
Физминутка для глаз слайд
6 четырёхугольников; дети с помощью указки показывают эти четырёхугольники.
В первой лини – треугольник; в третьей линии – четырёхугольник.
Коммуникативные УУД: умение выражать свои мысли, учувствовать в учебном диалоге; работать в паре
Познавательные УУД: овладение логическими действиями анализа и сравнения.
Регулятивные УУД: Развивать способности к самоанализу и самоконтролю.
Личностные УУД: укрепляет здоровье младших школьников.
Знакомство с новым материалом:
— Сегодня на уроке мы будем продолжать работать с многоугольниками. Тему нашего урока вы мне сами назовёте, после решения задачи.
(чтение задачи учителем слайд № 6, раздаточный материал)
-Мы обозначили путь девочки отрезками,
какая геометрическая фигура получилась? Многоугольник (Четырёхугольник).
-Каждый отрезок имеет свою длину.
-Назовите мне длину каждого отрезка.
-Каким арифметическим действием мы найдём путь девочки?
-Мы с вами нашли сумму чего?
— А теперь открыли тетрали, пропустите 4 клетки вниз, запишите число 22 октября
Математики народ точный, поэтому они договорились обозначать периметр символом – латинской буквой Р.
— Запишем в своих тетрадях символ, которым обозначают периметр.
— Сделаем запись нахождения периметра.
— Помогите мне сформулировать тему нашего урока.
-Работа с дополнительным материалом (ответ ученика). Историческая справка.
— Ребята для чего нам в жизни необходимо умение вычислять периметр?
-кто знает, людям каких профессий необходимо знание о нахождении периметра?
— Мы с вами убедились, что знание о периметре необходимо нам в повседневной жизни. Поскольку мы находим периметр многоугольников разной величины (участок садовый, кусок ткани ит.д.), то и измеряется периметр в разных единицах измерения. Какие вы уже знаете?
Урок математики по теме «Периметр многоугольника»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Технологическая карта урока
Тема урока: «Периметр многоугольника»
Тип урока: урок «открытия» нового знания.
Цель урока: первичное усвоение новых знаний и способов действий при изучении темы: «Периметр многоугольника»
1. формировать умение решать задачи, связанные с нахождением периметра фигур,
2. формировать умение чертить геометрические фигуры.
1. Научатся распознавать изученные геометрические фигуры и называть их отличительные особенности;
2. находить периметр многоугольника разными способами.
1. Формировать умение определять учебную задачу, планировать свои достижения.
2. Формировать умения анализировать, классифицировать и видеть причинно-следственные связи, предлагать решение экологических проблем.
3.Формировать умение владеть диалогической формой речи, составлять рассказ по результатам.
-Учащиеся научатся определять учебную задачу.
-Учащиеся получат возможность научиться составлять план своих действий.
-Учащиеся научатся выявлять существенные признаки при анализе объектов и классифицировать их по группам.
-Учащиеся получат возможность научиться видеть причинно-следственные связи решения экологических задач (проблем).
-Учащиеся научатся владеть диалогической речью.
-Учащиеся получат возможность составлять рассказ по результатам.
1.Формировать учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи.
2.Формировать способность к самооценке на основе критериев успешности учебной деятельности.
1. учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи.
2. способность к самооценке на основе критериев успешности учебной деятельности.
Форма организации учебной деятельности: фронтальная, парная, индивидуальная.
Дидактические средства: учебник, раздаточный материал, презентация.
Интерактивное оборудование: компьютер, проектор.
Характеристика этапов урока
1.Мотивация к учебной деятельности.
Здравствуйте, ребята. Меня зовут Елена Александровна и сегодня я проведу у вас урок математики. Проверьте свою готовность к уроку: у вас на партах должен лежать учебник, тетрадь, карточки для самостоятельной работы и пенал.
Урок я хочу начать с цитаты М. В. Ломоносова: «Математику уже затем учить надо, что она ум в порядок приводит».
-Ребята, как вы понимаете это высказывание?
Приветствуют учителя. Проверяют готовность к уроку.
Р: осуществлять волевую саморегуляцию
К: Учащиеся получат возможность научиться учитывать разные мнения и интересы и обосновывать собственную позицию.
У учащихся будет сформирован интерес к изучению предмета.
2. Актуализация и фиксирование индивидуального затруднения в пробном действии.
-Ребята, отгадайте загадки и скажите, о каких геометрических фигурах идёт речь:
1.Хоть сто лет по ней идти,
Не найти конца пути. У какой фигуры нет начала и конца?
2.Часть прямой, ограниченная с двух сторон точками.
3. Об этой фигуре разносится весть: конца в ней пусть и нет, начало – то есть.
4. Он давно знаком со мной.
Каждый угол в нем прямой.
Все четыре стороны
Вам его представить рад,
5. Три угла, три стороны,
Могут разной быть длины.
-Ребята, посмотрите на доску, а как называется эта геометрическая фигура?
Она замкнутая или не замкнутая?
А как узнать длину ломаной линии?
А теперь давайте превратим эту не замкнутую ломаную линию в замкнутую. Какая фигура у нас получилась?
-А сейчас нам нужно украсить этот четырёхугольник ленточной, но как же мы узнаем, какой длины лента нам понадобится?
-Ребята, посмотрите на слайд. Каким одним словом можно назвать представленные фигуры?
-Назовите, какой многоугольник имеет меньше всего сторон, углов?
Сложить длины звеньев.
Нужно измерить каждую сторону и сложить.
К: Учащиеся научатся владеть диалогической речью
У учащихся будет сформирован интерес к изучению предмета.
-Ребята, откройте учебник на странице 42 и назовите тему нашего урока.
-Прочитайте то, что написано под темой.
Да, это цель нашего урока.
-Узнать, что называют периметром многоугольника и научиться его находить.
Р: Учащиеся научатся определять учебную задачу.
У учащихся будет сформирован интерес к изучению предмета.
4. Построение проекта выхода из затруднения.
-Ребята, какие задачи мы поставим на этот урок?
Молодцы, это и будет нашим планом действий на урок.
1.Узнать, что называют периметром многоугольника.
2.Научимся находить периметр многоугольника.
3.Научимся решать задачи для нахождения периметра многоугольника.
Р: Научатся принимать и сохранять учебную задачу.
У учащихся будет сформирован интерес к изучению предмета.
5.Реализация построенного проекта.
Откройте тетради, запишите число.
-Ребята, давайте узнаем, что же такое периметр многоугольника?
Периметр с латинского переводится как «обойти вокруг».
Прочитайте правило, данное в учебнике.
-Давайте попробуем найти периметр фигур, данных в учебнике над правилом. Возьмите линейку и найдите периметр этих многоугольников.
1 ряд ищет периметр 1 фигуры, 2 – 2, 3 – 3.
Что у вас получилось?
-Прочитайте задание 1 под цифрой 2. Как можно найти периметр многоугольника, не узнавая длину каждой стороны с помощью циркуля? Найдите длину многоугольника с помощью циркуля, задание выполняем также по рядам.
К: Учащиеся получат возможность научиться учитывать разные мнения и интересы и обосновывать собственную позицию
У учащихся будет сформирован интерес к изучению предмета.
6. Первичное закрепление с проговариванием во внешней речи
Выполним задание номер 2. Прочитайте условие задачи.
Давайте изобразим этот треугольник. Подпишите длину каждой стороны. Теперь нам нужно найти периметр этого треугольника.
Запишите выражение в тетрадь.
Какое выражение и какой ответ у вас получились?
Какой длины была проволока у Славы изначально?
К: Учащиеся научатся владеть диалогической речью
У учащихся будет сформирован интерес к изучению предмета.
7.Самостоятельная работа с самопроверкой по эталону.
Сейчас возьмите карточки для самостоятельной работы, которые лежат у вас на партах. Подпишите их. Выполните задания.
Поменяйтесь карточками с соседом по парте и, сверяясь с доской, проверьте работы друг друга. Поставьте оценку.
Если всё правильно – оценка 5.
Если есть 1 ошибка – оценка 4.
Если все задания выполнены не верно – оценка 2.
Хорошо, с последних парт на 1 передайте карточки.
Р: осуществлять волевую саморегуляцию
У учащихся будет сформирован интерес к изучению предмета.
8.Включение в систему знаний и повторение
-Ребята, какую тему мы сегодня прошли?
-Что такое периметр многоугольника?
-Как находить периметр многоугольника?
-Какие трудности у вас возникали на уроке?
К: Учащиеся научатся владеть диалогической речью
У учащихся будет сформирован интерес к изучению предмета.
9. Рефлексия учебной деятельности на уроке.
Ребята, наш урок подошёл к концу.
Возьмите маленькие карточки с лесенкой. Нарисуйте смайлик на 1 ступеньке, если вы считаете, что на уроке вы работали хорошо, было интересно, и вы узнали что-то новое.
На 2 ступеньке, если на уроке вам было интересно, вы принимали активное участие, но было сложно.
И на 3 ступеньке, если было сложно и вы ничего не поняли.
Спасибо за урок. До свидания.
К: Учащиеся научатся владеть диалогической речью
У учащихся будет сформирован интерес к изучению предмета.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
4 класс математика «Диаграммы»
4 класс математика «Сравнение многозначных чисел»
1 класс математика «Знаки > (больше),
Контрольная работа «Показательные уравнения и неравенства» (10 класс)
Презентация по математике «Умножение и деление дробей»(6 класс)
«Сборник комплексных диагностических работ по математике для проверки знаний начало учебного года»
Причины неуспеваемости и пути их преодоления
Технологическая карта фрагмента урока математики по теме: «Прямоугольник»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5383849 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Время чтения: 2 минуты
МГУ откроет первую в России магистерскую программу по биоэтике
Время чтения: 2 минуты
Апробацию новых учебников по ОБЖ завершат к середине 2022 года
Время чтения: 1 минута
Школьники из Москвы выступят на Международной олимпиаде мегаполисов
Время чтения: 3 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.