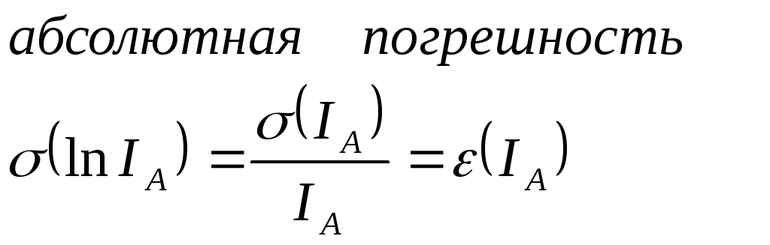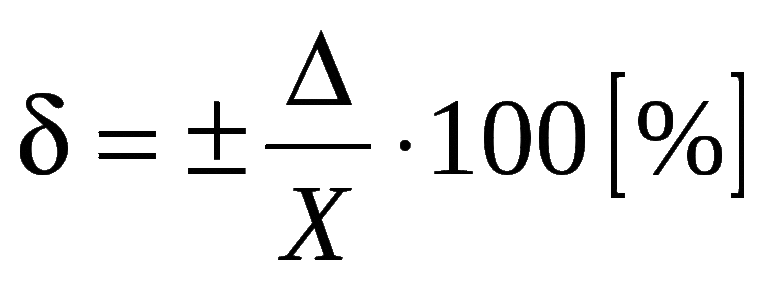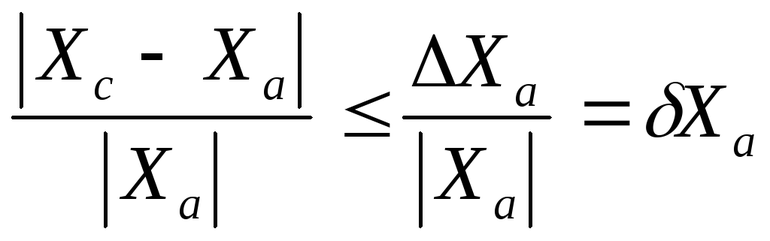Что называют относительной погрешностью приближенного числа
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
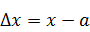
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
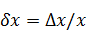
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

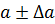
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 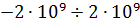
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
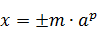
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 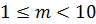
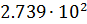
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 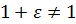
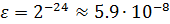
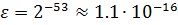
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
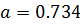
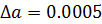
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
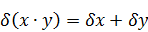
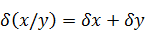
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
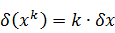
При сложении или вычитании чисел их абсолютные погрешности складываются:
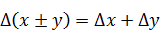
Относительная погрешность суммы положительных слагаемых вычисляется как:
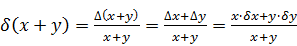
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
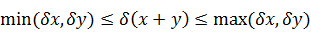
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 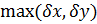
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 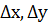
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.
В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.
Показатель бывает нескольких видов. Для его определения применяют разные методы.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:
Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г
Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Методики расчета
Существует несколько методов определения отклонения. Наиболее простой и доступный способ:
Для определения предельного отклонения выбирают наибольшее значение из всех полученных.
Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:
Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.
Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.
При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.
Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.
Методы Корнфельда и Стьюдента
Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.
Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:
Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.
Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.
Приближенное значение величины. Абсолютная и относительная погрешности
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
БИК Курс лекций по дисциплине «Численные методы»
Приближенные числа и действия над ними
1.1. Приближенное значение величины. Абсолютная и относительная погрешности
Приближенное значение величины. Погрешность
Абсолютная и относительная погрешности
1. Приближенное значение величины. Погрешность
В процессе решения задачи вычислитель сталкивается с различными числами, которые могут быть точными или приближенными. Точные числа дают истинное значение величины числа, приближенные – близкое к истинному, причем степень близости определяется погрешностью вычисления.
Например, в утверждениях: «куб имеет 6 граней»; «на руке 5 пальцев»; «в классе 32 ученика»; «в книге 582 страницы» числа 6, 5, 32, 582 – точные. В утверждениях: «ширина дома 14,25 м»; «вес коробки 50 г»; «в лесу около 5000 деревьев» числа 14,25; 50; 5000 – приближенные. Измерение ширины дома производится измерительными средствами, которые сами могут быть неточными; кроме того, измеритель при измерении допускает ошибку (погрешность). При взвешивании коробки также допускается ошибка, так как автоматические весы не чувствительны к увеличению или уменьшению веса на 0,5 г. Произвести точно подсчет количества деревьев в лесу невозможно, так как некоторые деревья могут быть подсчитаны дважды; другие совсем не включались в счет; некоторые деревья были отнесены к кустарникам и исключены из счета, и, наоборот, кустарники включены в счет количества деревьев.
Во многих случаях жизни невозможно найти точное значение величины числа и вычислителю приходится довольствоваться его приближенным значением. Кроме того, очень часто вычислитель сознательно заменяет точное значение приближенным в целях упрощения вычислений.
Таким образом, приближенным числом а называется число, незначительно отличающееся от точного числа А и заменяющее последнее в вычислениях.
При решении той или иной задачи вручную или на вычислительной машине мы получаем числовой результат, который, как правило, не является точным, так как при постановке задачи и в ходе вычислений возникают погрешности. Поэтому любая задача, связанная с массовыми действиями над числами, может быть решена с той или иной степенью точности. В связи с этим при постановке задачи должна быть указана точность ее решения, т. е. задана погрешность, максимально допустимая в процессе всех вычислений.
Источниками погрешностей (ошибок) могут быть:
1) неточное отображение реальных процессов с помощью математики, в связи с чем рассматривается не сам процесс, а его идеализированная математическая модель. Не всегда реальные явления природы можно точно отобразить математически. Поэтому принимаются условия, упрощающие решение задачи, что вызывает появление погрешностей. Некоторые задачи невозможно решить в точной постановке и они могут заменяться другими задачами, близкими по результатам первым. При этом также возникают погрешности;
2) приближенное выражение величин, входящих в условие задачи, вследствие их неточного измерения. Это погрешности исходных данных, физических констант, чисел π, е и др.;
3) замена бесконечных процессов, пределами которых являются искомые величины, конечной последовательностью действий. Сюда относятся погрешности, образующиеся в результате обрыва какого-то бесконечного процесса на некотором этапе. Например, если в ряде
взять определенное количество членов и принять их сумму за sin х, то мы, естественно, допускаем погрешность;
4) округление исходных данных, промежуточных или окончательных результатов, когда при вычислениях используется лишь конечное число цифр числа.
При отбрасывании младших разрядов числа имеет место погрешность. Пусть, например, число 0,7835478931 требуется записать в ячейку электронной цифровой вычислительной машины с разрядной сеткой, допускающей запись семизначного десятичного числа. Поэтому данное число нужно округлить так, чтобы в нем осталось не более семи знаков после запятой. Тогда округленное число примет следующий вид: 0,7835479;
5) кроме указанных выше случаев, погрешности могут появляться в результате действий над приближенными числами. В этом случае погрешности исходных данных в какой-то мере переносятся на результат вычислений.
Полная погрешность является результатом сложного взаимодействия всех видов погрешностей. При решении конкретных задач те или иные погрешности могут отсутствовать или мало влиять на образование полной погрешности. Однако для полного анализа погрешностей необходимо учитывать все их виды.
Во всех случаях полная погрешность не может превышать по своей абсолютной величине суммы абсолютных величин всех видов погрешностей, но обычно она редко достигает такой максимальной величины.
Таким образом, погрешности можно подразделить на три большие группы:
1) исходные, или неустранимые, к которым относятся погрешности, возникающие в результате приближенного описания реальных процессов и неточного задания исходных данных, а также погрешности, связанные с действиями над приближенными числами. Эти погрешности проходят через все вычисления и, являются неустранимыми;
2) погрешности округления (зарождающиеся), которые появляются в результате округления исходных данных, промежуточных и окончательных результатов;
3) остаточные, возникающие в результате замены бесконечных процессов конечной последовательностью действий;
2. Численные методы
На практике в большинстве случаев найти точное решение математических задач не удается. Это происходит главным образом не потому, что мы не умеем это сделать, а поскольку искомое решение обычно не выражается в привычным для нас элементарных или других известных функциях. Поэтому важное значение приобрели методы, особенно в связи с возрастанием роли математических методов в различных областях науки и техники и с появлением высокопроизводительных ЭВМ.
Под численными методами подразумевается методы решения задач, сводящиеся к арифметическим и некоторых логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ.
В зависимости от сложности задачи, заданной точности, применяемого метода и т.д. может потребоваться выполнить от нескольких десятков многих миллиардов действий. Если число действий не превышают тысячи, то с такой задачей обычно может справиться человек, имя в распоряжении калькулятор и набор таблиц элементарных функций. Однако без ЭВМ явно не обойтись, если для решения задач нужно выполнить, скажем, порядка миллиона действий и тем более, когда решение должно быть найдено в жатые сроки.
Решение, полученное численным методом, обычно является приближенным, т.е. содержит некоторую погрешность.
Оценка погрешности может быть произведена: с помощью абсолютной погрешности; с помощью относительной погрешности; с помощью остаточного члена; с помощью статистических оценок.
При работе с приближенными величинами вычислитель должен уметь:
а) давать математические характеристики точности приближенных величин;
б) зная степень точности исходных данных, оценить степень точности результатов;
в) брать исходные данные с такой степенью точности, чтобы обеспечить заданную точность результата. В этом случае не следует слишком завышать точность исходных данных, чтобы избавить вычислителя от бесполезных расчетов;
г) уметь правильно построить вычислительный процесс, чтобы избавить его от тех выкладок, которые не окажут влияния на точные цифры результата.
3. Абсолютная и относительная погрешности
Пусть a – точное, вообще говоря, неизвестное числовое значение некоторой величины.
a* – известное приближенное числовое значение этой величины (приближенное число).
Абсолютная величина разности между точным числом и его приближенным значением называется абсолютной погрешностью приближенного числа:

Здесь возможны два случая.
1. Точное чиcло а нам известно. Тогда абсолютная; погрешность приближенного числа легко находится по формуле (1).
Пример 1. Пусть a = 784,2737, a * = 784,274; тогда; абсолютная погрешность Δ а = | а- a * | = |784,2737—784,274| = 0,0003.
2. Точное число a нам неизвестно, тогда вычислить абсолютную погрешность по формуле (1) нельзя. Поэтому пользуются понятием границы абсолютной погрешности, удовлетворяющей неравенству
Граница абсолютной погрешности, т. е. число, заведомо превышающее абсолютную погрешность (или в крайнем случае равное ей), называется предельной абсолютной погрешностью.
Следовательно, если Δа* – предельная абсолютная погрешность, то
Δ(а*) = |а- a*| 
Значение точного числа А всегда заключено в следующих границах:
a* — Δа* 

Пример 2. Число 45,3 получено округлением. Точное значение числа неизвестно, однако, пользуясь правилами округления чисел, можно сказать, что абсолютная погрешность не превышает (меньше или равна) 0,05.
Следовательно, границей абсолютной погрешности (предельной абсолютной погрешностью) можно считать 0,05. Записывают это так: 45,3 ( ± 0,05). Скобки часто опускают, так что запись 45,3 ± 0,05 означает то же самое. Двойной знак ± означает, что отклонение приближенного значения числа от точного возможно в обе стороны. В качестве границы абсолютной погрешности берут по возможности наименьшее число.
Пример 3. При измерении длины отрезка оказалось, что ошибка, допущенная нами, не превышает 0,5 см; тем более она не превышает 1, 2 или 3 см. Каждое из этих чисел можно считать границей абсолютной погрешности. Однако нужно указать наименьшую из них, так как чем меньше граница абсолютной погрешности, тем точнее выражается приближенное значение числа. В записи приближенного числа, полученного в результате измерения, обычно отмечают его предельную абсолютную погрешность.
На практике часто применяют выражения типа: «с точностью до 0,01»; «с точностью до 1 см и т. д. Это означает, что предельная абсолютная погрешность соответственно равна 0,01; 1 см и т. д.
Пример 4. Если длина отрезка l = 184 см измерена с точностью до 0,05 см, то пишут l = 184 см ±0,05 см. Здесь предельная абсолютная погрешность Δ l *= 0,05 см, а точная величина длины l отрезка заключена в следующих границах: 183,95 см 

По абсолютной и предельной абсолютной погрешностям нельзя судить о том, хорошо или плохо произведено измерение.
Пример 5. Пусть при измерении книги и длины стола были получены результаты: l 1 = 28,4 ±0,1 (см) и l 2 = 110,3 ±0,1 (см). И в первом, и во втором случае предельная абсолютная погрешность составляет 0,1 см. Однако второе измерение было произведено более точно, чем первое.
Для того чтобы определить качество произведенных измерений, необходимо определить, какую долю составляет абсолютная или предельная абсолютная погрешность от измеряемой величины, В связи с этим вводится понятие относительной погрешности.
Относительной погрешностью 



Δ а = | A | 
Из соотношений (4) и (5) вытекает, что




Из определения предельной абсолютной погрешности следует, что Δ а 
Δ а * =| A | 
и за предельную относительную погрешность приближенного числа а можно принять


Учитывая, что А, как правило, неизвестно и что А 


Возвращаясь к примеру 5, найдем предельные относительные погрешности измерения книги и стола:




Таким образом, измерение стола было произведено намного точнее.
Очевидно, что как относительная погрешность, так и предельная относительная погрешность представляют собой отвлеченные числа, не зависящие от единиц, в которых выражаются результаты измерений.
Пример 6. Определить (в процентах) предельную относительную погрешность приближенного числа а = 35,148 ±0,00074.
Решение. Воспользуемся формулой (7). Тогда



Пример 7. Определить предельную абсолютную погрешность приближенного числа а = 4,123, если 
Решение. Запишем проценты в виде десятичной дроби и для определения предельной абсолютной погрешности и воспользуемся формулой (6′); тогда
Δ а * = | а | 
Пример 8. Определить относительные погрешности чисел х и у, полученных при измерении углов. Какой из результатов более точный?
Решение. Переведем заданные значения x и у в секунды и определим относительные погрешности измерений. Более точным измерением будет то, где относительная погрешность меньше. Имеем:
x = 181810″ ±3″, 

у = 162936″±2″, 

Измерение y произведено более точно.
Пример 9. Определить, какое равенство точнее: a 1 = 13/19 


Решение. Для нахождения предельных абсолютных погрешностей берем числа a 1 и a 2 с большим числом десятичных знаков: 13/19 

Δ * а 2 = | 7,2111-7,21 | 
Находим предельные относительные погрешности: