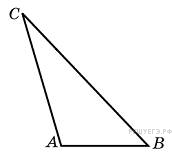
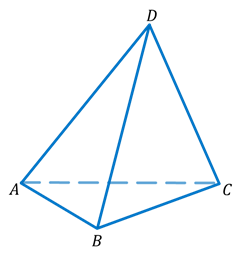
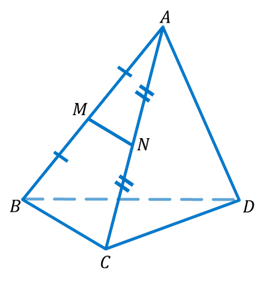
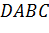Что называют основанием и боковыми гранями тетраэдра подпишите их на чертеже

Тетраэдр.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Основные формулы для правильного тетраэдра:

Источник

Лекция по математике на тему «Тетраэдр»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Лекция по теме «Тетраэдр»

Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».

Кристаллическая решетка метана

Тетрапакет для молока

Любимая игрушка моего детства Кубик Рубика

Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.

Многоугольник- часть плоскости, ограниченная замкнутой линией без самопересечений, включая ее саму.

А именно о тетраэдре.

Нужна анимационная картинка тетраэдра, которая вращается, грани раскрашены в разные оттенки зеленого цвета.

ТЕТРА́ЭДР [фр. tétraèdre геом. Четырехгранник, треугольная пирамида.

Проводить изучение многогранников будем по плану:

изображение на плоскости

План изучения многогранников:

изображение на плоскости

построим треугольник А BC

Пошагово появляется чертеж

Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.

Сколько граней, ребер и вершин имеет тетраэдр?

Желательно чтобы появился предыдущий рисунок и элементы подписывались на чертеже и указывались стрелочками по мере их прочтения.

Тетраэдр имеет четыре грани, шесть ребер и четыре вершины

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.

Появляется предыдущий рисунок, по мере чтения текста цветом на рисунке выделяются противоположные вершины

Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.

Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,

ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.

На экране появляется развертка тетраэдра.

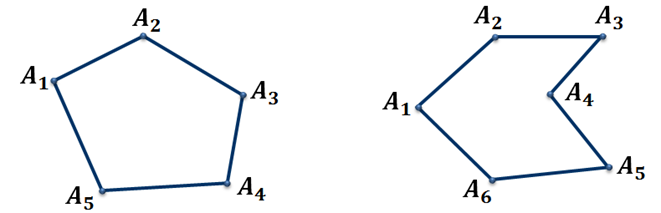
На плоскости тетраэдр изображается

В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.

Изображение тетраэдра на плоскости:

Решим несколько типовых задач на тетраэдр:

Найти площадь развертки правильного тетраэдра с ребром 5 см.

Решение. Начертим развертку тетраэдра

(на экране появляется развертка тетраэдра )

Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.

Площадь правильного треугольника ищем по формуле:

Задача 1. Найти площадь развертки правильного тетраэдра с ребром 5 см.

Площадь правильного треугольника:

Тогда получаем площадь тетраэдра равна:

Подставим в формулу длину ребра а=5 см,

Ответ: Площадь развертки правильного тетраэдра

Площадь полной поверхности правильного тетраэдра

б) ( Построение желательно делать поэтапно со словами диктора )

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-025600

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Апробацию новых учебников по ОБЖ завершат к середине 2022 года

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве

Время чтения: 1 минута

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Открытый урок по теме «Тетраэдр»

Содержимое разработки

Урок по теме «Тетраэдр».

Тип урока: введение нового материала

Основная дидактическая цель – сформировать представление о геометрическом теле– тетраэдре; познакомить учащихся с основными элементами и способами заданий тетраэдра, а также его использование при решении задач.

ввести понятие тетраэдра;

проиллюстрировать изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере тетраэдра;

рассмотреть задачи связанные с тетраэдром;

умением владеть символическим языком.

развить самостоятельную познаваемость, творческую активность;

логическое, пространственное, визуальное т.п. мышление;

геометрическую интуицию на образы, свойства, методы построения.

воспитывать интерес к математике,

уважение друг к другу при работе в группе.

1.Организационный момент, цель урока.

2. Актуализация знаний учащихся

3. Изучение нового материала. (Работа в группах)

4. Исследовательская деятельность уч-ся( доклад по теме урока).

5. Физминутка. (Гимнастика для глаз)

6. Закрепление нового материала( решение задач).

8.Подведение итога урока, оценивание уч-ся.

I. Организационный момент

Среди занимательных задач есть такая: Из 6 спичек сложите 4 треугольника так, чтобы каждая сторона была одна спичка. У вас на столах лежат 6 спичек. Попробуйте и вы решить эту задачу. (Работа в парах)

С этой фигурой мы уже встречались на уроках геометрии. Как называется фигура?

Значит тема урока Тетраэдр.

Ребята, какие новые понятия и элементы вы бы хотели бы узнать об этой фигуре?

— Почему он называется тетраэдром?

— Какие элементы мы будем в нем изучать?

-Какую роль он играет в математике? И т.д.

Ребята, вы сами сейчас поставили цель нашего сегодняшнего урока: Дать понятие тетраэдра, элементов тетраэдра, значимость этой фигуры в геометрии.

Глядя на нашу фигуру, давайте мы с вами вместе постараемся выяснить из чего он состоит.

II. Устная работа (Актуализация знаний).

Мы решим несколько несложных задач, предлагаемых учащимся при сдаче выпускного экзамена в форме ЕГЭ,

Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.

Сумма двух углов треугольника и внешнего угла к третьему равна 40°. Найдите этот третий угол. Ответ дайте в градусах.

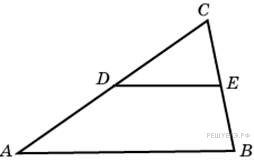
Площадь треугольника ABC равна 4. DE— средняя линия. Найдите площадь треугольника CDE.

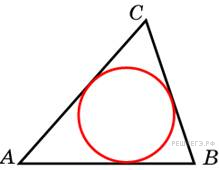
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.

III. Изучение нового материала.

Изучая фигуры в пространстве необходимо составить план изучения этой фигуры. На доске прикреплены этапы изучения темы. (Определение, свойства, элементы, обозначения, чертеж) Слова заданы без определенного порядка. Необходимо составить план. Как вы думаете каков он может быть?

Используя план, составленный вами, начнем изучение нового понятия.

На столах у учащихся листы с таблицей

Инструкция к работе:

I. Составить истинные высказывания:

Грани тетраэдра – это…

Вершины тетраэдра – это…

Противоположные ребра тетраэдра – это…

Основание тетраэдра, боковые ребра тетраэдра…

II. Изображение тетраэдра (различные способы)

III. Обозначение тетраэдра (два примера)

Отчет о работе групп

Первая группа – определение тетраэдра.

Вторая группа – элементы тетраэдра

Третья группа – Изображение тетраэдра

Четвертая группа – Обозначение (в сопровождении с изображением)

IV. Сообщение обучающегося

Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. Сообщение ученика «Тетраэдр в деятельности человека».

V. Гимнастика для глаз.

1) Изучение этого многогранника даст возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей в пространстве.

Решим следующие задачи устно

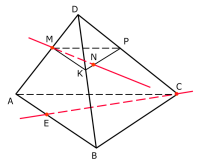
Задача 1: Ответьте на вопросы слайда:

Каково взаимное расположение прямой МN и плоскости АВС?

Каково взаимное расположение прямой МN и прямой ЕС?

Каково взаимное расположение прямой МN и прямой АF?

К доске ученик, остальные в тетрадях

VI. Тест (контроль первичных знаний)

А) 4 треугольников Б) 3 треугольников

В) 5 треугольников Г) 4 четырехугольников

2) Концы ребер многоугольника называют….

А) грани б) ребра в) вершины г) диагонали

3) В тетраэдре МРКС треугольник РКС является:

А) боковой гранью: Б) ребром; В) основанием; Г) вершиной.

4) Какого взаимное расположение прямой ЕС и плоскости (МКР)

А) пересекаются, Б) параллельны, В) прямая принадлежит плоскости, Г) скрещиваются

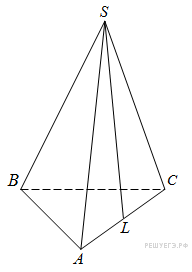
5) Решите задачу: Все ребра тетраэдра SABC равны, точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь всех боковых граней тетраэдра.

А) 90; Б) 36; В) 45; Г) 150.

1) В тетраэдре DABC противоположными являются ребра:

А) DB и ВС; Б) DА и ВС; В) АС и ВС; В) DС и ВD.

2) Гранями тетраэдра являются:

А) отрезки; Б) четырехугольники; В) треугольники; В) прямые

3) Сколько ребер у тетраэдра?

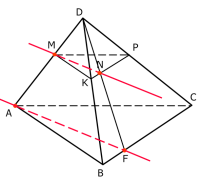
4) Каково взаимное расположение прямой AF и плоскости (МКР)

А) пересекаются, Б) параллельны, В) прямая принадлежит плоскости, Г) скрещиваются

Источник

Тетраэдр

Урок 12. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Тетраэдр»

В начале изучения курса «Стереометрии» мы говорили, что все геометрические тела делятся на тела вращения и многогранники. В процессе изучения геометрии в десятом классе, мы будем подробно рассматривать с вами свойства тех или иных фигур.

Сегодня мы познакомимся с такой фигурой как тетраэдр. Прежде чем приступить к изучению пространственной фигуры, давайте вернемся в планиметрию и вспомним такую фигуру как многоугольник.

Напомню, что многоугольником называется либо замкнутая линия без самопересечений либо часть плоскости, ограниченная этой линией, включая ее саму.

Для стереометрии нам естественно подходит второе определение. Это определение показывает, что каждый многоугольник представляет собой плоскую поверхность.

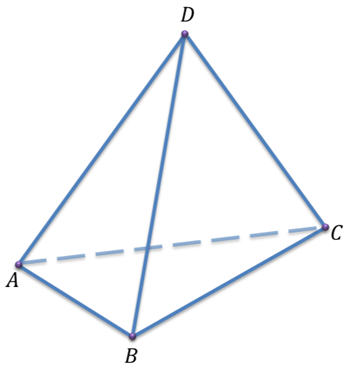
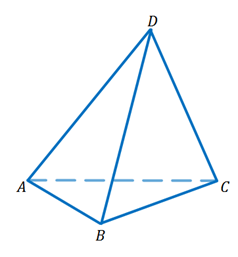
Напомним, что простейшим многоугольником является треугольник. Возьмем треугольник ABC и точку D, которая не лежит в плоскости треугольника ABC. Соединим точку D с каждой вершиной треугольника ABC. Таким образом, мы получим три новых треугольника DAB, DBC, DCA. Тогда фигуру, которая состоит из четырех треугольников ABC, DAB, DBC, DCA, называют тетраэдром и обозначают так: DABC.

Треугольники, из которых состоит тетраэдр, называются гранями, стороны этих треугольников называют ребрами, вершины этих треугольников называются вершинами тетраэдра.

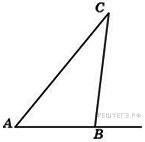
Нетрудно посчитать, что тетраэдр имеет четыре грани, 6 ребер и четыре вершины. Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Давайте запишем пары противоположных ребер тетраэдра, который изображен на рисунке.

Это будут ребра AD и BC, BDи AC, CD и AB. Иногда одну из граней тетраэдра называют основанием, а три другие – боковыми гранями.

Слово тетраэдр произошло от древнегреческих слов теторес – четыре и эдра – основание или грань.

Если все грани тетраэдра – равносторонние треугольники, то такой тетраэдр называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями.

Последователи Пифагорейской философской школы форму тетраэдра придавали стихии огня.

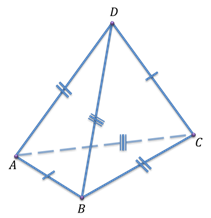
Тетраэдр, все грани которого равные между собой треугольники, называется равногранным тетраэдром.

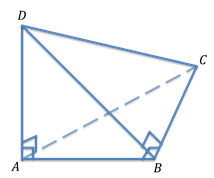
Если ребра тетраэдра, которые прилегают к одной вершине, перпендикулярны между собой, то такой тетраэдр называется прямоугольным.

Тетраэдры обычно изображаются в виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.

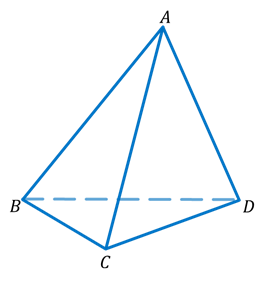
На этом рисунке невидимым является только ребро AC.

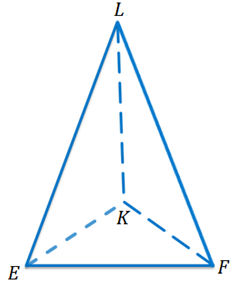
А на этом рисунке невидимыми являются ребра ЕК, KF, KL.

Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов.

Ярким примером тетраэдра является разработанное для Нового Орлеана «здание-город», которое возвышается на 360 метров, включает в себя 20000 квартир, суммарная жилая площадь которых 2040000 квадратных метров. Здание использует экологичное энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре помещаются коммерческие организации, три отеля, культурные объекты, школа, больницы и казино. И, учитывая место, под которое создавался проект, его немаловажная особенность — способность держаться на плаву.

Решим насколько задач.

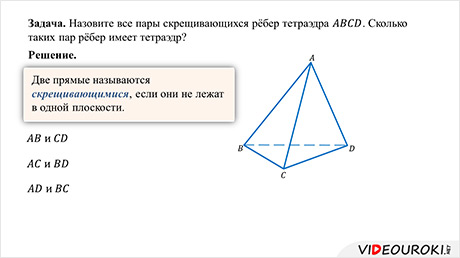
Задача. Назовите все пары скрещивающихся рёбер тетраэдра 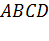. Сколько таких пар рёбер имеет тетраэдр?

Напомним, что две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Нетрудно увидеть, что скрещивающимися будут ребра AB и СD, АC и BD, АD и BC. То есть в тетраэдре есть три пары скрещивающихся ребер.

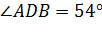
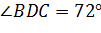
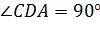
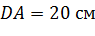
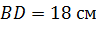
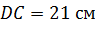
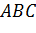
Задача. В тетраэдре , , , , , . Найти рёбра основания данного тетраэдра.

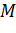
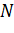
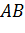
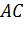
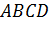
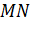
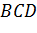
Задача. Пусть точки и – середины рёбер и тетраэдра . Доказать, что прямая параллельна плоскости .

Что и требовалось доказать.

Подведем итоги урока. Сегодня на уроке мы познакомились с пространственным многогранником – тетраэдром. Познакомились с элементами тетраэдра, решили несколько задач по данной теме.

Источник