Что называют объединением событий а и в
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет 
, потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом: 
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).
Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.
Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – 
. Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: 
.
Подборку задач на отработку темы смотрите здесь.
Что называют объединением событий а и в
тБУУНПФТЙН НОПЦЕУФЧП F УПВЩФЙК, ЛПФПТЩЕ НПЦОП ОБВМАДБФШ Ч ОЕЛПФПТПН УМХЮБКОПН ЬЛУРЕТЙНЕОФЕ. рХУФШ 
– ДПУФПЧЕТОПЕ УПВЩФЙЕ, Б 
– ОЕЧПЪНПЦОПЕ, ФБЛЦЕ РТЙОБДМЕЦБФ НОПЦЕУФЧХ F.
лБЦДПНХ УПВЩФЙА б РПУФБЧЙН Ч УППФЧЕФУФЧЙЕ РТПФЙЧПРПМПЦОПЕ (ДПРПМОЙФЕМШОПЕ) УПВЩФЙЕ, ПВПЪОБЮБЕНПЕ 
Й ПЪОБЮБАЭЕЕ, ЮФП УПВЩФЙЕ ТЕБМЙЪХЕФУС ФПЗДБ Й ФПМШЛП ФПЗДБ, ЛПЗДБ УПВЩФЙЕ б ОЕ ТЕБМЙЪХЕФУС. чЧЕДЕН ЛБЛ БЛУЙПНЩ УМЕДХАЭЙЕ УЧПКУФЧБ ЬФПК ПРЕТБГЙЙ:
; 
; 
.
рТЙНЕТБНЙ РТПФЙЧПРПМПЦОЩИ УПВЩФЙК НПЗХФ УМХЦЙФШ РПРБДБОЙЕ Й РТПНБИ РТЙ ЧЩУФТЕМЕ, ПФЛБЪ РТЙВПТБ Ч ДБООПН ЙОФЕТЧБМЕ ЧТЕНЕОЙ Й ЕЗП ЙУРТБЧОБС ТБВПФБ Ч ФПН ЦЕ ЙОФЕТЧБМЕ ЧТЕНЕОЙ.
дМС ЛБЦДПК РБТЩ УПВЩФЙК б Й ч ЧЧЕДЕН ПРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС.
уПВЩФЙЕ 
ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП ЙЪ ДЧХИ УПВЩФЙК б Й ч РТПЙУИПДЙФ РП ЛТБКОЕК НЕТЕ ПДОП, ОБЪЩЧБАФ ПВЯЕДЙОЕОЙЕН УПВЩФЙК б Й ч.
уПВЩФЙЕ 
(бч), ЪБЛМАЮБАЭЕЕУС Ч ФПН, ЮФП РТПЙУИПДСФ ПДОПЧТЕНЕООП ПВБ УПВЩФЙС б Й ч, ОБЪЩЧБАФ РЕТЕУЕЮЕОЙЕН УПВЩФЙК б Й ч.
пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС ЛПННХФБФЙЧОЩ Й БУУПГЙБФЙЧОЩ
; 
; 
; 
.
уМЕДХАЭЙЕ ЖПТНХМЩ ЧЧПДСФУС ЛБЛ БЛУЙПНЩ:
чЧЕДЕООЩЕ УППФОПЫЕОЙС РЕТЕОПУСФУС У ДЧХИ УПВЩФЙК ОБ РТПЙЪЧПМШОПЕ ЛПОЕЮОПЕ ОЕРХУФПЕ УЕНЕКУФЧП УПВЩФЙК 
.
пРЕТБГЙЙ ПВЯЕДЙОЕОЙС Й РЕТЕУЕЮЕОЙС, ОБЛПОЕГ, ДЙУФТЙВХФЙЧОЩ РП ПФОПЫЕОЙА ДТХЗ Л ДТХЗХ:
; 
.
уФТХЛФХТБ, ЛПФПТБС ПВТБЪХЕФУС ОБ НОПЦЕУФЧЕ УПВЩФЙК ЧЧЕДЕООЩНЙ ПРТЕДЕМЕОЙСНЙ Й БЛУЙПНБНЙ, ОБЪЩЧБЕФУС УФТХЛФХТПК ВХМЕЧПК БМЗЕВТЩ. тБУУНПФТЙН ЧУРПНПЗБФЕМШОЩЕ РПОСФЙС, ПРТЕДЕМСЕНЩЕ ОБ ВХМЕЧПК БМЗЕВТЕ УПВЩФЙК.
дЧБ УПВЩФЙС б Й ч, ДМС ЛПФПТЩИ 
ОБЪЩЧБАФУС ОЕРЕТЕУЕЛБАЭЙНЙУС (ЧЪБЙНОП ЙУЛМАЮБАЭЙНЙ). пВЯЕДЙОЕОЙЕ ФБЛЙИ УПВЩФЙК ОБЪЩЧБАФ УХННПК Й ПВПЪОБЮБАФ б + ч ЧНЕУФП 
.
тБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ б – ч, УПУФПСЭЙЕ Ч ФПН, ЮФП РТПЙЪПКДЕФ УПВЩФЙЕ б Й ОЕ РТПЙЪПКДЕФ УПВЩФЙЕ ч. пЮЕЧЙДОП, ЮФП 
.
уЙННЕФТЙЮЕУЛПК ТБЪОПУФША ДЧХИ УПВЩФЙК б Й ч ОБЪЩЧБАФ УПВЩФЙЕ 
, ПЪОБЮБАЭЕЕ, ЮФП РТПЙУИПДЙФ МЙЫШ ПДОП ЙЪ б, ч.
уПВЩФЙС 
ПВТБЪХАФ РПМОХА ЗТХРРХ УПВЩФЙК, ЕУМЙ ПОЙ РПРБТОП ОЕ РЕТЕУЕЛБАФУС (ОЕУПЧНЕУФОЩ) Й 
, ФП ЕУФШ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ РТПЙУИПДЙФ ПДОП Й ФПМШЛП ПДОП ЙЪ ОЙИ.
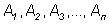
зПЧПТСФ, ЮФП УПВЩФЙЕ б ЧМЕЮЕФ УПВЩФЙЕ ч (ПВПЪОБЮБАФ 
), ЕУМЙ УПВЩФЙЕ ч ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ УПВЩФЙС б. еУМЙ УПВЩФЙС б Й ч НПЗХФ РПСЧЙФШУС ЙМЙ ОЕ РПСЧЙФШУС ФПМШЛП ЧНЕУФЕ, ФП ЕУФШ Й 
, ФП ПОЙ ОБЪЩЧБАФУС ЬЛЧЙЧБМЕОФОЩНЙ (б = ч). ьЛЧЙЧБМЕОФОЩЕ УПВЩФЙС ТБЪМЙЮБФШ ОЕ ВХДЕН. пФОПЫЕОЙЕ «ЧМЕЮЕФ» СЧМСЕФУС ПФОПЫЕОЙЕН РПТСДЛБ Ч НОПЦЕУФЧЕ УПВЩФЙК.
вТПУБАЭБСУС Ч ЗМБЪБ БОБМПЗЙС НЕЦДХ УПВЩФЙСНЙ Й НОПЦЕУФЧБНЙ ПВЯСУОСЕФУС ФЕН, ЮФП ЛБЦДПЕ УПВЩФЙЕ УЧСЪБОП У ПРТЕДЕМЕООЩН НОПЦЕУФЧПН ЙУИПДПЧ ЬЛУРЕТЙНЕОФБ ФБЛ, ЮФП ПОП ПВСЪБФЕМШОП РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ, Й ОЕ РТПЙУИПДЙФ РТЙ РПСЧМЕОЙЙ ПДОПЗП ЙЪ ЙУИПДПЧ, ОЕ РТЙОБДМЕЦБЭЙИ ЬФПНХ НОПЦЕУФЧХ. оБРТЙНЕТ, УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ, ЕУФШ УХННБ ДЧХИ ОЕРЕТЕУЕЛБАЭЙИУС УПВЩФЙК: РПРБДБОЙЕ 
РТЙ РЕТЧПН Й РТПНБИ 
РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН 
Й РПРБДБОЙЕ 
РТЙ ЧФПТПН ЧЩУФТЕМЕ
.
дМС УФТПЗПЗП НБФЕНБФЙЮЕУЛПЗП ПВПУОПЧБОЙС, ЧЧПДСФ РПОСФЙЕ ЬМЕНЕОФБТОПЗП УПВЩФЙС.
ьМЕНЕОФБТОЩН УПВЩФЙЕН ОБЪЩЧБЕФУС УПВЩФЙЕ, ОЕ УПДЕТЦБЭЕЕ ОЙЛБЛЙИ РПДУПВЩФЙК, ЛТПНЕ ОЕЧПЪНПЦОПЗП УПВЩФЙС Й УБНПЗП УЕВС
ч ТБНЛБИ ЬЛУРЕТЙНЕОФБ, ЬМЕНЕОФБТОПЕ УПВЩФЙЕ ЬФП ТЕЪХМШФБФ ЬЛУРЕТЙНЕОФБ. лБЦДПЕ, ПФОПУСЭЕЕУС Л ТБУУНБФТЙЧБЕНПК НПДЕМЙ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ, ЧМЕЮЕФ МЙВП ОБУФХРМЕОЙЕ, МЙВП ОЕ ОБУФХРМЕОЙЕ ЛБЦДПЗП ДБООПЗП УПВЩФЙС, УЧСЪБООПЗП У ТБУУНБФТЙЧБЕНПК НПДЕМША. оБРТЙНЕТ, РТЙ ПДОПН ЧЩУФТЕМЕ РП НЙЫЕОЙ ЬМЕНЕОФБТОЩН УПВЩФЙЕН ВХДХФ РТПНБИ Й РПРБДБОЙЕ. ч ЬЛУРЕТЙНЕОФЕ – РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ ВХДЕФ ПДОП РПРБДБОЙЕ – ЬМЕНЕОФБТОЩНЙ УПВЩФЙСНЙ ВХДХФ: РПРБДБОЙЕ РТЙ РЕТЧПН Й РТПНБИ РТЙ ЧФПТПН ЧЩУФТЕМЕ Й РТПНБИ РТЙ РЕТЧПН Й РПРБДБОЙЕ РТЙ ЧФПТПН ЧЩУФТЕМЕ.
уМХЮБКОЩК ЬЛУРЕТЙНЕОФ ОБЪЩЧБЕФУС ЛПОЕЮОЩН, ЕУМЙ ЙНЕЕФУС РПМОБС ЗТХРРБ ЬМЕНЕОФБТОЩИ УПВЩФЙК.
ч ФЕПТЙЙ ЧЕТПСФОПУФЕК ТБУУНБФТЙЧБАФУС МЙЫШ ФБЛЙЕ УМХЮБКОЩЕ ЬЛУРЕТЙНЕОФЩ, Ч ЛПФПТЩИ ЛБЦДПЕ УПВЩФЙЕ СЧМСЕФУС УХННПК ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК, ЧМЕЛХЭЙИ ЬФП УПВЩФЙЕ. фБЛПК УМХЮБКОЩК ЬЛУРЕТЙНЕОФ ПРЙУЩЧБЕФУС НОПЦЕУФЧПН ЬМЕНЕОФБТОЩН УПВЩФЙК, УЧСЪБООЩИ У ОЙН Й ОЕЛПФПТЩН ЛМБУУПН ЕЗП РПДНОПЦЕУФЧ, ОБЪЩЧБЕНЩИ УПВЩФЙСНЙ Й ОБЪЩЧБЕФУС РТПУФТБОУФЧПН ЬМЕНЕОФБТОЩИ УПВЩФЙК. пВПЪОБЮБЕФУС ПВЩЮОП 
. рТЙ ЬФПН МАВПЕ ЬМЕНЕОФБТОПЕ УПВЩФЙЕ – ФПЮЛБ РТПУФТБОУФЧБ ПВПЪОБЮБЕФУС ВХЛЧПК 
.
дПУФПЧЕТОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК НОПЦЕУФЧП ЧУЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК . оЕЧПЪНПЦОПЕ УПВЩФЙЕ РТЕДУФБЧМСЕФ УПВПК РХУФПЕ НОПЦЕУФЧП 
.
оБРТЙНЕТ, РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК Ч ЬЛУРЕТЙНЕОФЕ, ЪБЛМАЮБАЭЕНУС Ч ФПН, ЮФП ОБВМАДБЕФУС РПРБДБОЙЕ ЙМЙ РТПНБИ РТЙ ДЧХИ ЧЩУФТЕМБИ РП НЙЫЕОЙ УПУФПЙФ ЙЪ ЮЕФЩТЕИ ЬМЕНЕОФБТОЩИ УПВЩФЙК: ДЧБ РПРБДБОЙС, РПРБДБОЙЕ – РТПНБИ, РТПНБИ – РПРБДБОЙЕ, ДЧБ РТПНБИБ.
дМС ОБЗМСДОПУФЙ РПУФТПЕООПК НБФЕНБФЙЮЕУЛПК НПДЕМЙ УМХЮБКОЩИ СЧМЕОЙК ХДПВОП ХУМПЧОП УЮЙФБФШ РТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ОЕЛПФПТПК ПВМБУФША РМПУЛПУФЙ (ЛЧБДТБФПН), ЬМЕНЕОФБТОПЕ УПВЩФЙЕ — ФПЮЛБНЙ ЬФПК ПВМБУФЙ; РТЙ ЬФПН УПВЩФЙС ХДПВОП ЙЪПВТБЦБФШ Ч ЧЙДЕ ОЕЛПФПТЩИ ЖЙЗХТ (ЛТХЗПЧ).
оБ ТЙУХОЛБИ РТЕДУФБЧМЕОЩ ЙЪПВТБЦЕОЙС УМЕДХАЭЙИ ПРЕТБГЙК:
Б). б Й ч – ОЕУПЧНЕУФОЩЕ УПВЩФЙС;
В).— ПВЯЕДЙОЕОЙЕ УПВЩФЙК б Й ч;
Ч). бч – РЕТЕУЕЮЕОЙЕ УПВЩФЙК б Й ч;
З). б – ч – ТБЪОПУФШ УПВЩФЙК б Й ч;
Д). — РТПФЙЧПРПМПЦОПЕ Л б УПВЩФЙЕ;
Е). — УПВЩФЙЕ ч ЧМЕЮЕФ УПВЩФЙЕ б.
чБЦОЩН РТЙНЕТПН УМХЮБКОПЗП ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ЬЛУРЕТЙНЕОФ, Ч ЛПФПТПН ЙЪНЕТСЕФУС ОЕЛПФПТБС ЧЕМЙЮЙОБ и. ч ЛБЮЕУФЧЕ ЬМЕНЕОФБТОЩИ УПВЩФЙК ЪДЕУШ НПЦОП ЧЪСФШ УПВЩФЙС ЧЙДБ (и = И), ЗДЕ И – ОЕЛПФПТПЕ ЖЙЛУЙТПЧБООПЕ ЪОБЮЕОЙЕ. нОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК ЕУФЕУФЧЕООП ПФПЦДЕУФЧЙФШ У НОПЦЕУФЧПН ФПЮЕЛ ОБ РТСНПК. еУМЙ БРТЙПТЙ ЙЪЧЕУФОП, ЮФП и НПЦЕФ РТЙОЙНБФШ МЙЫШ ЪОБЮЕОЙС ЙЪ ОЕЛПФПТПЗП НОПЦЕУФЧБ н, ФП ЬФП НОПЦЕУФЧП Й УМЕДХЕФ ТБУУНБФТЙЧБФШ ЛБЛ НОПЦЕУФЧП ЬМЕНЕОФБТОЩИ УПВЩФЙК. ч РТПГЕУУЕ ЙЪНЕТЕОЙС ЕУФЕУФЧЕООП РТЕДРПМБЗБФШ ЧПЪНПЦОПУФШ ОБВМАДЕОЙС УПВЩФЙС 
, ЗДЕ Б Й b – РТПЙЪЧПМШОЩЕ ЮЙУМБ. чУЕЧПЪНПЦОЩЕ ЛПОЕЮОЩЕ УХННЩ ФБЛЙИ РПМХЙОФЕТЧБМПЧ НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ БМЗЕВТХ УПВЩФЙК, УЧСЪБООЩИ У ЬЛУРЕТЙНЕОФПН.
Артём Санников
Языки программирования
Базы данных
Программное обеспечение
Операционные системы
Мобильная разработка
Менеджеры пакетов
Сетевые технологии
CMS системы
Математика
SEO продвижение
Социальные сети
Психология
Хостинг провайдер
Смартфоны
Операции над событиями. Теория вероятностей
Пересечение событий
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
События не пересекаются
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода
Анализ события B: этому событию соответствует три элементарных исхода
После анализа событий приступаем к пошаговому решению.
Отсюда мы можем посчитать вероятность этого события:
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
Другие статьи из категории «Теория вероятностей»
Что называют объединением событий а и в
Аксиомы сложения и умножения вероятностей
Событие, состоящее в ненаступлении случайного события А, называется событием, противоположным событию А, и обозначается через 
. Объединение событий А и дает событие достоверное, а так как события А и несовместны, то
Пересечением (или совмещением, произведением ) двух случайных событий А1 и А2 называется сложное событие, заключающееся в одновременном или последовательном осуществлении обоих событий. Совмещение событий А1 и А2 обозначается через А1∩А2 или А1А2.
Под условной вероятностью события А2 по отношению к событию А1 [обозначается Р(А2/А1)] понимается вероятность осуществления события А2, определенная в предположении, что событие А1 имело место.
Вероятность совмещения двух событий А1 и А1 равна произведению вероятности одного из них на условную вероятность второго по отношению к первому ( аксиома умножения вероятностей ):
Для независимых событий вероятность их совмещения равна произведению их вероятностей:
Рейтинг: 2.6/5 (Всего оценок: 18)
Суммой, или объединением, двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма двух событий
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Модуль: Действия над событиями.
Действия над событиями.
Произведением или пересечением, двух событий называется событие, состоящее в одновременном их появлении. Произведение двух событий A и В обозначается через АВ или 
. Аналогично определяется и обозначается произведение в случае большего числа событий.
Сложение и умножение вероятностей
Теорема сложения вероятностей двух событий
Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Теорема сложения вероятностей двух несовместных событий
Вероятность суммы двух несовместных событий равна сумме веро ятностей этих событий:
Теорема сложения вероятностей n несовместных событий
Сумма вероятностей событий 
образующих полную группу, равна единице: 
Сумма вероятностей противоположных событий равна единице:
Вероятность события В при условии, что произошло событие А, называется условной вероятностью события В и обозначается так: Р(В/А),или Р А (В).
Теорема умножения вероятностей
Вероятность произведения двух событий равна произведению веро ятности одного из них на условную вероятность другого при условии, что первое событие произошло:
Р(АВ) = Р(А)Р(В/А), Р(АВ) = Р(В)Р(А/В).
Событие В не зависит от события А, если Р(В/А) = Р(В),
т.е. вероятность события В не зависит от того, произошло ли событие А.
Теорема умножения вероятностей двух независимых событий
Вероятность произведения двух независимых событий равна произ ведению их вероятностей:
Теорема умножения вероятностей n событий
Вероятность произведения п событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в пред положении, что все предыдущие события наступили:
В частности, для трех событий А, В, С формула принимает вид
Теорема умножения вероятностей n независимых событий
Если события независимы, то вероятность их произведения равна произведению вероятностей этих событий:
Если независимые события имеют одинаковую вероятность, равную р, то вероятность появление хотя бы одного из этих событий выражается формулой
Подбрасывается игральный кубик. Чему равна вероятность того, что выпадет четное число очков?
В урне находится 8 красных и 6 голубых шаров. Из урны последовательно без возвращения извлекается 3 шара. Найти вероятность того, что все 3 шара голубые.
Используя теоремы умножения и суммы решить данные задания
В урне 40 шариков: 15 голубых, 5 зеленых и 20 белых. Какова вероятность того, что из урны будет извлечен цветной шарик? (1/2)
Подбрасывается два игральных кубика. Найти вероятность события А-«сумма выпавших очков не превосходит четырех».(1/6)
Симметричная монета подброшена три раза. Какова вероятность того, что цифра выпадет ровно два раза? (3/8)
Три стрелка попадают в мишень соответственно с вероятностями 0,85, 0,8, 0,7. Найти вероятность того, что при одном выстреле хотя бы один из них попадет в мишень.(0,991)
Сколько раз нужно подбросить два игральных кубика, чтобы вероятность выпадения хотя бы один раз двух шестерок была бы больше 1/2? (25)
Вероятность того, что событие появится хотя бы один раз в трех независимых испытаниях, равна 0,973. Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же). (0.7)