Что называют множеством объектов
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
Выделяют три вида множеств:
пустые (обозначаются Ø) – не имеющие элементов.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
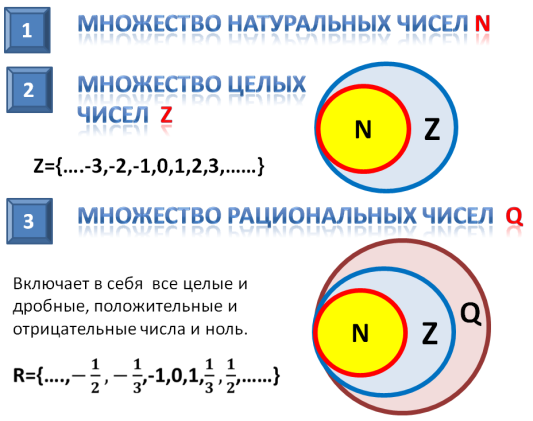
Множество натуральных чисел
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
Следовательно, N и Z являются подмножествами Q.
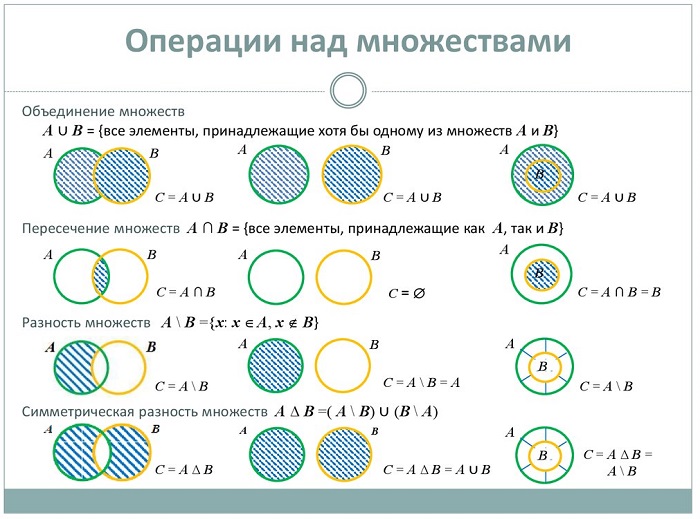
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
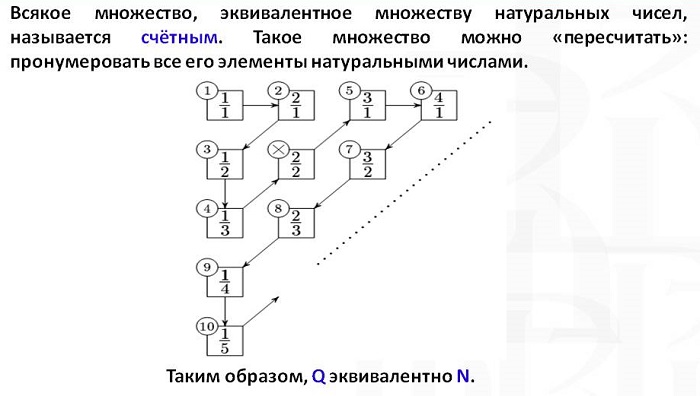
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
§1. Множества и операции над ними
Объяснение и обоснование
В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = <1; 2; 3>. Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например: множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.
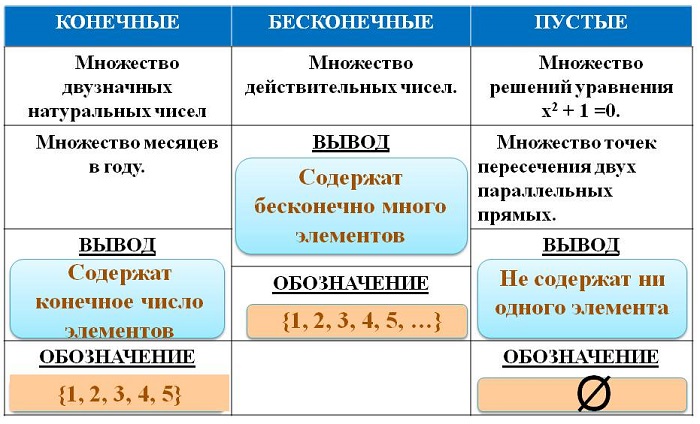
Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = <7>и M = <1; 2; 3>— конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = <–1; 0; 1>(множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B =
В общем виде запись множества с помощью характеристического свойства можно обозначить так: A =
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, <1; 2; 2>= <1; 2>, поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A ⊂ B.
Например, <1; 2>⊂ <0; 1; 2; 3>, N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).
Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.
Иногда вместо записи A ⊂ B используется также запись A ⊆ B.
Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,
два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.
Математическое множество
Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).
Содержание
Теории
Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.
«Наивная теория множеств»
Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам, возникающим из-за того, что интуитивное понятие «чётко определённый» на самом деле само не определено чётко. Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий, становится очевидной необходимость её строгой аксиоматизации.
Наивная теория множеств была создана Кантором в конце XIX века.
История определения
До XIX века считалось, что точного определения множества нет. Множеством считалось любое скопление предметов.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Аксиоматическая теория множеств
На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).
Некоторые виды множеств
Множество множеств Подмножество Надмножество
Операции над множествами
Литература
См. также
Полезное
Смотреть что такое «Математическое множество» в других словарях:
Множество Витали — Множество Витали первый пример множества вещественных чисел, не имеющего меры Лебега. Этот пример, ставший классическим, опубликовал в 1905 году итальянский математик Дж. Витали в своей статье «Sul problema della misura dei gruppi di punti… … Википедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
Математическое обеспечение АСУ — [MIS software ], то же, что программное обеспечение, ПО, комплекс математических программ и алгоритмов, одна из обеспечивающих подсистем. Обычно включает множество программ для решения на ЭВМ конкретных задач, объединяемых главной программой… … Экономико-математический словарь
математическое обеспечение АСУ — то же, что программное обеспечение, ПО, комплекс математических программ и алгоритмов, одна из обеспечивающих подсистем. Обычно включает множество программ для решения на ЭВМ конкретных задач, объединяемых главной программой диспетчером.… … Справочник технического переводчика
Множество — (математическое) см. Множеств теория … Большая советская энциклопедия
Математическое моделирование — Математическая модель это математическое представление реальности[1]. Математическое моделирование процесс построения и изучения математических моделей. Все естественные и общественные науки, использующие математический аппарат, по сути… … Википедия
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). М. п.… … Математическая энциклопедия
Математическое программирование — математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). М. п. раздел науки об… … Большая советская энциклопедия
Математическое доказательство — У этого термина существуют и другие значения, см. Доказательство. В математике доказательством называется цепочка логических умозаключений, показывающая, что при каком то наборе аксиом и правил вывода верно некоторое утверждение. В зависимости от … Википедия
Объекты и множества — что это?свойства и совокупность
Объекты и множества — что это? свойства и совокупность
Мир, который нас окружает, — это мир предметов, явлений и процессов. С самого рождения человек познаёт окружающий его мир. Растения и животные, горы и реки, материки и страны, планеты и звёзды, полёт птицы или строительство дома – всё это становится для нас объектами познания.
Объект – это любая часть окружающей действительности, которую человек воспринимает как единое целое. Другими словами, объект – это то, на что обращено наше внимание: предметы, процессы и явления
Например, компьютерный стол, учебник, окно, попугай – это объекты-предметы; гроза, дождь, град, лунное затмение – объекты-явления; отпуск, прослушивание музыкальной композиции, высаживание рассады – это объекты-процессы.
Задание. Назовите предметы, явления и процессы, с которыми имеет дело человек, когда:
Совокупность объектов, объединённых каким-либо общим признаком, называется множеством, а каждый из этих объектов – элементом множества.
Вопрос. Если врач – это множество, то каковы элементы этого множества?
Множество может быть конечным и бесконечным (множество страниц книги и множество действительных чисел), упорядоченным и неупорядоченным (то есть элементы которого выстроены по какому-либо порядку или выстроены беспорядочно), пустым и непустым.
Пустое множество – множество, не содержащее ни одного элемента: например, множество сиамских кошек, множество решений уравнения x 2 – 5x + 6 = 0. Говорят, что пустое множество является своим подмножеством, но не является своим элементом.
Задание.Распределите данные примеры множеств таким образом, чтобы в каждой группе множеств находилось по два примера.
| Конечное множество | Бесконечное множество | Непустое множество | Пустое множество |
Множество звёзд во Вселенной; множество двоечников в классе; множество букв английского алфавита; фруктовых деревьев; множество чисел, которые делятся на нуль; множество съедобных грибов; множество натуральных чисел; множество домашних животных.
Имена объектов
Человек может сообщить самые разнообразные сведения о том или ином объекте. Но чтобы сделать это, нужно сначала как-то обозначить, выделить объект из ряда других объектов – дать ему имя.
Имя объекта люди называют, отвечая на вопрос что это такое? или кто это такой? Например, так: это – град, это – тетрадь, это – труд и т. д. Но в разных ситуациях один и тот же объект мы обозначаем разными именами. Например, собаку можно назвать Тузиком, пёсиком, щенком, другом человека или просто животным. Чем отличаются эти имена и от чего зависит выбор имени объекта в каждом случае?
Прежде всего, существуют имена общие и единичные. Общее имя обозначает множество объектов (страна, прозвище, планета), а единичное имя обозначает один конкретный объект в некотором множестве объектов (столица России, Александр Сергеевич Пушкин).
Имена также могут быть собственными и нарицательными. Собственные имена даются объектам только некоторых видов, например, людям (Александр Сергеевич Пушкин), домашним животным (Пушок), географическим объектам (Москва), планетам (Юпитер) и т. д. Нарицательные имена используются для называния целой группы объектов, например, человек, книга, лицо, буква. Вспомните, что в соответствии с правилами русского языка собственные имена вы пишете с прописной (заглавной) буквы, а нарицательные – со строчной.
Задания
1. Какие из нижеперечисленных имён объектов относятся к собственным именам, какие – к нарицательным?
Дуб, Византия, Урал, река, колодец, улица Почтовая, мультфильм «В стране невыученных уроков», Мухтар, облако, информатика.
2. Выделите на помещённом ниже рисунке два множества объектов. Дайте общее имя каждому множеству и единичное имя каждому объекту. Какие из выбранных вами имён будут являться собственными?
Признаки объектов
Признаком любого объекта может быть его свойство, действие, поведение или состояние.
Свойства объекта помогают описать его характеристики и возможности, то есть назвать отличительные признаки этого объекта. Например, в сообщении о черёмухе, взятом из ботанической энциклопедии, сказано: «Черёмуха обыкновенная – дерево или крупный кустарник высотой 0,6-10 м; крона удлинённая, густая, кора матовая, чёрно-серая, с беловатыми чечевичками; молодые ветви оливковые или вишнёво-красные; листья простые, очерёдные, яйцевидно-ланцетные или продолговато-эллиптические, длиной 3-15 см, тонкие, на коротких черешках, заострённые; цветки белые (реже розоватые), собраны в длинные густые поникающие кисти длиной 8-12 см, с сильным запахом, на цветоножках». Такое подробное описание свойств объекта помогает отличить объект «черёмуха» от других деревьев и кустарников.
Каждое свойство определяется некоторой величиной и её значением. Например, в описании черёмухи обыкновенной присутствуют такие величины, как высота, длина, цвет и форма. Значениями данных величин будут являться: 0,6-10 м, чёрно-серая, розоватые, матовая, удлинённая, продолговато-эллиптические и др.
Признаки (свойства) могут быть существенными – необходимыми, крайне важными для выделения данного объекта из множества других, похожих на него. Так, существенными признаки, которые помогают отличить карликовую берёзу от других видов берёз, являются малая высота (до 1,2 м), маленький размер листьев (от 5 мм до 1,5 см), кустарниковая форма, стелящиеся по земле побеги.
В таблице приведены характеристики объектов и величины, которыми эти свойства могут быть обозначены:
| Объект | Характеристика | Величина | Значение величины |
| Стол | Деревянный | Материал | Дерево |
| Стол | С тремя выдвижными ящиками | Количество выдвижных ящиков | 3 |
| Человек | Темноволосый | Цвет волос | Тёмный (чёрный) |
| Кошка | Породистая | Порода | Сиамская, египетская и т. д. |
| Монитор | Широкоформатный, с диагональю 23″ | Диагональ экрана монитора (дюймов) | 23 дюйма |
Имена действий обозначают процессы, которые могут происходить с объектом: «самолёт летает», «мяч отскакивает», «в записной книжке можно хранить номера телефонов». Имена действий также помогают подробно описать какой-либо объект.
Задание
Попробуйте обозначить характеристики приведённых ниже объектов, воспользовавшись школьными учебниками:
Множества,их элементы,поджмножества
Вы будете перенаправлены на Автор24
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
Обозначение множеств, подмножеств и их элементов
Готовые работы на аналогичную тему
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ <\rm :\ >54\in A.\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Например, рассмотрим множества
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Например, рассмотрим два множества:
Объединение множеств
Математически это можно обозначить так:$\ А\ \cup B$
Разность множеств
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 05 2021