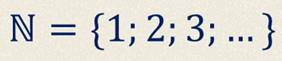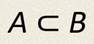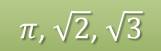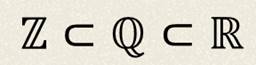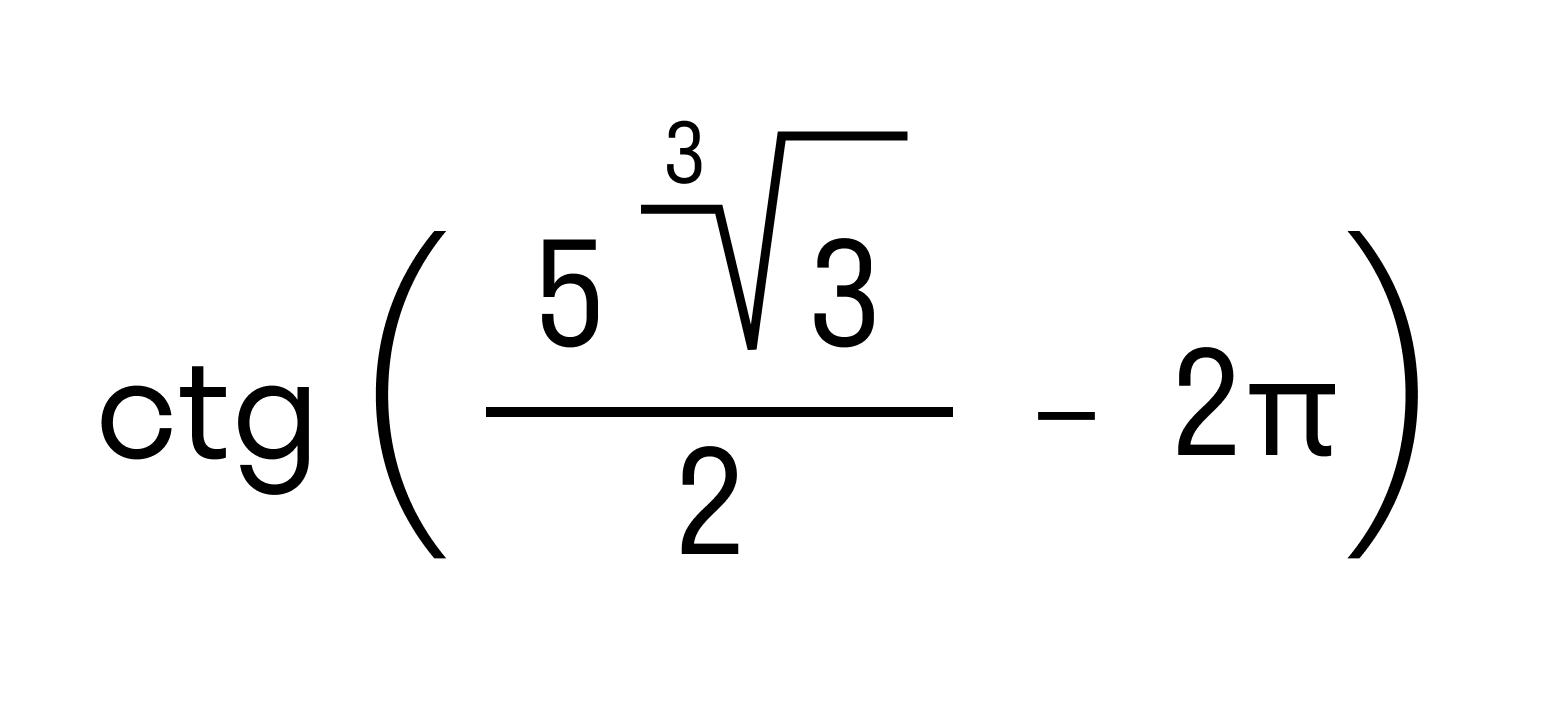Что называют множеством действительных чисел

Множество действительных чисел

Урок 5. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Множество действительных чисел»

· повторить все изученные ранее множества чисел;

· вспомнить, что множество действительных чисел является объединением множеств рациональных и иррациональных чисел;

· вспомнить, что множество рациональных чисел включает множество целых чисел и все дроби, кроме бесконечных непериодических.

Сначала вспомним, что понимают под словом множество в математике.

Множество — это совокупность некоторых объектов, объединённых по какому-либо признаку.

Приведём примеры множеств:

Множество принято обозначать заглавной латинской буквой.

Вы же помните, что множество чисел, которые используются для счёта, называют множеством натуральных чисел и обозначают буквой N.

Самое время, говоря о множестве натуральных чисел, вспомнить понятие числового множества.

Числовое множество – множество, элементами которого являются числа.

Элементы множества записывают в фигурных скобках. Так элементами множества натуральных чисел, являются числа 1, 2, 3 и так далее.

Множество А называют подмножеством множества B, если каждый элемент множества А является элементом множества B. Записываю это так.

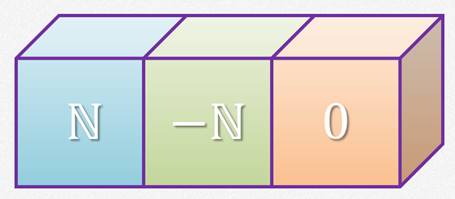
Мы с вами ранее говорили о множестве целых чисел. Оно состоит из натуральных чисел, чисел противоположных натуральным и нуля.

Хорошо видно, что каждый элемент множества натуральных чисел принадлежит множеству целых чисел. То есть множество N является подмножеством множества Z.

Сейчас вернёмся к одному из рассмотренных ранее способов представления обыкновенной дроби в виде десятичной.

Мы с свами при повторении этого вопроса рассматривали 3 примера, в которых получили конечную десятичную дробь и бесконечные периодические десятичные дроби.

Но вам известно ещё и о существовании бесконечных непериодических десятичных дробей.

Это бесконечная десятичная дробь, в которой нет периода. В качестве примера такой дроби можно привести хорошо известное вам число π.

Так множество бесконечных непериодических дробей составляет множество иррациональных чисел.

В свою очередь множество рациональных чисел содержит в себе множество целых чисел, конечных десятичных дробей и бесконечных периодических дробей.

Понятно, что любое целое число можно представить в виде обыкновенной дроби со знаменателем 1. Также вы знаете, как любую конечную десятичную дробь и любую бесконечную периодическую десятичную дроби можно представить в виде обыкновенной.

Тогда можно дать такое определение рациональному числу.

Рациональное число – число, которое можно представить в виде дроби, где числитель является целым числом, а знаменатель — натуральным.

Рациональные и иррациональные числа в совокупности составляют множество действительных чисел.

Из этих иллюстраций видно, что множество Z целых чисел является подмножеством множества рациональных чисел. А множество рациональных чисел является подмножеством множества действительных чисел.

И ранее мы говорили, что множество натуральных чисел является подмножеством множества целых чисел.

Мы говорили, что любую конечную десятичную дробь и любую бесконечную периодическую десятичную дроби всегда можно представить в виде обыкновенной.

С конечной десятичной дробью сложностей не должно возникать, мы на предыдущих уроках рассматривали такие случаи.

А вот правило обращения периодической десятичной дроби в обыкновенную стоит напомним. Рассмотрим его подробнее.

Выполним несколько заданий, где и применим знания о множествах чисел.

Теперь вернёмся к понятию множества и подробнее поговорим о пересечении и объединении множеств.

Объединением (или суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.

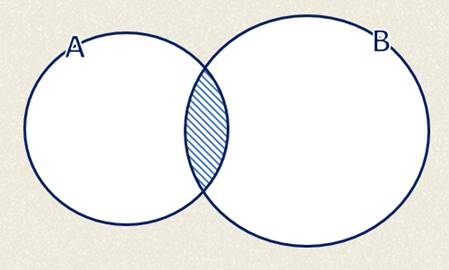
Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит и множеству А, и множеству В одновременно.

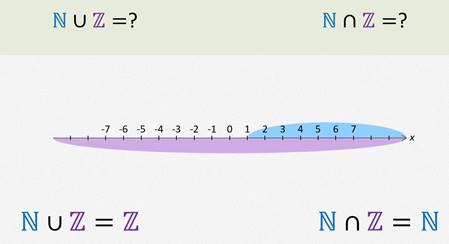
Пользуясь этими определениями найдём объединение и пересечение множеств натуральных и целых чисел.

Итак, пересечением данных множеств является множество натуральных чисел, а объединением — множество целых чисел.

Мы с вами повторили все изученные ранее множества чисел. Множество действительных чисел является объединением множеств рациональных и иррациональных чисел.

Множество рациональных чисел в свою очередь включает множество целых чисел и все дроби, кроме бесконечных непериодических, которые и составляют множество иррациональных чисел.

Ну, а в множество целых чисел входят натуральные, противоположные натуральным и 0.

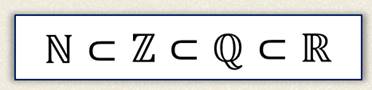
И справедлива такая запись, которая демонстрирует связь всех известных нам числовых множеств.

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

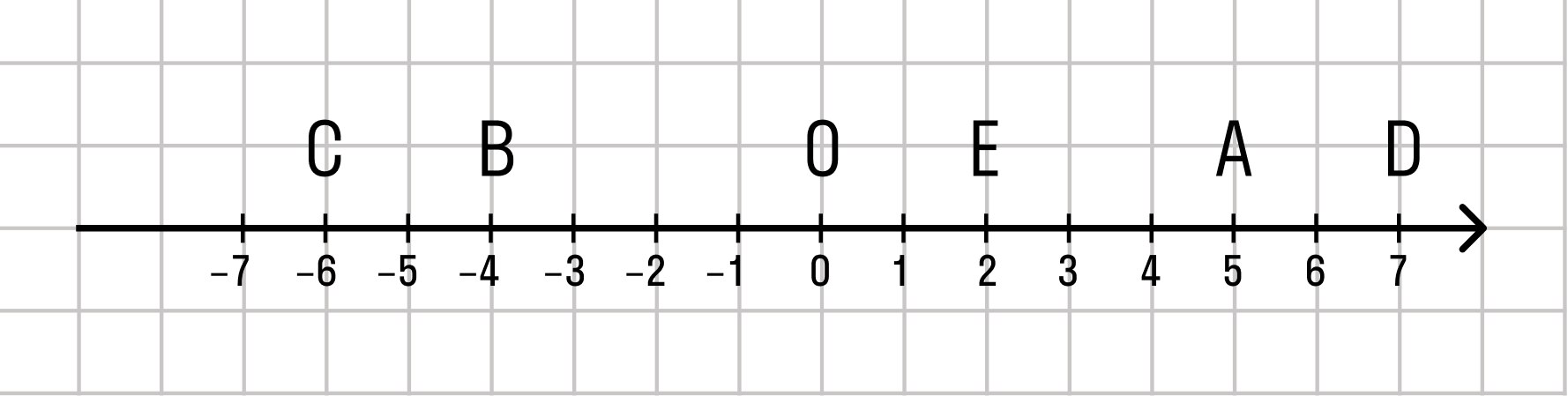
Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Числа. Действительные числа.

Вещественное, или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.

Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых иррациональные числа.

Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой. Вещественные числа состоят из простых объектов: целых и рациональных чисел.

Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.

Бесконечная десятичная дробь, это десятичная дробь, у которой после запятой есть бесконечное число цифр.

Числа, которые нельзя представить в виде , являются иррациональными числами.

Пример:

Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.

Рациональные и иррациональные числа создают множество действительных чисел. Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая.

Для числовых множеств используются обозначения:

Теория бесконечных десятичных дробей.

Вещественное число определяется как бесконечная десятичная дробь, т.е.:

где ± есть один из символов + или −, знак числа,

a₀ — целое положительное число,

a₁,a₂,…a_n,… — последовательность десятичных знаков, т.е. элементов числового множества <0,1,…9>.

Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:

Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно. Например, предположим даны 2 положительны числа:

Если a₀0, то α b₀ то α>β. Когда a₀=b₀ переходим к сравнению следующего разряда. И т.д. Когда α≠β, значит после конечного количества шагов встретится первый разряд n, такой что a_n≠b_n. Если a_nn, то α b_n то α>β.

Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например, суммой вещественных чисел α и β является вещественное число α+β, которое удовлетворяет таким условиям:

Аналогично определяет операция умножения бесконечных десятичных дробей.

Источник

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Числа. Действительные числа.

Вещественное, или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.

Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых иррациональные числа.

Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой. Вещественные числа состоят из простых объектов: целых и рациональных чисел.

Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.

Бесконечная десятичная дробь, это десятичная дробь, у которой после запятой есть бесконечное число цифр.

Числа, которые нельзя представить в виде , являются иррациональными числами.

Пример:

Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.

Рациональные и иррациональные числа создают множество действительных чисел. Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая.

Для числовых множеств используются обозначения:

Теория бесконечных десятичных дробей.

Вещественное число определяется как бесконечная десятичная дробь, т.е.:

где ± есть один из символов + или −, знак числа,

a₀ — целое положительное число,

a₁,a₂,…a_n,… — последовательность десятичных знаков, т.е. элементов числового множества <0,1,…9>.

Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:

Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно. Например, предположим даны 2 положительны числа:

Если a₀0, то α b₀ то α>β. Когда a₀=b₀ переходим к сравнению следующего разряда. И т.д. Когда α≠β, значит после конечного количества шагов встретится первый разряд n, такой что a_n≠b_n. Если a_nn, то α b_n то α>β.

Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например, суммой вещественных чисел α и β является вещественное число α+β, которое удовлетворяет таким условиям:

Аналогично определяет операция умножения бесконечных десятичных дробей.

Источник