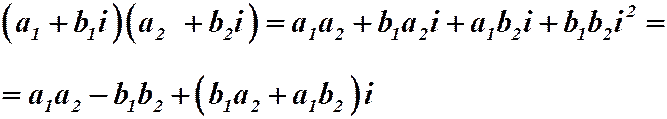Что называют мнимой единицей
Мнимая единица
Маяковский про мнимую единицу
Мнимая единица (讠, один с точечкой) — это:
Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.
Содержание
История открытия [ править ]
Основные свойства [ править ]
После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:
2 i = 2 i e e = 21 ⋅ e e = 21 <\displaystyle 2i=<\frac <2ie>
Тождество Эйлера [ править ]
Существует следующее тождество:
Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.
Доказательство [ править ]
e − i π ∗ e i π = ( − 1 ) ∗ ( − 1 ) <\displaystyle e^<-i\pi >*e^
В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!
Опровержение [ править ]
e i π + 1 = e 1 ⋅ π + 1 = e π + 1 ≠ 0 <\displaystyle e^
Опровержение опровержения [ править ]
Не верьте этому опровержению, Эйлер говорил правду. (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)
Следствие 1 [ править ]
Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:
Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:
Следствие 2 [ править ]
Еще раз рассмотрим вышеприведённое тождество Эйлера:
А теперь возведем обе его части в любую целую нечётную степень n:
А значит, при любом нечётном n,
Интересные факты [ править ]
Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует. i 2 = − 1 <\displaystyle i^<2>=-1> далее
В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы.
Мнимая единица
Мни́мая едини́ца — обычно комплексное число, квадрат которого равен −1 (минус единице). Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксону или в рамках алгебры по Клиффорду.
Содержание
Для комплексных чисел
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0 с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x^2 + 1 = 0 не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i через радикал (как \sqrt <-1>).
Определение
Мнимая единица — это число, квадрат которого равен −1. Т.е. i — это одно из решений уравнения
Степени мнимой единицы
Степени i повторяются в цикле:
Что может быть записано для любой степени в виде:
где n — любое целое число.
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i :
Корни из мнимой единицы
В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
Это следует из формулы Муавра и того, что мнимая единица может быть представлена в тригонометрическом виде:
Также корни из мнимой единицы могут быть представлены в показательном виде:
Иные мнимые единицы
К вопросу об интерпретации и названии
 | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. |
Обозначения
См.также
Напишите отзыв о статье «Мнимая единица»
Примечания
Ссылки
Отрывок, характеризующий Мнимая единица
В самом городе между тем было пусто. По улицам никого почти не было. Ворота и лавки все были заперты; кое где около кабаков слышались одинокие крики или пьяное пенье. Никто не ездил по улицам, и редко слышались шаги пешеходов. На Поварской было совершенно тихо и пустынно. На огромном дворе дома Ростовых валялись объедки сена, помет съехавшего обоза и не было видно ни одного человека. В оставшемся со всем своим добром доме Ростовых два человека были в большой гостиной. Это были дворник Игнат и казачок Мишка, внук Васильича, оставшийся в Москве с дедом. Мишка, открыв клавикорды, играл на них одним пальцем. Дворник, подбоченившись и радостно улыбаясь, стоял пред большим зеркалом.
– Вот ловко то! А? Дядюшка Игнат! – говорил мальчик, вдруг начиная хлопать обеими руками по клавишам.
– Ишь ты! – отвечал Игнат, дивуясь на то, как все более и более улыбалось его лицо в зеркале.
– Бессовестные! Право, бессовестные! – заговорил сзади их голос тихо вошедшей Мавры Кузминишны. – Эка, толсторожий, зубы то скалит. На это вас взять! Там все не прибрано, Васильич с ног сбился. Дай срок!
Игнат, поправляя поясок, перестав улыбаться и покорно опустив глаза, пошел вон из комнаты.
– Тетенька, я полегоньку, – сказал мальчик.
– Я те дам полегоньку. Постреленок! – крикнула Мавра Кузминишна, замахиваясь на него рукой. – Иди деду самовар ставь.
Мавра Кузминишна, смахнув пыль, закрыла клавикорды и, тяжело вздохнув, вышла из гостиной и заперла входную дверь.
Выйдя на двор, Мавра Кузминишна задумалась о том, куда ей идти теперь: пить ли чай к Васильичу во флигель или в кладовую прибрать то, что еще не было прибрано?
В тихой улице послышались быстрые шаги. Шаги остановились у калитки; щеколда стала стучать под рукой, старавшейся отпереть ее.
Мавра Кузминишна подошла к калитке.
– Кого надо?
– Графа, графа Илью Андреича Ростова.
– Да вы кто?
– Я офицер. Мне бы видеть нужно, – сказал русский приятный и барский голос.
Мавра Кузминишна отперла калитку. И на двор вошел лет восемнадцати круглолицый офицер, типом лица похожий на Ростовых.
– Уехали, батюшка. Вчерашнего числа в вечерни изволили уехать, – ласково сказала Мавра Кузмипишна.
Молодой офицер, стоя в калитке, как бы в нерешительности войти или не войти ему, пощелкал языком.
– Ах, какая досада. – проговорил он. – Мне бы вчера… Ах, как жалко.
Мавра Кузминишна между тем внимательно и сочувственно разглядывала знакомые ей черты ростовской породы в лице молодого человека, и изорванную шинель, и стоптанные сапоги, которые были на нем.
– Вам зачем же графа надо было? – спросила она.
– Да уж… что делать! – с досадой проговорил офицер и взялся за калитку, как бы намереваясь уйти. Он опять остановился в нерешительности.
– Видите ли? – вдруг сказал он. – Я родственник графу, и он всегда очень добр был ко мне. Так вот, видите ли (он с доброй и веселой улыбкой посмотрел на свой плащ и сапоги), и обносился, и денег ничего нет; так я хотел попросить графа…
Мавра Кузминишна не дала договорить ему.
Мнимая единица
Маяковский про мнимую единицу
Мнимая единица (讠, один с точечкой) — это:
Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.
Содержание
История открытия [ править ]
Основные свойства [ править ]
После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:
2 i = 2 i e e = 21 ⋅ e e = 21 <\displaystyle 2i=<\frac <2ie>
Тождество Эйлера [ править ]
Существует следующее тождество:
Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.
Доказательство [ править ]
e − i π ∗ e i π = ( − 1 ) ∗ ( − 1 ) <\displaystyle e^<-i\pi >*e^
В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!
Опровержение [ править ]
e i π + 1 = e 1 ⋅ π + 1 = e π + 1 ≠ 0 <\displaystyle e^
Опровержение опровержения [ править ]
Не верьте этому опровержению, Эйлер говорил правду. (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)
Следствие 1 [ править ]
Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:
Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:
Следствие 2 [ править ]
Еще раз рассмотрим вышеприведённое тождество Эйлера:
А теперь возведем обе его части в любую целую нечётную степень n:
А значит, при любом нечётном n,
Интересные факты [ править ]
Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует. i 2 = − 1 <\displaystyle i^<2>=-1> далее
В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы.
мнимая единица
Смотреть что такое «мнимая единица» в других словарях:
Мнимая единица — Мнимая единица обычно комплексное число, квадрат которого равен отрицательной единице. Однако возможны и иные варианты: в конструкции удвоения по Кэли Диксона или в рамках алгебр по Клиффорду. Содержание 1 Для комплексных чисел 1.1… … Википедия
МНИМАЯ ЕДИНИЦА — число i, квадрат которого равен отрицательной единице; т. о., i =. См. Комплексное число … Большой Энциклопедический словарь
Мнимая единица — число i, квадрат которого равен отрицательной единице; таким образом … Большая советская энциклопедия
МНИМАЯ ЕДИНИЦА — комплексное число i, квадрат к рого равен минус единице … Математическая энциклопедия
МНИМАЯ ЕДИНИЦА — число i, квадрат к рого равен отрицат. единице; т.о., i = корень из l. См. Комплексное число … Естествознание. Энциклопедический словарь
Единица — (един, один) многозначный термин. Нечто единое целое. Объект, обеспечивающий выполнение определённой функции, и который может быть заменён. Содержание 1 Математика 2 Измерение 3 Техни … Википедия
Единица (теория множеств) — Единица (един, один) многозначный термин. Содержание 1 Математика 2 Измерение 3 Экономика 4 Государство … Википедия
Мнимая часть — комплексного числа z = х + iy, множитель у при мнимой единице (См. Мнимая единица) i; М. ч. обозначается Im z … Большая советская энциклопедия
Степени мнимой единицы
Лекция 1. Комплексные числа.
Комплексные числа
Действительных чисел оказывается недостаточно для решения алгебраических уравнений.
Например: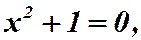 
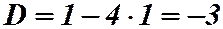
или 
; 
.
Для решения уравнения 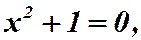нужно ввести некоторое новое число и считать его решением этого уравнения. Будем обозначать это новое число символом i.
Таким образом, для числа i справедливо (так как он корень уравнения):
— называется мнимой единицей; 
.
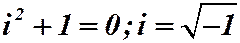
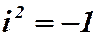
Введение мнимой единицы позволяет извлекать корни чётных степеней из отрицательных чисел.
Степени мнимой единицы
Рассмотрим степени мнимой единицы:
 |
 |
 |
 |
 |
 |
 |
 |
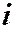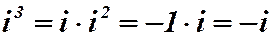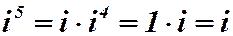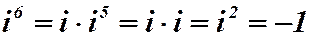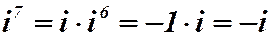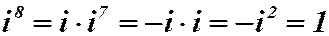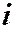
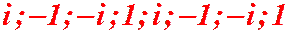
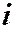
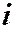
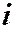
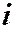
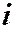
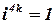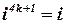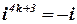Если выписать все значения степеней числа , то мы получим такую последовательность: 
и т.д. Легко видеть, что значения степеней числа повторяются с периодом равным четырём. Таким образом, если показатель степени числа делится на четыре, то значение степени равно 1; если при делении показателя степени на четыре в остатке получается 1, то значение степени равно ; если при делении показателя степени на четыре в остатке получается 2, то значение степени 
; если при делении показателя степени на четыре в остатке получается 3,то значение степени равно – . Пользуясь этим правилом можно вычислять любую степень числа .
 |
 |
 |
 |
Определение 1.1. Комплексными числами называются выражения вида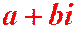 
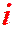
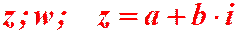
(а, b – действительные числа, 
– символ) и обозначаются: 
.
a– это действительная часть комплексного числа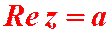 
,
b– это мнимая часть комплексного числа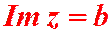 
.
Если 
, то комплексное число называется чисто мнимым, если 
, то комплексное число равно а, называется действительным.
Пример1.1.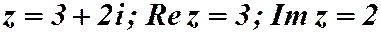 
.
.
.
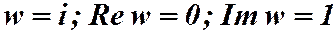
Для комплексных чисел вводятся понятия сложения, умножения и равенства:
а) Два комплексных числа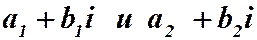 
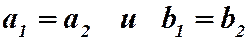
равны тогда и только тогда, когда 
.
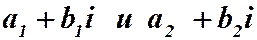
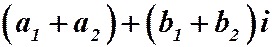
б) Суммой чисел называется число 
.
в) Произведением комплексных чисел – называется число: 
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.