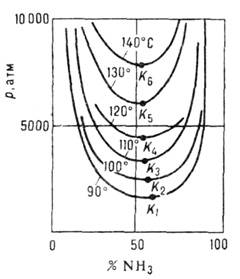
Что называют критическими точками
КРИТИЧЕСКАЯ ТОЧКА
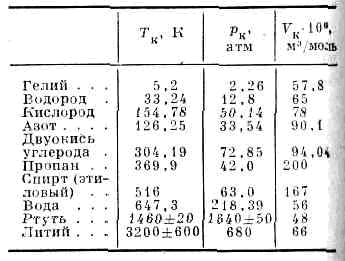
-точка на диаграмме состояния веществ, соответствующая критическому состоянию, в к-ром две (или более) фазы, находящиеся в термодинамич. равновесии, становятся тождественными по своим свойствам. В частности, с приближением к критическому состоянию различия в плотности, составе и др. свойствах сосуществующих фаз, а также теплота фазового перехода и межфазное поверхностное натяжение уменьшаются, а в К. т. равны нулю.
Критические параметры некоторых веществ
Диоксид углерода СО 2
Гексафторид серы SF 6
Триоксид серы SO 3
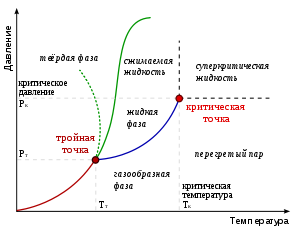
При темп-pax выше Т с возможен непрерывный (без фазового превращения) переход вещества из газообразного состояния в жидкое, поэтому К. т. является конечной точкой линии двухфазного равновесия.
Переход системы из однофазного состояния в двухфазное вне К. т. и изменение состояния в самой К. т. существенно различаются. В первом случае при расслаивании на две фазы переход начинается с появлением небольшого кол-ва (зародыша) 2-й фазы, свойства к-рой отличаются от свойств 1-й фазы, что сопровождается выделением или поглощением теплоты фазового перехода. Поскольку возникновение зародыша новой фазы приводит к появлению поверхности раздела фаз и поверхностной энергии, для его рождения требуется определ. энергия. Это означает, что такой фазовый переход (1-го рода) может начаться лишь при нек-ром переохлаждении (перегреве) вещества, способствующем появлению устойчивых зародышей новой фазы (см. Кинетика фазовых переходов).
К. т. обнаруживает глубокую аналогию с точками фазовых переходов 2-го рода: в К. т. фазовый переход происходит в масштабах всей системы, а свойства флуктуационно возникающей новой фазы бесконечно мало отличаются от свойств исходной фазы. Поэтому возникновение новой фазы не связано с поверхностной энергией, т. е. исключается перегрев (переохлаждение), и фазовый переход не сопровождается выделением или поглощением теплоты, что характерно для фазовых переходов 2-го рода. Как и вблизи фазовых переходов 2-го рода, вблизи К. т. наблюдается ряд особенностей в поведении физ. свойств, обусловленных аномальным ростом флуктуации.
Лит. см. в ст. Критические явления. М. А. Анисимов.
Критическая точка (термодинамика)
| Фазовые переходы |
|---|
 |
| Статья является частью серии «Термодинамика». |
| Понятие фазы |
| Равновесие фаз |
| Квантовый фазовый переход |
| Разделы термодинамики |
| Начала термодинамики |
| Уравнение состояния |
| Термодинамические величины |
| Термодинамические потенциалы |
| Термодинамические циклы |
| Фазовые переходы |
| править |
| См. также «Физический портал» |
Критическая точка — сочетание значений температуры 
и давления 
(или, что эквивалентно, молярного объёма 
), при которых исчезает различие в свойствах жидкой и газообразной фаз вещества.
Критическая температура фазового перехода — значение температуры в критической точке. При температуре выше критической температуры газ невозможно сконденсировать ни при каком давлении.
Физическое значение
В критической точке плотность жидкости и её насыщенного пара становятся равны, а поверхностное натяжение жидкости падает до нуля, потому исчезает граница раздела фаз жидкость-пар.
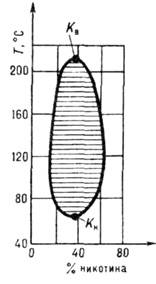
Для смеси веществ критическая температура не является постоянной величиной и может быть представлена пространственной кривой (зависящей от пропорции составляющих компонентов), крайними точками которой являются критические температуры чистых веществ — компонентов рассматриваемой смеси.
Критической точке на диаграмме состояния вещества соответствуют предельные точки на кривых равновесия фаз, в окрестностях точки фазовое равновесие нарушается, происходит потеря термодинамической устойчивости по плотности вещества. По одну сторону от критической точки вещество однородно (обычно при 
T_
В окрестностях точки наблюдаются критические явления: из-за роста характеристических размеров флуктуаций плотности резко усиливается рассеяние света при прохождении через вещество — при достижении размеров флуктуаций порядков сотен нанометров, т. е. длин волн света, вещество становится непрозрачным — наблюдается его критическая опалесценция. Рост флуктуаций приводит также к усилению поглощения звука и росту его дисперсии, изменению характера броуновского движения, аномалиям вязкости, теплопроводности, замедлению установления теплового равновесия и т. п.
История
Практически явление критической точки было обнаружено при нагревании жидкости, частично заполняющей запаянную трубку. По мере нагрева мениск постепенно терял свою кривизну, становясь всё более плоским, а при достижении критической температуры переставал быть различимым.
| Вещество | | | |
|---|---|---|---|
| Единицы | Кельвины | Атмосферы | см³/моль |
| Водород | 33,0 | 12,8 | 61,8 |
| Кислород | 154,8 | 50,1 | 74,4 |
| Ртуть | 1750 | 1500 | 44 |
| Этанол | 516,3 | 63,0 | 167 |
| Диоксид углерода | 304,2 | 72,9 | 94,0 |
| Вода | 647 | 218,3 | 56 |
| Азот | 126.25 | ||
| Аргон | 150.86 | ||
| Бром | 588 | ||
| Гелий | 5.19 | ||
| Йод | 819 | ||
| Криптон | 209.45 | ||
| Ксенон | 289.73 | ||
| Мышьяк | 1673 | ||
| Неон | 44.4 | ||
| Радон | 378 | ||
| Селен | 1766 | ||
| Сера | 1314 | ||
| Фосфор | 994 | ||
| Фтор | 144.3 | ||
| Хлор | 416.95 |
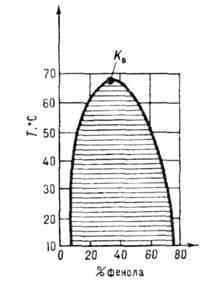
Критические точки существуют не только для чистых веществ, но и, в некоторых случаях, для их смесей и определяют параметры потери устойчивости смеси (с разделом фаз) — раствор (одна фаза). Примером такой смеси может служить смесь фенол-вода.
Критическая точка
Полезное
Смотреть что такое «Критическая точка» в других словарях:
КРИТИЧЕСКАЯ ТОЧКА — точка на диаграмме состояния, соответствующая критическому состоянию. К. т. двухфазного равновесия жидкость пар явл. конечной точкой на кривой испарения и характеризуется критич. значениями темп ры Tк, давления рк и объёма Vк (табл.). ПАРАМЕТРЫ… … Физическая энциклопедия
Критическая точка — Критическая точка многозначный термин: Критическая точка (математика) точка, где производная равна нулю, либо неопределена. Критическая точка (термодинамика) температура, при которой две фазы находятся в равновесии. Критическая… … Википедия
КРИТИЧЕСКАЯ ТОЧКА — изображает на диаграммах состояния критическое состояние вещества. Критическая точка заканчивается, напр., кривая фазового равновесия жидкость пар в системе координат: температура T, давление p … Большой Энциклопедический словарь
КРИТИЧЕСКАЯ ТОЧКА — предельная точка на кривой (см.) равновесия фаз системы, напр. жидкость пар, в которой исчезает различие между жидкостью и паром, а точка соответствует (см.) … Большая политехническая энциклопедия
критическая точка — Точка на термодинамической диаграмме, соответствующая критическому состоянию вещества. [Сборник рекомендуемых терминов. Выпуск 103. Термодинамика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики термодинамика… … Справочник технического переводчика
КРИТИЧЕСКАЯ ТОЧКА — КРИТИЧЕСКАЯ ТОЧКА, температура и давление, при превышении которых становится невозможным дальнейшее совместное существование жидкости и ее пара (или газа). Если газ медленно сжимать при температурах, превышающих критическую, или охлаждать при… … Научно-технический энциклопедический словарь
критическая точка — [critical point] критическая точка A1 [A1 critical point] температура превращения перлита ↔ аустенит в равновесной системе Fe Fe3C; критическая точка A2 [А2 critical point] температура, соответствующая точке Кюри феррита; критическая точка A3 [A3 … Энциклопедический словарь по металлургии
критическая точка — 3.2 критическая точка (critical point): Точка на кривой зависимости деформации образца от силы, в которой прямая, касательная к этой кривой, расходится с ней (см. рисунок 4а). Источник … Словарь-справочник терминов нормативно-технической документации
критическая точка — изображает на диаграммах состояния критическое состояние вещества; ею заканчивается, например, кривая фазового равновесия жидкость пар в системе координат: температура давление. * * * КРИТИЧЕСКАЯ ТОЧКА КРИТИЧЕСКАЯ ТОЧКА, изображает на… … Энциклопедический словарь
Критическая точка — Critical point Критическая точка. (1) Температура или давление, при которых возникают изменения в кристаллической структуре, фазе, физических свойствах. Также называемая температу рой превращения. (2) В диаграмном равновесии сочетание состава… … Словарь металлургических терминов
критическая точка — kritinis taškas statusas T sritis automatika atitikmenys: angl. critical point vok. kritischer Punkt, m rus. критическая точка, f pranc. point critique, m … Automatikos terminų žodynas
Критическая точка (термодинамика)
Из Википедии — свободной энциклопедии
 Внешние изображения | |
|---|---|
 | 1 Критическая кривая для системы пропан — изопентан [1] |
| 2 Кривая расслоения в системе с нижней критической точкой вода — 4-метил-3-этилпиридин, в которой достижению верхней критической точки препятствует кипение смеси [2] |
| 3 Примеры сложных фазовых диаграмм с верхней и нижней критическими точками расслоения [3] |
| 4 Критическая кривая расслоения k1K в системе из трёх жидкостей, две из которых ограниченно растворяются друг в друге [4] |
| 5 Пример критической кривой на пространственной диаграмме состояния [5] |
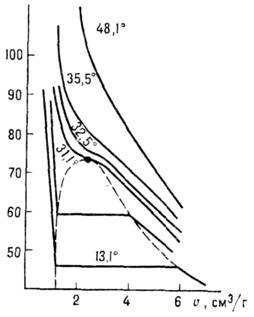
Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния.
где ρcrit — критическая плотность вещества, г/см³; M — молярная масса вещества, г/моль; Vcrit — критический удельный объём вещества, см³/моль.
При температуре выше критической газ невозможно перевести в жидкое состояние ни при каком давлении.
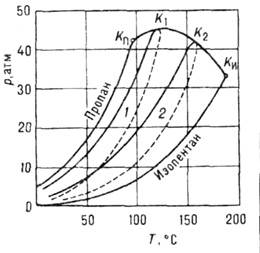
У смесей или растворов следует различать критическую точку равновесия жидкость — пар и критическую точку равновесия фаз различного состава, находящихся в одном агрегатном состоянии (жидкость — жидкость, газ — газ). В связи с этим критическая точка смесей (растворов) дополнительно характеризуется критической концентрацией компонентов. В результате увеличения числа параметров, определяющих состояние системы, у смесей имеется не одна критическая точка, а совокупность критических точек, образующих кривую критических точек [6] (критическую кривую [7] [8] ). Пример такой кривой приведён на внешнем изображении 1.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 
из этого промежутка выполняется неравенство 
. Другими словами – большему значению аргумента соответствует большее значение функции.
Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
.
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 
из этого промежутка выполняется неравенство 
. Другими словами – большему значению аргумента соответствует большее значение функции.
Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
5) Сделать выводы о монотонности функции и точках ее
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
Примеры и разбор решения заданий тренировочного модуля
Решение: Найдем производную заданной функции: у’=2x-8
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции: 
Найдем нули производной: 
Определим знаки производной функции и изобразим на рисунке поведение функции:
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 м\c
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3