Что называют истинной погрешностью
О погрешностях измерений



Виды измерений физических величин и их погрешностей
При измерении любой физической величины получить её абсолютно точное (истинное) значение невозможно из-за присутствующих всегда погрешностей измерений.
Различают прямые и косвенные измерения.
Измерение называютпрямым, если значение измеряемой величины (например, длины или массы предмета) находят в результате сравнения с мерой этой же величины (измерительной линейкой, гирями определенной массы) или считываются со шкалы прибора, используемого для проведения наблюдения (например, вольтметра при измерении электрического напряжения).
Измерение называюткосвенным, если значение измеряемой величины находят с помощью известной функциональной зависимости, которая связывает искомую величину с величинам, получаемыми непосредственно при прямых измерениях (например, сила электрического тока находится с помощью закона Ома по прямым измерениям электрического напряжения и сопротивления).
Все возможные погрешности измерений по характеру происхождения разделяют на три типа:
1. Грубая погрешность (промах) – чрезмерно большая погрешность, явно искажающая результат измерения.
Существует строгий математический способ определения ошибок подобного рода. Если подозрительное значение отличается от среднего более чем на 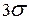
Эта погрешность, связанная с невнимательностью или ошибкой экспериментатора, исключается из протокола измерений. Имеет смысл измерение повторить.
2. Систематическая погрешность – погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.
Эта погрешность связана со сдвигом измеренного значения некоторой величины от её истинного значения. Если удается обнаружить причину или найти величину сдвига, то систематическую погрешность можно исключить введением поправки к измеренному значению величины. Однако, не существует универсальных правил, позволяющих найти систематическую погрешность данного измерения.
3. Случайные погрешности – погрешности, появление которых не может быть предупреждено.
Эти погрешности проявляются в разбросе отсчетов при повторных измерениях, проведенных в одних и тех же доступных контролю условиях, т.к. обусловлены факторами, меняющимися от измерения к измерению, действие которых на практике не всегда может быть учтено.
Выполнив измерение физической величины несколько раз, используя теорию погрешностей измерений, можно дать количественную оценку случайной погрешности и указать вероятность, с которой истинное значение измеряемой величины находится внутри некоторого интервала.
Методика статистической обработки результатов прямых измерений
Обозначим через 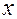
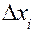
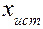
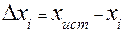
Поскольку, 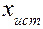
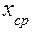
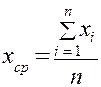
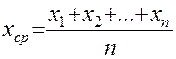
Тогда, ошибка отдельного измерения ( 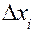
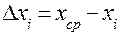
Зная ошибку каждого измерения, следующим шагом найдем, так называемоесреднеквадратическое отклонение среднего 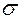
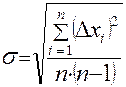
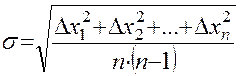
(Внимание! Среднеквадратическое отклонение среднего 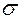
Формула для вычисления 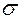
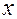
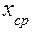
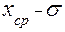
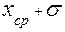
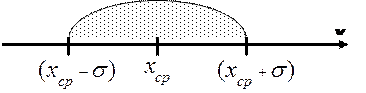 |
Оказывается, что при проведении новых серий экспериментов, следующие средние значения 
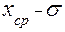
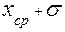
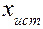
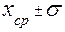
Вероятность 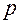
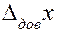
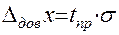
Обработка случайных погрешностей прямых измерений сводится к нахождению 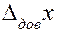
В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым 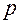
Таблица коэффициентов Стьюдента
для доверительной вероятности 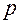
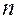 | ||||||
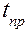 | 12,3 | 4,3 | 3,18 | 2,78 | 2,6 | 2,26 |
Полная погрешность измерений 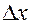
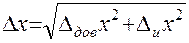
Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:
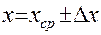
Рядом необходимо указать относительную погрешность
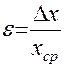
выраженную в процентах ( 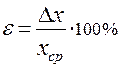
(Внимание! относительная погрешность ε превышающая 10%-15% свидетельствует о недостаточном усердии учащегося при выполнении лабораторной работы).
Заметим, что 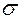
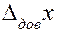
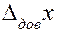
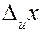
Величину случайной погрешности можно уменьшить многократным повторением измерения. Использование теории случайных погрешностей оправдано лишь в том случае, если повторные измерения дают результаты, заметно отличающиеся друг от друга.
О точности измерительных приборов
Развитие измерительной техники привело к появлению разнообразных приборов, отличающихся своей точностью.
Точность прибора – это свойство измерительного прибора, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины.
Точность прибора либо задается классом точности[1] прибора, либо указана в паспорте, прилагаемом к прибору. Погрешность, вносимая прибором при каждом отдельном измерении (приборная погрешность, Δхпр.), связана с точностью прибора. Эта погрешность равна той доле деления шкалы прибора, до которой с уверенностью в правильности результата можно производить отсчет.
В тех случаях, когда класс точности не указан и нет указаний в паспорте прибора, приборная погрешность принимается равной половине цены наименьшего деления шкалы прибора: Δхпр. = ± 0,5C, где С – цена наименьшего деления шкалы прибора.
В том случае, когда приборная и случайная погрешности сравнимы по величине, полную погрешность измерений можно представить в виде суммы двух составляющих: Δх = Δхслуч. + Δхпр..
Точность прибора невозможно превзойти никаким методом измерения на нем. Для более точных измерений применяют приборы более высокого класса.
Погрешности измерений и их классификация. Лекция
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
При измерении физических величии с помощью даже самых точных и совершенных средств и методов их результат всегда отличается от истинного значения измеряемой физической величины, т.е. определяется с некоторой погрешностью. Источниками погрешностей измерения являются следующие причины: несовершенство используемых методов и средств измерений, нестабильность измеряемых физических величин, непостоянство климатических условий, внешние и внутренние помехи, а также различные субъективные факторы экспериментатора.
Определение «погрешность» является одним из центральных в метрологии, в котором используются понятия «погрешность результата измерения» и «погрешность средства измерения».
Погрешностью результата измерения (погрешностью измерения) называется отклонение результата измерения от истинного значения измеряемой физической величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины.
Это значение находится экспериментальным путем и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него.
По способу количественного выражения погрешности измерения делятся на абсолютные, относительные и приведенные.
и знак полученной погрешности, но не определяет качество самого проведенного измерения.
Понятие погрешности характеризует как бы несовершенство измерения. Характеристикой качества измерения является используемое в метрологии понятие точности измерений, отражающее меру близости результатов измерений к истинному значению измеряемой физической величины. Точность и погрешность связаны обратной зависимостью. Иначе говоря, высокой точности измерений соответствует малая погрешность. Так, например, измерение силы тока в 10 А и 100 А может быть выполнено с идентичной абсолютной погрешностью ∆ = ±1 А. Однако качество (точность) первого измерения ниже второго. Поэтому, чтобы иметь возможность сравнивать качество измерений, введено понятие относительной погрешности.
Относительной погрешностью δ называется отношение абсолютной погрешности измерения к истинному значению измеряемой величины:
 |
Мерой точности измерений служит величина, обратная модулю относительной погрешности, т.е. 1/|δ|. Погрешность δ часто выражают в процентах:
δ = 100 △ /хн (%). Поскольку обычно △⋍ хн, то относительная погрешность может быть определена как δ ⋍ △ /х или δ = 100 △ /х (%).
Если измерение выполнено однократно и за абсолютную погрешность результата измерения △ принята разность между показанием прибора и истинным значением измеряемой величины хН то из соотношения (1.2) следует, что значение относительной погрешности δ уменьшается с ростом величины хн (здесь предполагается независимость △ от хн ). Поэтому для измерений целесообразно выбирать такой прибор, показания которого были бы в последней части его шкалы (диапазона измерений), а для сравнения различных приборов использовать понятие приведенной погрешности.
Приведенной погрешностью δпр, выражающей потенциальную точность измерений, называется отношение абсолютной погрешности △ к некоторому нормирующему значению XN (например, к конечному значению шкалы прибора или сумме конечных значений шкал при двусторонней шкале).
По характеру (закономерности) изменения погрешности измерений подразделяются на систематические, случайные и грубые (промахи).
• возможна их коррекция поправками только в данный момент времени, а далее эти погрешности вновь непредсказуемо изменяются;
• изменения прогрессирующих погрешностей во времени представляют собой нестационарный случайный процесс (характеристики которого изменяются во времени), и поэтому в рамках достаточно полно разработанной теории стационарных случайных процессов они могут быть описаны лишь с некоторыми ограничениями.
Грубые погрешности (промахи) — погрешности, существенно превышающие ожидаемые при данных условиях измерения. Такие погрешности возникают из-за ошибок оператора или неучтенных внешних воздействий. Их выявляют при обработке результатов измерений и исключают из рассмотрения, пользуясь определенными правилами.
По причинам возникновения погрешности измерения подразделяются на методические, инструментальные, внешние и субъективные.
Методические погрешности возникают обычно из-за несовершенства метода измерений, использования неверных теоретических предпосылок (допущений) при измерениях, а также из-за влияния выбранного средства измерения на измеряемые физические величины. При подключении электроизмерительного прибора от источника сигнала потребляется некоторая мощность. Это приводит к искажению режима работы источника сигнала и вызывает погрешность метода измерения (методическую погрешность).
Инструментальные (аппаратурные, приборные) погрешности возникают из-за несовершенства средств измерения» т.е. из-за погрешностей средств измерений. Источниками инструментальных погрешностей могут быть, например, неточная градуировка прибора и смещение нуля, вариация показаний прибора в процессе эксплуатации и т.д. Уменьшают инструментальные погрешности применением более точного прибора.
Субъективные погрешности вызываются ошибками оператора при отсчете показаний средств измерения (погрешности от небрежности и невнимания оператора, от параллакса, т.е. от неправильного направления взгляда при отсчете показаний стрелочного прибора и пр.). Подобные погрешности устраняются применением современных цифровых приборов или автоматических методов измерения.
По характеру поведения измеряемой физической величины в процессе измерений различают статические и динамические погрешности.
Статические погрешности возникают при измерении установившегося значения измеряемой величины, т.е. когда эта величина перестает изменяться во времени.
Динамические погрешности имеют место при динамических измерениях, когда измеряемая величина изменяется во времени и требуется установить закон ее изменения. Причина появления динамических погрешностей состоит в несоответствии скоростных (временных) характеристик прибора и скорости изменения измеряемой величины.
Средства измерений могут применяться в нормальных и рабочих условиях.
Эти условия для конкретных видов СИ ( средств измерения ) установлены в стандартах или технических условиях.
Нормальным условиям применения средств измерений должен удовлетворять ряд следующих (основных) требований:
температура окружающего воздуха (20±5) °С;
относительная влажность (65±15) %;
атмосферное давление (100±4) кПа;
напряжение питающей сети (220±4) В и (115±2,5) В;
частота сети (50±1) Гц и (400±12) Гц.
Как следует из перечисленных требований, нормальные условия применения СИ характеризуются диапазоном значений влияющих на них величин типа климатических факторов и параметров электропитания.
Рабочие условия применения СИ определяются диапазоном значений влияющих величин не только климатического характера и параметров электропитания, но и типа механических воздействий. В частности, диапазон климатических воздействий делится на ряд групп, охватывающих широкий диапазон изменения окружающей температуры.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Погрешность измерений. Классификация
Погрешность средств измерения и результатов измерения.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.
Статическая и динамическая погрешности.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Систематическая и случайная погрешности.
Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.
Причинами возникновения систематических составляющих погрешности измерения являются:
Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.
Погрешности адекватности и градуировки.
Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.
Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.
Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.
Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.
Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
Аддитивные и мультипликативные погрешности.
Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:
– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).



