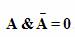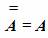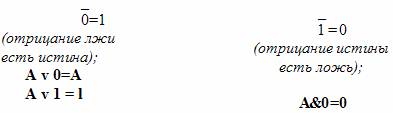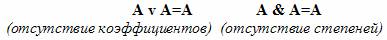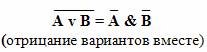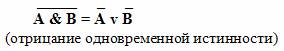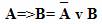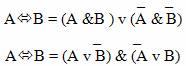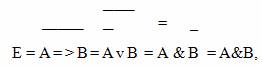Что называют формулами алгебры логики

10.04.202214.04.2022 admin 0 Comments

Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.

Что такое алгебра и алгебра логики

Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.

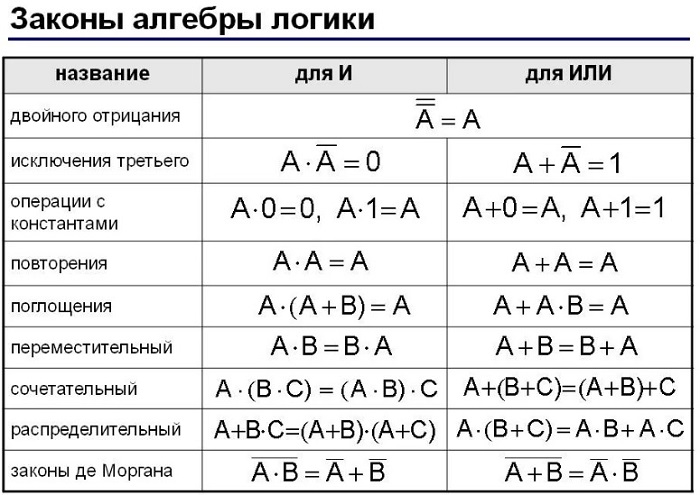
Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

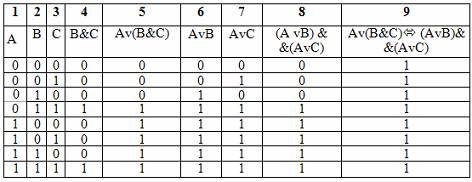
Основные законы алгебры логики представлены в таблице:

Логические выражения

В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.

Нью-Йорк — столица США (ложное);

в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.

Идёт дождь, а у меня нет зонта.

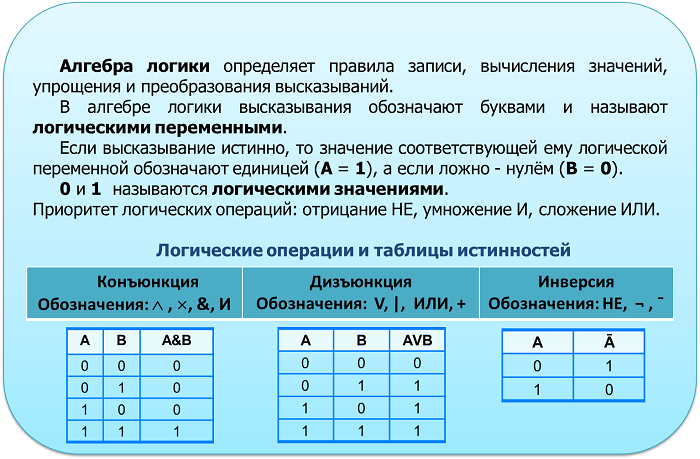
Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

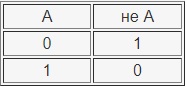
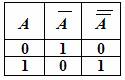
Логическое отрицание (инверсия) —НЕ

Таблица истинности инверсии:

Результаты операции НЕ следующие:

если исходное выражение истинно, то результат его отрицания будет ложным;

если исходное выражение ложно, то результат его отрицания будет истинным.

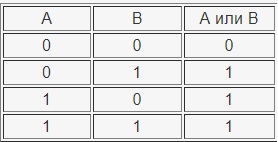
Логическое сложение (дизъюнкция, объединение) — ИЛИ

Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.

Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.

Таблица истинности операции ИЛИ:

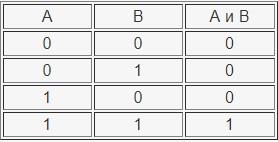
Логическое умножение(конъюнкция) — И

В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).

При всех остальных значениях операция будет ложной.

Таблица истинности операции И приведена ниже:

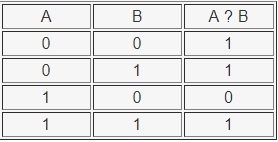
Логическое следование (импликация) — ЕСЛИ ТО

Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если. то».

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.

Таблица истинности операции ЕСЛИ ТО выглядит так:

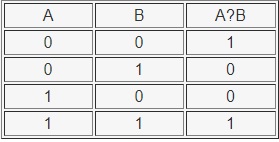
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

Таблица истинности операции эквивалентности:

Источник

Основы алгебры логики

Основные законы алгебры логики.

Законы алгебры высказываний

Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.

Законы алгебры высказываний (алгебры логики) — это тавтологии.

Иногда эти законы называются теоремами.

В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.

Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.

Закон тождества:

Всякое понятие и суждение тождественно самому себе.

Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.

Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, теперь смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия.

В рассуждении: Движение вечно. Хождение в школу — движение. Следовательно, хождение в школу вечно слово «движение» используется в двух разных смыслах (первое — в философском смысле — как атрибут материи, второе — в обыденном смысле — как действие по перемещению в пространстве), что приводит к ложному выводу.

Закон непротиворечия :

В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:

1. Число 12345 либо четное, либо нечетное, третьего не дано.

2. Предприятие работает убыточно или безубыточно.

3. Эта жидкость является или не является кислотой.

Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: « либо — либо », « истина—ложь ». Там же, где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.

Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.

Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.

По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.

Таким образом, мы можем сформулировать закон двойного отрицания:

Аналогичным образом можно вывести и проверить следующие законы:

Свойства констант:

Законы идемпотентности:

Законы коммутативности:

Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.

Законы ассоциативности:

A v(B v C) = (A v B) v C;

Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.

Законы дистрибутивности:

A v (B & C) = (A v B) &(A v C)

(дистрибутивность дизъюнкции
относительно конъюнкции)

А & (B v C) = (A & B) v (А & C)

(дистрибутивность конъюнкции
относительно дизъюнкции)

Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:

Законы поглощения:

Проведите доказательство законов поглощения самостоятельно.

Законы де Моргана:

Словесные формулировки законов де Моргана:

Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.

Примеры выполнения закона де Моргана:

1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.

2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.

Замена операций импликации и эквивалентности

Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.

Так, заменить операцию импликации можно в соответствии со следующим правилом:

Для замены операции эквивалентности существует два правила:

В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.

Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.

Рассмотрим следующий пример.

Пусть дано высказывание:

Источник

Тема 2 Формулы алгебры логики

2.1 Равносильные формулы алгебры логики

2.2 Законы алгебры логики

Как и в элементарной математике из «элементарных» булевых функций с помощью логических операций можно строить формулы. В настоящем разделе изучаются формулы алгебры логики.

2.1 Равносильные формулы алгебры логики. Приведем определение формулы алгебры логики.

1) каждая «элементарная» булева функция – формула;

2) если некоторое выражение N есть формула, то тоже формула;

3) если некоторые выражения M и N есть формулы, то выражения , , , тоже формулы;

4) других формул, кроме построенных по п. п.1), 2), 3), нет.

Формулы алгебры логики мы будет обозначать большими N, M, … Например, следующие выражения являются формулами алгебры логики:

, .

С целью упрощения формул, условимся, что операция конъюнкции «сильнее» операции дизъюнкции, импликации и эквивалентности, т. е. если нет скобок, то вначале выполняется операция конъюнкции.

Формула алгебры логики определяет некоторую булеву функцию, значение которой совпадает со значениями данной формулы для всех наборов значений переменных.

Две формулы N и M называются Равносильными, если они определяют одну и ту же булеву функцию (запись N=M будет означать, что формулы N и M равносильны).

Пример 1. Формулы и равносильны, т. е. .

Действительно, построим таблицы истинности для данных формул.

Из таблицы видно, что формулы и определяют одну и ту же булеву функцию и, следовательно, являются равносильными.

Очевидно, что отношение равносильности формул алгебры логики является:

1. рефлексивным, т. е. N=N для любой формулы N;

2. симметричным, т. е. если N=M, то M=N для любых формул N и M;

3. транзитивным, т. е. если N=M и M=J, то N=J для любых формул N, M,J.

Таким образом, отношение равносильности является отношением эквивалентности.

Если какую-нибудь формулу N1, являющуюся частью формулы N заменить формулой N2, равносильной N1, то полученная формула окажется равносильной N. Это свойство лежит в основе преобразования формул с целью их упрощения или приведения к определенной форме.

При преобразовании формул алгебры логики используются свойства логических операций, которые будут рассмотрены ниже.

2.2 Законы алгебры логики. Приведем перечень важнейших равносильностей (законов) алгебры логики. Эти равносильности выражают свойства логических операций.

1. — закон тождества;

2. — закон противоречия;

3. — закон исключительного третьего;

4. — закон двойного отрицания;

5. , — законы идемпотентности;

6. , — законы коммутативности;

7. , — законы дистрибутивности;

8. , — законы ассоциативности;

9. , — законы де Моргана;

10. ,

11. ,

12. , — законы поглощения;

13. , — законы склеивания.

Перечисленные законы алгебры логики доказываются с помощью таблицы истинности. В качестве примера докажем справедливость закона .

Из таблицы видно, что формулы и определяют одну и ту же булеву функцию. Следовательно, они равносильны.

Логические операции – конъюнкция, дизъюнкция, импликация и эквивалентность, вообще говоря, не являются независимыми друг от друга. В самом деле,

Первые две равносильности легко доказываются с помощью таблиц истинности. Две последние равносильности докажем с помощью законов де Моргана и двойного отрицания:

; .

Итак, справедливы следующие утверждения:

1) импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание;

2) конъюнкцию можно выразить через дизъюнкцию и отрицание;

3) дизъюнкцию можно выразить через конъюнкцию и отрицание;

4) все операции посредством равносильных выражений можно заменить двумя: конъюнкцией и отрицанием или дизъюнкцией и отрицанием.

Естественно возникает следующий вопрос. Для чего вводить пять логических операций, когда можно обойтись двумя? Использование лишь двух операций существенным образом усложнило бы запись, что привело бы к громоздким формулам. Однако в некоторых приложениях математической логики удобно ограничиться двумя операциями. Аналогичная ситуация имеет место в арифметике. Всякое натуральное число можно записать с помощью цифр 0 и 1. Однако записи чисел и выкладки в двоичной системе громоздки. К этой системе прибегают лишь в некоторых случаях.

Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют Булевой алгеброй. Законы 1-13 являются Основными законами булевой алгебры.

Обратим внимание на характер соответствий между равносильностями, объединенными в пару под номерами (5-13). В этих соответствиях проявляется так называемый закон двойственности.

Назовем формулу алгебры логики Двойственной к формуле , если =.

Будем говорить, что операция конъюнкции двойственна операции дизъюнкции и наоборот.

Как показано в пункте 2.2, всякая формула алгебры логики может быть приведена равносильными преобразованиями к формуле, содержащей только операции конъюнкции, дизъюнкции и отрицания. Поэтому, учитывая законы де Моргана и двойного отрицания, две формулы алгебры логики N и M, содержащие только операции конъюнкции, дизъюнкции и отрицания, будут двойственными, если одна получается из другой заменой каждой операции на двойственную и 1 заменяется на 0, а 0 на 1.

Например, формула двойственная к формуле , а формула двойственная к формуле .