Что называют доверительным интервалом
Доверительные интервалы
Определение
Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.
Нормальное распределение
Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.
Формула
Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула
где X – математическое ожидание выборки, α – уровень статистической значимости, Zα/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.
Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде
Пример
Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Zα/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят
А сам доверительный интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.
Методы сужения доверительного интервала
Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.
Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Zα/2=1,64. В этом случае нижняя и верхняя граница интервала составят
А сам доверительный интервал может быть записан в виде
В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].
Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов
Сам доверительный интервал станет иметь следующий вид
Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.
Построение доверительного интервала при распределении отличном от нормального
В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.
Формула
Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы
где X – математическое ожидание выборки, α – уровень статистической значимости, tα – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.
Сам доверительный интервал может быть записан в следующем виде
Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.
Пример
Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.
В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят
А сам интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].
Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.
Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.
В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].
Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.
Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].
Выборки большого объема
К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.
Подведем итоги
В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.
Доверительный интервал
Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Содержание
Определение

Граничные точки доверительного интервала 

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ. [ссылка 2]
Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.
Примеры
Байесовский доверительный интервал
В байесовской статистике существует схожее, но отличающееся в некоторых ключевых деталях определение доверительного интервала. Здесь оцениваемый параметр 






Как правило, классический и байесовский доверительные интервалы различаются. В англоязычной литературе байесовский доверительный интервал принято называть термином credible interval, а классический — confidence interval.
Примечания
Полезное
Смотреть что такое «Доверительный интервал» в других словарях:
Доверительный интервал — интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов … Словарь-справочник терминов нормативно-технической документации
доверительный интервал — для скалярного параметра генеральной совокупности – это отрезок, с большой вероятностью содержащий этот параметр. Эта фраза без дальнейших уточнений бессмысленна. Поскольку границы доверительного интервала оцениваются по выборке, естественна его… … Словарь социологической статистики
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — (confidence interval) Интервал, в котором достоверность значения параметра по населению, полученного на основе выборочного обследования, имеет определенную степень вероятности, например 95%, что обусловлено самой выборкой (sample). Ширина… … Экономический словарь
доверительный интервал — – интервал, в котором находится истинное значение определяемой величины с заданной доверительной вероятностью. Общая химия : учебник / А. В. Жолнин [1] … Химические термины
Доверительный интервал ДИ — Доверительный интервал, ДИ * давяральны інтэрвал, ДІ * confidence interval интервал значения признака, рассчитанный для к. л. параметра распределения (напр., среднего значения признака) по выборке и с определенной вероятностью (напр., 95% для 95% … Генетика. Энциклопедический словарь
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — понятие, возникающее при оценке параметра статистич. распределения интервалом значений. Д. и. для параметра q, соответствующий данному коэф. доверия Р, равен такому интервалу (q1, q2), что при любом распределении вероятности неравенства… … Физическая энциклопедия
доверительный интервал — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN confidence interval … Справочник технического переводчика
доверительный интервал — pasikliovimo intervalas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultato vertė. atitikmenys: angl. confidence interval vok. Vertrauensbereich, m rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
доверительный интервал — pasikliovimo intervalas statusas T sritis chemija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultatų vertė. atitikmenys: angl. confidence interval rus. доверительная область; доверительный интервал … Chemijos terminų aiškinamasis žodynas
Доверительный интервал
Опубликовано 15.06.2021 · Обновлено 16.06.2021
Что такое Доверительный интервал?
Ключевые моменты
Понимание доверительного интервала
Статистики используют доверительные интервалы для измерения неопределенности переменной выборки. Например, исследователь случайным образом выбирает разные образцы из одной и той же совокупности и вычисляет доверительный интервал для каждой выборки, чтобы увидеть, как она может представлять истинное значение переменной совокупности. Все полученные наборы данных разные; некоторые интервалы включают параметр истинной популяции, а другие нет.
Краткая справка
Доверительный интервал и доверительный уровень взаимосвязаны, но не одно и то же.
Расчет доверительного интервала
Предположим, группа исследователей изучает рост баскетболистов средней школы. Исследователи выбирают случайную выборку из населения и устанавливают средний рост в 74 дюйма.
Среднее значение в 74 дюйма – это точечная оценка среднего значения для населения. Точечная оценка сама по себе имеет ограниченную полезность, потому что она не выявляет неопределенности, связанной с оценкой; у вас нет четкого представления о том, насколько далеко это среднее значение выборки в 74 дюйма может быть от среднего значения генеральной совокупности. Чего не хватает, так это степени неопределенности в этом единственном образце.
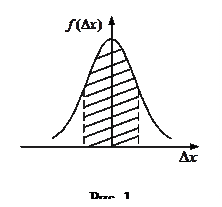
Доверительные интервалы предоставляют больше информации, чем точечные оценки. Установив 95% доверительный интервал с использованием среднего и стандартного отклонения по выборке и предположив нормальное распределение, представленное колоколообразной кривой, исследователи пришли к верхней и нижней границе, которая содержит истинное среднее значение в 95% случаев.
Предположим, что интервал составляет от 72 до 76 дюймов. Если исследователи возьмут 100 случайных выборок из популяции баскетболистов средней школы в целом, среднее значение должно быть от 72 до 76 дюймов в 95 из этих выборок.
Примеры доверительного интервала
Если исследователи хотят еще большей уверенности, они могут расширить интервал до 99% уверенности. Это неизменно приводит к более широкому диапазону, поскольку освобождает место для большего числа выборочных средних. Если они установят 99% доверительный интервал как от 70 до 78 дюймов, они могут ожидать, что 99 из 100 оцененных образцов будут содержать среднее значение между этими числами.
С другой стороны, уровень достоверности 90% означает, что мы ожидаем, что 90% интервальных оценок будут включать параметр генеральной совокупности и т. Д.
Особые соображения
Самое большое заблуждение относительно доверительных интервалов заключается в том, что они представляют собой процент данных из данной выборки, который попадает между верхней и нижней границами.
Доверительные интервалы
Сводные характеристики выборки для партии материала.
Для исследователя важно знать точность и надежность оценки каждого определенного параметра, представления о которых дают доверительные интервалы.
Односторонним доверительным интервалом называют интервал от Х- ε до неизвестного параметра или от неизвестного параметра до Х+ ε, который устанавливает либо нижнюю, либо верхнюю границу неизвестного параметра с заданной доверительной вероятностью Рд.
Двусторонним доверительным интервалом называют интервал от Х- ε до Х+ε, который покрывает неизвестный параметр распределения с заданной доверительной вероятностью Рд.
Доверительная ошибка ε характеризует случайную ошибку параметра распределения. Чем меньше значение ε тем больше точность оценки Х.
Доверительной вероятностью Рд или надежностью, соответствующей данному доверительному интервалу, называется вероятность того, что истинное значение многих числовых характеристик Х лежит в этом интервале.
Для контроля качества продукции доверительную вероятность Рд принимают равной 0,95 – 0,99.
Доверительный интервал ограничен нижней и верхней доверительными границами, в его пределах с некоторой вероятностью находится сводная характеристика.
Доверительные интервалы для среднего значения.
Для односторонней границы:
Нижняя граница: 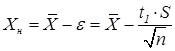
Верхняя граница: 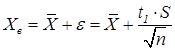
Для двусторонних границ:
Нижняя граница: 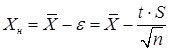
Верхняя граница: 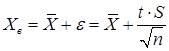
| K=n-1 | t1 | t | zн | zв | K =n-1 | t1 | t | zн | zв |
| 2,920 | 4,303 | 0,578 | 4,42 | 1,699 | 2,045 | 0,825 | 1,28 | ||
| 2,353 | 3,182 | 0,620 | 2,92 | 1,684 | 2,021 | 0,847 | 1,23 | ||
| 2,132 | 2,776 | 0,649 | 2,37 | 1,676 | 2,009 | 0,861 | 1,20 | ||
| 1,833 | 2,262 | 0,729 | 1,65 | 1,660 | 1,984 | 0,897 | 1,13 | ||
| 1,729 | 2,093 | 0,794 | 1,37 | ¥ | 1,645 | 1,960 | 1,000 | 1,00 |
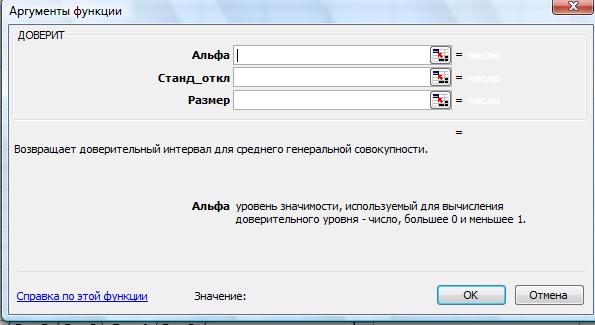
В программе Excel доверительные интервалы рассчитываются с помощью функции ДОВЕРИТ (рис. 22). Она возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности. Доверительный интервал представляет собой диапазон значений. Выборочное среднее x является серединой этого диапазона, следовательно, доверительный интервал определяется как (x ± ДОВЕРИТ).
Рис. 22. Функция ДОВЕРИТ
ДОВЕРИТ(альфа; станд_откл; размер)
Станд_откл — это стандартное отклонение (среднее квадратическое отклонение) генеральной совокупности для интервала данных, оно предполагается известным.
Размер — это размер выборки.
Если какой-либо из аргументов не является числом, то функция ДОВЕРИТ возвращает значение ошибки #ЗНАЧ!.
Если альфа ≤ 0 или альфа ≥ 1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!
Если станд_откл ≤ 0, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.
Если размер не целое, то оно округляется.
Если размер 100 значения Zн и Zв вычисляют по формулам:
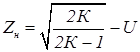
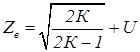
где U = t1 при n=∞ – квантиль распределения Стьюдента при доверительной вероятности Рд=0,95.
Доверительные интервалы для коэффициента вариации.
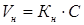
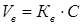
где С – коэффициент вариации.
Значения Кн и Кв приведены в таблице 6.
| n | ||||||
| Kн | 0,83 | 0,86 | 0,90 | 0,92 | 0,95 | 0,97 |
| Kв | 1,27 | 1,20 | 1,13 | 1,10 | 1,06 | 1,04 |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Доверительный интервал и доверительная вероятность



Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

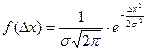
где 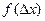


Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 
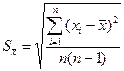
где 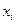
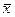
Чем больше число измерений, тем меньше 
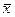

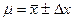
Интервал значений от 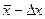
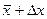

Все это справедливо для достаточно большого числа измерений, когда 
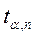


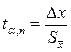
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α
Таблица 1.
| n | α | n | α | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 |
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 |
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 |
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 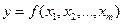
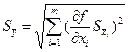
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.