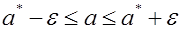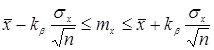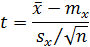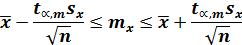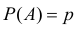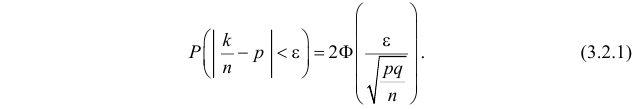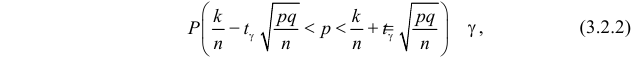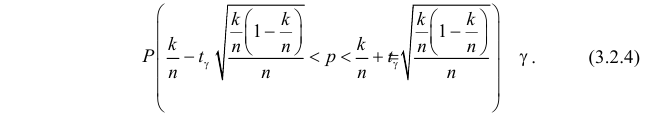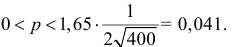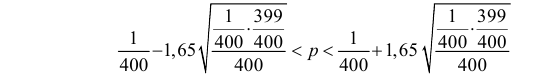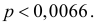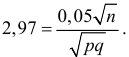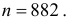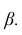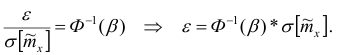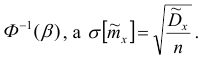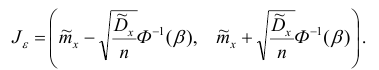Что называют доверительным интервалом и как он измеряется при увеличении надежности
Доверительные интервалы
Определение
Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.
Нормальное распределение
Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.
Формула
Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула
где X – математическое ожидание выборки, α – уровень статистической значимости, Zα/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.
Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде
Пример
Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Zα/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят
А сам доверительный интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.
Методы сужения доверительного интервала
Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.
Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Zα/2=1,64. В этом случае нижняя и верхняя граница интервала составят
А сам доверительный интервал может быть записан в виде
В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].
Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов
Сам доверительный интервал станет иметь следующий вид
Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.
Построение доверительного интервала при распределении отличном от нормального
В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.
Формула
Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы
где X – математическое ожидание выборки, α – уровень статистической значимости, tα – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.
Сам доверительный интервал может быть записан в следующем виде
Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.
Пример
Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.
В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят
А сам интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].
Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.
Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.
В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].
Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.
Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].
Выборки большого объема
К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.
Подведем итоги
В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.
Доверительные интервалы и доверительная вероятность
Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.
В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.
Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Пусть для генерального параметра a получена из опыта несмещенная оценка a*. Нужно оценить возможную при этом ошибку. Назначим достаточно большую вероятность β – такую, что событие с этой вероятностью можно считать практически достоверным, и найдем такое значение ε для которого

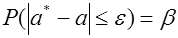
называемой уровнем значимости или риском. Уровень значимости часто выражают в процентах. Иначе формулу ( (5.8.1* ) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах
Вероятность β называется доверительной вероятностью, доверительным уровнем или надежностью, т.к. она характеризует надежность полученной оценки.
Интервал 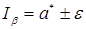
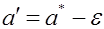
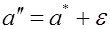
При этом отметим следующее. Ранее мы рассматривали вероятность попадания случайной величины на заданный (неслучайный) интервал. В данном случае дело обстоит иначе: величина ане случайна, зато случаен интервал I b . Случайно его положение на числовой прямой, определяемое его центром а * , случайна и длина интервала 2 e, так как величина e вычисляется, как правило, по опытным данным, т.е. по результатам эксперимента. Поэтому в рассматриваемом случае удобно толковать интервал I как вероятность того, что случайный интервал I b накроет величину а.
Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра внутри доверительного интервала: чем больше величина β, тем больше и ε (т.е. с чем большей вероятностью мы хотим гарантировать полученный результат, тем в большем интервале он должен находиться).
Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
ППри построении доверительного интервала решается задача об абсолютном отклонении:
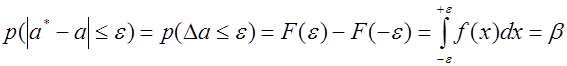
Таким образом, если известен закон распределения оценки a*, то задача определения доверительного интервала решается довольно просто.
Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины с известным генеральным стандартом σх.
Понятие генерального стандарта тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям
Пусть имеется выборка объема n значений случайной величины. Оценкой mx является среднее выборки:
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально можно показать, что 
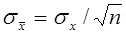
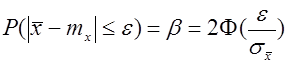
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 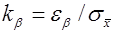
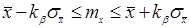
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1) приближенный – при n более 50 заменяют неизвестные параметры их оценками;
2) от случайной величины a * переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра а, а зависит только от объема выборки n и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
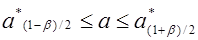
Если выразить через р,
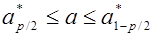
На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 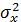
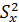
t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала
Дата добавления: 2020-12-22 ; просмотров: 513 ; Мы поможем в написании вашей работы!
Доверительный интервал
Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Содержание
Определение

Граничные точки доверительного интервала 

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ. [ссылка 2]
Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.
Примеры
Байесовский доверительный интервал
В байесовской статистике существует схожее, но отличающееся в некоторых ключевых деталях определение доверительного интервала. Здесь оцениваемый параметр 






Как правило, классический и байесовский доверительные интервалы различаются. В англоязычной литературе байесовский доверительный интервал принято называть термином credible interval, а классический — confidence interval.
Примечания
Полезное
Смотреть что такое «Доверительный интервал» в других словарях:
Доверительный интервал — интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов … Словарь-справочник терминов нормативно-технической документации
доверительный интервал — для скалярного параметра генеральной совокупности – это отрезок, с большой вероятностью содержащий этот параметр. Эта фраза без дальнейших уточнений бессмысленна. Поскольку границы доверительного интервала оцениваются по выборке, естественна его… … Словарь социологической статистики
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — (confidence interval) Интервал, в котором достоверность значения параметра по населению, полученного на основе выборочного обследования, имеет определенную степень вероятности, например 95%, что обусловлено самой выборкой (sample). Ширина… … Экономический словарь
доверительный интервал — – интервал, в котором находится истинное значение определяемой величины с заданной доверительной вероятностью. Общая химия : учебник / А. В. Жолнин [1] … Химические термины
Доверительный интервал ДИ — Доверительный интервал, ДИ * давяральны інтэрвал, ДІ * confidence interval интервал значения признака, рассчитанный для к. л. параметра распределения (напр., среднего значения признака) по выборке и с определенной вероятностью (напр., 95% для 95% … Генетика. Энциклопедический словарь
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — понятие, возникающее при оценке параметра статистич. распределения интервалом значений. Д. и. для параметра q, соответствующий данному коэф. доверия Р, равен такому интервалу (q1, q2), что при любом распределении вероятности неравенства… … Физическая энциклопедия
доверительный интервал — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN confidence interval … Справочник технического переводчика
доверительный интервал — pasikliovimo intervalas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultato vertė. atitikmenys: angl. confidence interval vok. Vertrauensbereich, m rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
доверительный интервал — pasikliovimo intervalas statusas T sritis chemija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultatų vertė. atitikmenys: angl. confidence interval rus. доверительная область; доверительный интервал … Chemijos terminų aiškinamasis žodynas
Доверительный интервал для вероятности события:
Пусть вероятность
По заданному уровню надежности 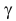
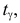
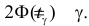
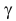
откуда 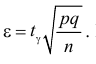
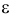
К сожалению, в формуле (3.2.2) доверительные границы для вероятности 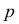
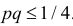
Оценка 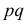
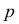
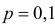
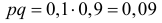
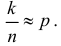
Пример:
Для обследования большой партии изделий (несколько тысяч штук) наугад выбрано 160 изделий. Среди них оказалось 56 изделий низкого сорта. Оценить долю изделий низкого сорта в этой партии с надежностью 0,95.
Решение. Так как партия изделий крупная, то для упрощения можно считать, что по мере выбора изделий состав партии заметно не изменяется и вероятность выбрать наугад изделие низкого сорта равна доле низкосортных изделий в этой партии. Тогда задача сводится к построению доверительного интервала для вероятности выбрать из этой партии изделие низкого сорта. Частота изделий низкого сорта в выборке равна 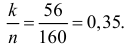
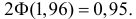
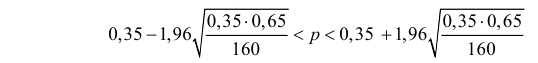
или 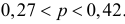
Пример:
Было проведено 400 испытаний механизма катапультирования. В этих испытания не зарегистрировано ни одного отказа. С надежностью 0,95 оценить вероятность отказа механизма катапультирования.
Решение. В данной серии испытаний частота появления отказа 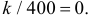
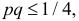
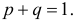
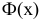
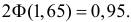
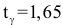
Еще раз подчеркнем, что доверительный интервал (3.2.3) построен в расчете на худший вариант, когда вероятность события близка к 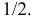
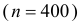
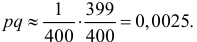
или 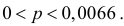
Ответ.
Пример:
При штамповке 70% деталей выходит первым сортом, 20% – вторым и 10% – третьим. Определить, сколько нужно взять деталей, чтобы с вероятностью равной 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортной детали не более чем на 0,05 в ту или другую сторону? Ответить на тот же вопрос, если процент первосортных деталей неизвестен.
Решение. Изготовление каждой детали можно считать независимым испытанием с вероятностью «успеха» 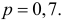
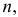
По таблице функции Лапласа (см. прил., табл. П2) находим, что 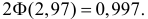
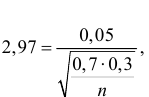
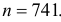
Учитывая, что 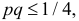
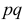
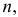
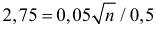
Доверительные вероятности, доверительные интервалы
В материалах сегодняшней лекции мы рассмотрим доверительные вероятности и доверительные интервалы.
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 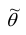
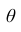
Доверительным интервалом для параметра 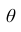
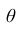
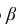
Число 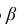
Пусть 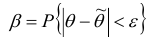
0,95. ).
Так как 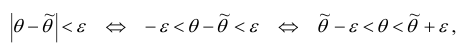
интервал 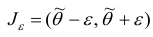
Интервал 
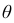
Покажем, как найти доверительный интервал для математического ожидания 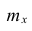
Пусть 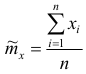
Используя центральную предельную теорему, можно считать, что случайная величина 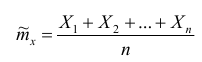
Тогда 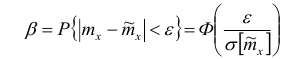
Отсюда
Здесь 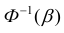
значению 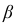
Таким образом, доверительный интервал для математического ожидании имеет вид
Заключение по лекции:
В лекции мы рассмотрели доверительные вероятности и доверительные интервалы.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.