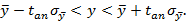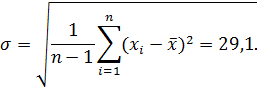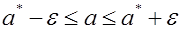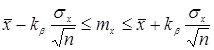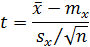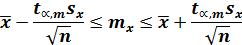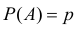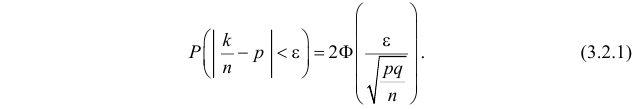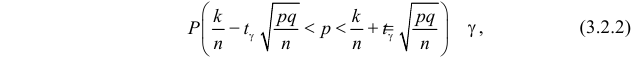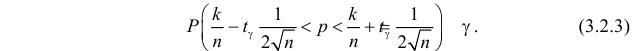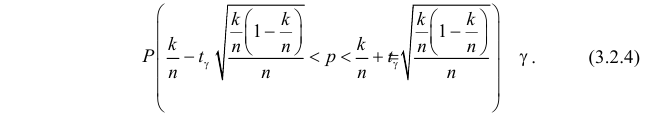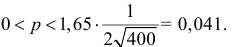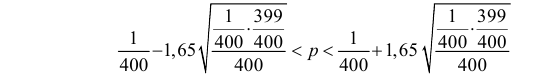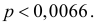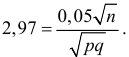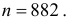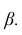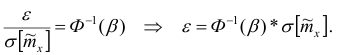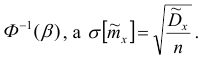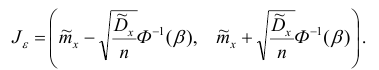Что называют доверительным интервалом и доверительной вероятностью надежностью
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
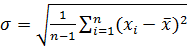
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 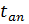
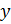
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 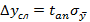
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Доверительные интервалы и доверительная вероятность
Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.
В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.
Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Пусть для генерального параметра a получена из опыта несмещенная оценка a*. Нужно оценить возможную при этом ошибку. Назначим достаточно большую вероятность β – такую, что событие с этой вероятностью можно считать практически достоверным, и найдем такое значение ε для которого

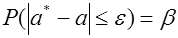
называемой уровнем значимости или риском. Уровень значимости часто выражают в процентах. Иначе формулу ( (5.8.1* ) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах
Вероятность β называется доверительной вероятностью, доверительным уровнем или надежностью, т.к. она характеризует надежность полученной оценки.
Интервал 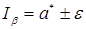
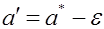
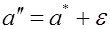
При этом отметим следующее. Ранее мы рассматривали вероятность попадания случайной величины на заданный (неслучайный) интервал. В данном случае дело обстоит иначе: величина ане случайна, зато случаен интервал I b . Случайно его положение на числовой прямой, определяемое его центром а * , случайна и длина интервала 2 e, так как величина e вычисляется, как правило, по опытным данным, т.е. по результатам эксперимента. Поэтому в рассматриваемом случае удобно толковать интервал I как вероятность того, что случайный интервал I b накроет величину а.
Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра внутри доверительного интервала: чем больше величина β, тем больше и ε (т.е. с чем большей вероятностью мы хотим гарантировать полученный результат, тем в большем интервале он должен находиться).
Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
ППри построении доверительного интервала решается задача об абсолютном отклонении:
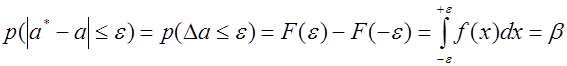
Таким образом, если известен закон распределения оценки a*, то задача определения доверительного интервала решается довольно просто.
Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины с известным генеральным стандартом σх.
Понятие генерального стандарта тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям
Пусть имеется выборка объема n значений случайной величины. Оценкой mx является среднее выборки:
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально можно показать, что 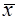
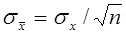
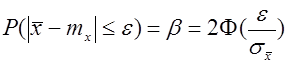
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 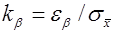
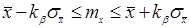
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1) приближенный – при n более 50 заменяют неизвестные параметры их оценками;
2) от случайной величины a * переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра а, а зависит только от объема выборки n и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
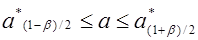
Если выразить через р,
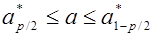
На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 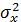
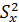
t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала
Дата добавления: 2020-12-22 ; просмотров: 512 ; Мы поможем в написании вашей работы!
Точность оценки, доверительная вероятность (надежность). Доверительный интервал
Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше,- точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Однако важно подчеркнуть, что для малых выборок (n 2 с k степенями свободы, то величина

распределена по закону Стьюдента с k степенями свободы. Пусть количественный признак X генеральной совокупности распределен нормально, причем М(Х)=а, σ(Х)= σ. Если из этой совокупности извлекать выборки объема n и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. VIII, § 9)


Тогда случайная величина

также имеет нормальное распределение как линейная функция нормального аргумента 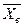

Следовательно, подставив (**) и (***) в (*), получим величину

которая распределена по закону Стьюдента с k = n-1 степенями свободы.
Доверительный интервал и доверительная вероятность



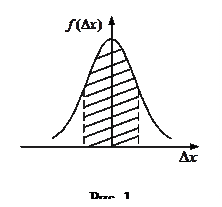
Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

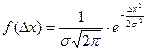
где 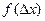


Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 
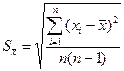
где 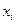
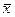
Чем больше число измерений, тем меньше 
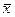

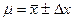
Интервал значений от 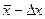
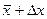

Все это справедливо для достаточно большого числа измерений, когда 
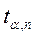


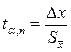
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α
Таблица 1.
| n | α | n | α | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 |
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 |
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 |
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 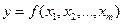
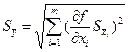
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Доверительный интервал для вероятности события:
Пусть вероятность
По заданному уровню надежности 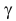
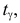
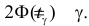
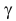
откуда 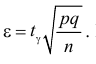
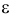
К сожалению, в формуле (3.2.2) доверительные границы для вероятности 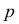
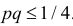
Оценка 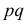
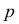
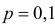
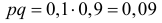
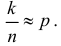
Пример:
Для обследования большой партии изделий (несколько тысяч штук) наугад выбрано 160 изделий. Среди них оказалось 56 изделий низкого сорта. Оценить долю изделий низкого сорта в этой партии с надежностью 0,95.
Решение. Так как партия изделий крупная, то для упрощения можно считать, что по мере выбора изделий состав партии заметно не изменяется и вероятность выбрать наугад изделие низкого сорта равна доле низкосортных изделий в этой партии. Тогда задача сводится к построению доверительного интервала для вероятности выбрать из этой партии изделие низкого сорта. Частота изделий низкого сорта в выборке равна 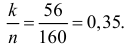
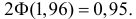
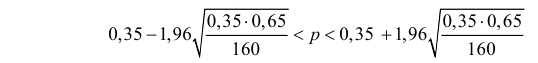
или 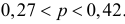
Пример:
Было проведено 400 испытаний механизма катапультирования. В этих испытания не зарегистрировано ни одного отказа. С надежностью 0,95 оценить вероятность отказа механизма катапультирования.
Решение. В данной серии испытаний частота появления отказа 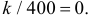
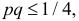
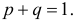
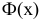
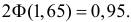
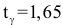
Еще раз подчеркнем, что доверительный интервал (3.2.3) построен в расчете на худший вариант, когда вероятность события близка к 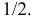
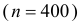
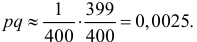
или 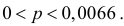
Ответ.
Пример:
При штамповке 70% деталей выходит первым сортом, 20% – вторым и 10% – третьим. Определить, сколько нужно взять деталей, чтобы с вероятностью равной 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортной детали не более чем на 0,05 в ту или другую сторону? Ответить на тот же вопрос, если процент первосортных деталей неизвестен.
Решение. Изготовление каждой детали можно считать независимым испытанием с вероятностью «успеха» 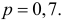
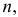
По таблице функции Лапласа (см. прил., табл. П2) находим, что 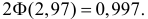
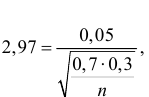
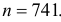
Учитывая, что 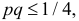
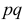
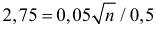
Доверительные вероятности, доверительные интервалы
В материалах сегодняшней лекции мы рассмотрим доверительные вероятности и доверительные интервалы.
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 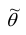
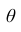
Доверительным интервалом для параметра 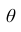
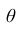
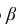
Число 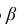
Пусть 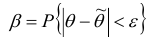
0,95. ).
Так как 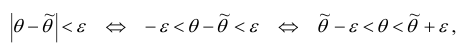
интервал 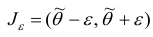
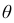
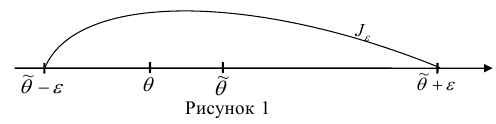
Интервал 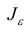
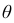
Покажем, как найти доверительный интервал для математического ожидания 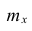
Пусть 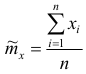
Используя центральную предельную теорему, можно считать, что случайная величина 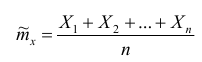
Тогда 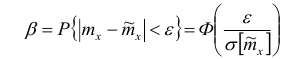
Отсюда
Здесь 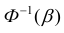
значению 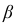
Таким образом, доверительный интервал для математического ожидании имеет вид
Заключение по лекции:
В лекции мы рассмотрели доверительные вероятности и доверительные интервалы.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.