Что называют данными в машинном обучении матрицы объекты признаки алгоритм функция
Как говорить о данных в машинном обучении (терминология из статистики и информатики)
Дата публикации 2016-03-09
Данные играют большую роль в машинном обучении.
При понимании данных важно понимать и использовать правильную терминологию.
В этом посте вы узнаете, как именно описать и рассказать о данных в машинном обучении. Прочитав этот пост, вы узнаете терминологию и номенклатуру, используемые в машинном обучении для описания данных.
Это очень поможет вам в понимании алгоритмов машинного обучения в целом.
Данные, как вы это знаете
Как вы относитесь к данным?
Подумайте о таблице, как Microsoft Excel. У вас есть столбцы, строки и ячейки.
Вот как вы, вероятно, думаете о данных, столбцах, строках и ячейках.
Как правило, мы можем назвать этот тип данных: табличные данные. Эта форма данных легко работать в рамках машинного обучения.
Данные, как они известны в машинном обучении
Существуют разные виды машинного обучения, которые дают разные взгляды на поле. Например, есть статистическая перспектива и перспектива информатики.
Далее мы рассмотрим различные термины, используемые для обозначения данных, какими вы их знаете.
Статистическая перспектива обучения
Статистическая перспектива формирует данные в контексте гипотетической функции (f), которую пытается изучить алгоритм машинного обучения.
То есть, учитывая некоторые входные переменные (входные), какова прогнозируемая выходная переменная (выходные данные).
Те столбцы, которые являются входными данными, называются входными переменными.
Принимая во внимание, что столбец данных, который вы не всегда можете иметь и который вы хотели бы прогнозировать для новых входных данных в будущем, называется выходной переменной. Это также называется переменной ответа.
выходная переменная = f (входные переменные)
Как правило, у вас есть более одной входной переменной. В этом случае группа входных переменных называется входным вектором.
выходная переменная = f (входной вектор)
Если вы делали небольшую статистику в прошлом, вы можете знать другую, более традиционную терминологию.
Например, текст статистики может говорить о входных переменных как независимых переменных и выходной переменной как зависимой переменной. Это связано с тем, что при формулировании задачи прогнозирования выходные данные являются зависимыми или являются функцией входных данных или независимых переменных.
зависимая переменная = f (независимые переменные)
Когда у вас есть несколько входных переменных, они могут быть разыменованы с целым числом, чтобы указать их порядок во входном векторе, например, X1, X2 и X3 для данных в первых трех столбцах.
Перспектива информатики
Существует много совпадений в терминологии информатики для данных со статистической точки зрения. Мы рассмотрим ключевые отличия.
Строка часто описывает сущность (например, человека) или наблюдение за сущностью. Таким образом, столбцы для строки часто упоминаются как атрибуты наблюдения. При моделировании проблемы и прогнозировании мы можем ссылаться на входные и выходные атрибуты.
выходной атрибут = программа (входные атрибуты)
Примеры этого включают аналоговые данные, такие как изображения, аудио и видео.
выход = программа (входные функции)
прогноз = программа (экземпляр)
Модели и алгоритмы
Есть одно заключительное замечание прояснения, которое важно и это между алгоритмами и моделями.
Это может сбивать с толку, так как алгоритм и модель могут использоваться взаимозаменяемо
модель = алгоритм (данные)
Резюме
В этом посте вы обнаружили ключевую терминологию, используемую для описания данных в машинном обучении.
Есть ли у вас какие-либо вопросы об этом посте или о терминологии данных, используемой в машинном обучении? Оставьте комментарий и задайте свой вопрос, и я сделаю все возможное, чтобы ответить на него.
Введение в машинное обучение
1.1 Введение
Благодаря машинному обучению программист не обязан писать инструкции, учитывающие все возможные проблемы и содержащие все решения. Вместо этого в компьютер (или отдельную программу) закладывают алгоритм самостоятельного нахождения решений путём комплексного использования статистических данных, из которых выводятся закономерности и на основе которых делаются прогнозы.
Технология машинного обучения на основе анализа данных берёт начало в 1950 году, когда начали разрабатывать первые программы для игры в шашки. За прошедшие десятилетий общий принцип не изменился. Зато благодаря взрывному росту вычислительных мощностей компьютеров многократно усложнились закономерности и прогнозы, создаваемые ими, и расширился круг проблем и задач, решаемых с использованием машинного обучения.
Чтобы запустить процесс машинного обучение, для начала необходимо загрузить в компьютер Датасет(некоторое количество исходных данных), на которых алгоритм будет учиться обрабатывать запросы. Например, могут быть фотографии собак и котов, на которых уже есть метки, обозначающие к кому они относятся. После процесса обучения, программа уже сама сможет распознавать собак и котов на новых изображениях без содержания меток. Процесс обучения продолжается и после выданных прогнозов, чем больше данных мы проанализировали программой, тем более точно она распознает нужные изображения.
Благодаря машинному обучению компьютеры учатся распознавать на фотографиях и рисунках не только лица, но и пейзажи, предметы, текст и цифры. Что касается текста, то и здесь не обойтись без машинного обучения: функция проверки грамматики сейчас присутствует в любом текстовом редакторе и даже в телефонах. Причем учитывается не только написание слов, но и контекст, оттенки смысла и другие тонкие лингвистические аспекты. Более того, уже существует программное обеспечение, способное без участия человека писать новостные статьи (на тему экономики и, к примеру, спорта).
1.2 Типы задач машинного обучения
Все задачи, решаемые с помощью ML, относятся к одной из следующих категорий.
1)Задача регрессии – прогноз на основе выборки объектов с различными признаками. На выходе должно получиться вещественное число (2, 35, 76.454 и др.), к примеру цена квартиры, стоимость ценной бумаги по прошествии полугода, ожидаемый доход магазина на следующий месяц, качество вина при слепом тестировании.
2)Задача классификации – получение категориального ответа на основе набора признаков. Имеет конечное количество ответов (как правило, в формате «да» или «нет»): есть ли на фотографии кот, является ли изображение человеческим лицом, болен ли пациент раком.
3)Задача кластеризации – распределение данных на группы: разделение всех клиентов мобильного оператора по уровню платёжеспособности, отнесение космических объектов к той или иной категории (планета, звёзда, чёрная дыра и т. п.).
4)Задача уменьшения размерности – сведение большого числа признаков к меньшему (обычно 2–3) для удобства их последующей визуализации (например, сжатие данных).
5)Задача выявления аномалий – отделение аномалий от стандартных случаев. На первый взгляд она совпадает с задачей классификации, но есть одно существенное отличие: аномалии – явление редкое, и обучающих примеров, на которых можно натаскать машинно обучающуюся модель на выявление таких объектов, либо исчезающе мало, либо просто нет, поэтому методы классификации здесь не работают. На практике такой задачей является, например, выявление мошеннических действий с банковскими картами.
1.3 Основные виды машинного обучения
Основная масса задач, решаемых при помощи методов машинного обучения, относится к двум разным видам: обучение с учителем (supervised learning) либо без него (unsupervised learning). Однако этим учителем вовсе не обязательно является сам программист, который стоит над компьютером и контролирует каждое действие в программе. «Учитель» в терминах машинного обучения – это само вмешательство человека в процесс обработки информации. В обоих видах обучения машине предоставляются исходные данные, которые ей предстоит проанализировать и найти закономерности. Различие лишь в том, что при обучении с учителем есть ряд гипотез, которые необходимо опровергнуть или подтвердить. Эту разницу легко понять на примерах.
Машинное обучение с учителем
Предположим, в нашем распоряжении оказались сведения о десяти тысячах московских квартир: площадь, этаж, район, наличие или отсутствие парковки у дома, расстояние от метро, цена квартиры и т. п. Нам необходимо создать модель, предсказывающую рыночную стоимость квартиры по её параметрам. Это идеальный пример машинного обучения с учителем: у нас есть исходные данные (количество квартир и их свойства, которые называются признаками) и готовый ответ по каждой из квартир – её стоимость. Программе предстоит решить задачу регрессии.
Ещё пример из практики: подтвердить или опровергнуть наличие рака у пациента, зная все его медицинские показатели. Выяснить, является ли входящее письмо спамом, проанализировав его текст. Это всё задачи на классификацию.
Машинное обучение без учителя
В случае обучения без учителя, когда готовых «правильных ответов» системе не предоставлено, всё обстоит ещё интереснее. Например, у нас есть информация о весе и росте какого-то количества людей, и эти данные нужно распределить по трём группам, для каждой из которых предстоит пошить рубашки подходящих размеров. Это задача кластеризации. В этом случае предстоит разделить все данные на 3 кластера (но, как правило, такого строгого и единственно возможного деления нет).
Если взять другую ситуацию, когда каждый из объектов в выборке обладает сотней различных признаков, то основной трудностью будет графическое отображение такой выборки. Поэтому количество признаков уменьшают до двух или трёх, и становится возможным визуализировать их на плоскости или в 3D. Это – задача уменьшения размерности.
1.4 Основные алгоритмы моделей машинного обучения
1. Дерево принятия решений
Это метод поддержки принятия решений, основанный на использовании древовидного графа: модели принятия решений, которая учитывает их потенциальные последствия (с расчётом вероятности наступления того или иного события), эффективность, ресурсозатратность.
Для бизнес-процессов это дерево складывается из минимального числа вопросов, предполагающих однозначный ответ — «да» или «нет». Последовательно дав ответы на все эти вопросы, мы приходим к правильному выбору. Методологические преимущества дерева принятия решений – в том, что оно структурирует и систематизирует проблему, а итоговое решение принимается на основе логических выводов.
2. Наивная байесовская классификация
Наивные байесовские классификаторы относятся к семейству простых вероятностных классификаторов и берут начало из теоремы Байеса, которая применительно к данному случаю рассматривает функции как независимые (это называется строгим, или наивным, предположением). На практике используется в следующих областях машинного обучения:
Всем, кто хоть немного изучал статистику, знакомо понятие линейной регрессии. К вариантам её реализации относятся и наименьшие квадраты. Обычно с помощью линейной регрессии решают задачи по подгонке прямой, которая проходит через множество точек. Вот как это делается с помощью метода наименьших квадратов: провести прямую, измерить расстояние от неё до каждой из точек (точки и линию соединяют вертикальными отрезками), получившуюся сумму перенести наверх. В результате та кривая, в которой сумма расстояний будет наименьшей, и есть искомая (эта линия пройдёт через точки с нормально распределённым отклонением от истинного значения).
Линейная функция обычно используется при подборе данных для машинного обучения, а метод наименьших квадратов – для сведения к минимуму погрешностей путем создания метрики ошибок.
4. Логистическая регрессия
Логистическая регрессия – это способ определения зависимости между переменными, одна из которых категориально зависима, а другие независимы. Для этого применяется логистическая функция (аккумулятивное логистическое распределение). Практическое значение логистической регрессии заключается в том, что она является мощным статистическим методом предсказания событий, который включает в себя одну или несколько независимых переменных. Это востребовано в следующих ситуациях:
Это целый набор алгоритмов, необходимых для решения задач на классификацию и регрессионный анализ. Исходя из того что объект, находящийся в N-мерном пространстве, относится к одному из двух классов, метод опорных векторов строит гиперплоскость с мерностью (N – 1), чтобы все объекты оказались в одной из двух групп. На бумаге это можно изобразить так: есть точки двух разных видов, и их можно линейно разделить. Кроме сепарации точек, данный метод генерирует гиперплоскость таким образом, чтобы она была максимально удалена от самой близкой точки каждой группы.
SVM и его модификации помогают решать такие сложные задачи машинного обучения, как сплайсинг ДНК, определение пола человека по фотографии, вывод рекламных баннеров на сайты.
Он базируется на алгоритмах машинного обучения, генерирующих множество классификаторов и разделяющих все объекты из вновь поступающих данных на основе их усреднения или итогов голосования. Изначально метод ансамблей был частным случаем байесовского усреднения, но затем усложнился и оброс дополнительными алгоритмами:
Кластеризация заключается в распределении множества объектов по категориям так, чтобы в каждой категории – кластере – оказались наиболее схожие между собой элементы.
Кластеризировать объекты можно по разным алгоритмам. Чаще всего используют следующие:
8. Метод главных компонент (PCA)
Метод главных компонент, или PCA, представляет собой статистическую операцию по ортогональному преобразованию, которая имеет своей целью перевод наблюдений за переменными, которые могут быть как-то взаимосвязаны между собой, в набор главных компонент – значений, которые линейно не коррелированы.
Практические задачи, в которых применяется PCA, – визуализация и большинство процедур сжатия, упрощения, минимизации данных для того, чтобы облегчить процесс обучения. Однако метод главных компонент не годится для ситуаций, когда исходные данные слабо упорядочены (то есть все компоненты метода характеризуются высокой дисперсией). Так что его применимость определяется тем, насколько хорошо изучена и описана предметная область.
9. Сингулярное разложение
В линейной алгебре сингулярное разложение, или SVD, определяется как разложение прямоугольной матрицы, состоящей из комплексных или вещественных чисел. Так, матрицу M размерностью [m*n] можно разложить таким образом, что M = UΣV, где U и V будут унитарными матрицами, а Σ – диагональной.
Одним из частных случаев сингулярного разложения является метод главных компонент. Самые первые технологии компьютерного зрения разрабатывались на основе SVD и PCA и работали следующим образом: вначале лица (или другие паттерны, которые предстояло найти) представляли в виде суммы базисных компонент, затем уменьшали их размерность, после чего производили их сопоставление с изображениями из выборки. Современные алгоритмы сингулярного разложения в машинном обучении, конечно, значительно сложнее и изощрённее, чем их предшественники, но суть их в целом нем изменилась.
10. Анализ независимых компонент (ICA)
Это один из статистических методов, который выявляет скрытые факторы, оказывающие влияние на случайные величины, сигналы и пр. ICA формирует порождающую модель для баз многофакторных данных. Переменные в модели содержат некоторые скрытые переменные, причем нет никакой информации о правилах их смешивания. Эти скрытые переменные являются независимыми компонентами выборки и считаются негауссовскими сигналами.
В отличие от анализа главных компонент, который связан с данным методом, анализ независимых компонент более эффективен, особенно в тех случаях, когда классические подходы оказываются бессильны. Он обнаруживает скрытые причины явлений и благодаря этому нашёл широкое применение в самых различных областях – от астрономии и медицины до распознавания речи, автоматического тестирования и анализа динамики финансовых показателей.
1.5 Примеры применения в реальной жизни
Пример 1. Диагностика заболеваний
Пациенты в данном случае являются объектами, а признаками – все наблюдающиеся у них симптомы, анамнез, результаты анализов, уже предпринятые лечебные меры (фактически вся история болезни, формализованная и разбитая на отдельные критерии). Некоторые признаки – пол, наличие или отсутствие головной боли, кашля, сыпи и иные – рассматриваются как бинарные. Оценка тяжести состояния (крайне тяжёлое, средней тяжести и др.) является порядковым признаком, а многие другие – количественными: объём лекарственного препарата, уровень гемоглобина в крови, показатели артериального давления и пульса, возраст, вес. Собрав информацию о состоянии пациента, содержащую много таких признаков, можно загрузить её в компьютер и с помощью программы, способной к машинному обучению, решить следующие задачи:
Пример 2. Поиск мест залегания полезных ископаемых
В роли признаков здесь выступают сведения, добытые при помощи геологической разведки: наличие на территории местности каких-либо пород (и это будет признаком бинарного типа), их физические и химические свойства (которые раскладываются на ряд количественных и качественных признаков).
Для обучающей выборки берутся 2 вида прецедентов: районы, где точно присутствуют месторождения полезных ископаемых, и районы с похожими характеристиками, где эти ископаемые не были обнаружены. Но добыча редких полезных ископаемых имеет свою специфику: во многих случаях количество признаков значительно превышает число объектов, и методы традиционной статистики плохо подходят для таких ситуаций. Поэтому при машинном обучении акцент делается на обнаружение закономерностей в уже собранном массиве данных. Для этого определяются небольшие и наиболее информативные совокупности признаков, которые максимально показательны для ответа на вопрос исследования – есть в указанной местности то или иное ископаемое или нет. Можно провести аналогию с медициной: у месторождений тоже можно выявить свои синдромы. Ценность применения машинного обучения в этой области заключается в том, что полученные результаты не только носят практический характер, но и представляют серьёзный научный интерес для геологов и геофизиков.
Пример 3. Оценка надёжности и платёжеспособности кандидатов на получение кредитов
С этой задачей ежедневно сталкиваются все банки, занимающиеся выдачей кредитов. Необходимость в автоматизации этого процесса назрела давно, ещё в 1960–1970-е годы, когда в США и других странах начался бум кредитных карт.
Лица, запрашивающие у банка заём, – это объекты, а вот признаки будут отличаться в зависимости от того, физическое это лицо или юридическое. Признаковое описание частного лица, претендующего на кредит, формируется на основе данных анкеты, которую оно заполняет. Затем анкета дополняется некоторыми другими сведениями о потенциальном клиенте, которые банк получает по своим каналам. Часть из них относятся к бинарным признакам (пол, наличие телефонного номера), другие — к порядковым (образование, должность), большинство же являются количественными (величина займа, общая сумма задолженностей по другим банкам, возраст, количество членов семьи, доход, трудовой стаж) или номинальными (имя, название фирмы-работодателя, профессия, адрес).
Для машинного обучения составляется выборка, в которую входят кредитополучатели, чья кредитная история известна. Все заёмщики делятся на классы, в простейшем случае их 2 – «хорошие» заёмщики и «плохие», и положительное решение о выдаче кредита принимается только в пользу «хороших».
Более сложный алгоритм машинного обучения, называемый кредитным скорингом, предусматривает начисление каждому заёмщику условных баллов за каждый признак, и решение о предоставлении кредита будет зависеть от суммы набранных баллов. Во время машинного обучения системы кредитного скоринга вначале назначают некоторое количество баллов каждому признаку, а затем определяют условия выдачи займа (срок, процентную ставку и остальные параметры, которые отражаются в кредитном договоре). Но существует также и другой алгоритм обучения системы – на основе прецедентов.
Введение в машинное обучение
Полный курс на русском языке можно найти по этой ссылке.
Оригинальный курс на английском доступен по этой ссылке.
Выход новых лекций запланирован каждые 2-3 дня.
Интервью с Себастьяном Труном, CEO Udacity
— И снова всем привет, с вами я, Пейдж и сегодня со мной гость — Себастьян.
— Привет, я Себастьян!
— … человек у которого невероятная карьера, успевшего сделать множество потрясающих вещей! Вы являетесь со-основателем Udacity, вы основали Google X, вы професcор в Стэнфорде. Вы занимались невероятными исследованиями и глубоким обучением на всём протяжении своей карьеры. Что приносило вам наибольшее удовлетворение и в какой из областей вы получали наибольшее вознаграждение за проделанную работу?
— Скажу честно, я очень люблю находиться в Кремниевой долине! Мне нравится находится рядом с людьми, которые значительно умнее меня, и я всегда рассматривал технологии, как инструмент менющий правила игры различными способами — начиная от образования и заканчивая логистикой, здравохранением и т.д. Всё это меняется настолько быстро, и возникает невероятное желание быть участником этих изменений, наблюдать за ними. Ты смотришь на окружающее тебя и понимаешь, что большинство из того, что ты видишь вокруг, не работает так, как это должно — всегда можно изобрести нечто новое!
— Ну что ж, это очень оптимистичный взгляд на технологии! Какой момент на протяжении всей вашей карьеры был самой большой «эврикой»?
— Господи, их было так много! Помню один из дней, когда Ларри Пейдж позвонил мне и предложил создать автопилотируемые автомобили, которые смогли бы проезжать по всем улицам Калифорнии. В то время я считался экспертом, меня к таковым причисляли и, я был тем самым человеком, который сказал «нет, этого нельзя сделать». После этого Ларри убедил меня, что, в принципе, это возможно сделать, стоит только начать и сделать попытку. И мы сделали это! Это был момент, когда я осознал, что даже эксперты ошибаются и говоря «нет» мы на 100% становимся пессимистами. Я думаю мы должны быть более открыты новому.
— Или, например, если вам звонит Ларри Пейдж и говорит, — «Хэй, сделай крутую вещь вроде Google X» и получается нечто достаточно крутое!
— Да, это точно, жаловаться не приходится! Я имею ввиду, что всё это — процесс, который проходит через множество обсуждений на пути к реализации. Мне, действительно, повезло работать и я горжусь этим, в Google X и над другими проектами.
— Потрясающе! Итак, этот курс полностью о работе с TensorFlow. У вас есть опыт использования TensorFlow или может быть вы знакомы (слышали) с ним?
— Да! Я, в буквальном смысле, люблю TensorFlow, конечно! В моей собственной лаборатории мы используем его часто и много, одна из самых значимых работ на основе TensorFlow вышла около двух лет назад. Мы узнали, что iPhone и Android могут быть эффективнее в определении рака кожи, чем лучшие дерматологи в мире. Своё исследование мы опубликовали в Nature и это произвело своего рода переполох в медицине.
— Звучит потрясающе! Значит вы знаете и любите TensorFlow, что само по себе здорово! Вы уже успели поработать с TensorFlow 2.0?
— Нет, к сожалению пока не успел.
— Он будет просто восхитителен! Все студенты этого курса будут работать с этой версией.
— Я завидую им! Обязательно попробую!
— Прекрасно! На нашем курсе очень много студентов, которые в своей жизни ни разу не занимались машинным обучение, от слова «совсем». Для них область может быть нова, возможно для кого-то само программирование будет вновинку. Какой у вас совет для них?
— Я бы пожелал им оставаться открытыми — к новым идеям, методикам, решениям, позициям. Машинное обучение, на самом деле, проще, чем программирование. В процессе программирования вам необходимо учитывать каждый случай в исходных данных, адаптировать под него логику программы и правила. В это самое время, используя TensorFlow и машинное обучение вы, по сути, тренируете компьютер используя примеры, предоставляя компьютеру самому находить правила.
— Это невероятно интересно! Мне не терпится рассказать студентам этого курса немного больше о машинном обучении! Себастьян, благодарю, что нашел время и пришёл сегодня к нам!
— Благодарю! Оставайтесь на связи!
Что такое машинное обучение?
Итак, давайте начнём со следующей задачи — даны входные и выходные значения.
Когда в качестве входного значения у вас значение 0, то в качестве выходного значения — 32. Когда в качестве входного значения у вас 8, то в качестве выходного значения — 46.4. Когда в качестве входного значения у вас 15, то в качестве выходного значения — 59 и так далее.
Присмотритесь к этим значениям и позвольте мне задать вам вопрос. Можете ли вы определить, каким будет выходное значение, если на входе мы получим 38?
Если вы ответили 100.4, то оказались правы!
Итак, как мы могли решить эту задачу? Если присмотреться внимательнее к значениям, то можно заметить, что они связаны выражением:
Где С — градусы Цельсия (входные значения), F — Фаренгейта (выходные значения).
То, что сейчас сделал ваш мозг — сопоставил входные значения и выходные значения и нашел общую модель (связь, зависимость) между ними, — именно это и делает машинное обучение.
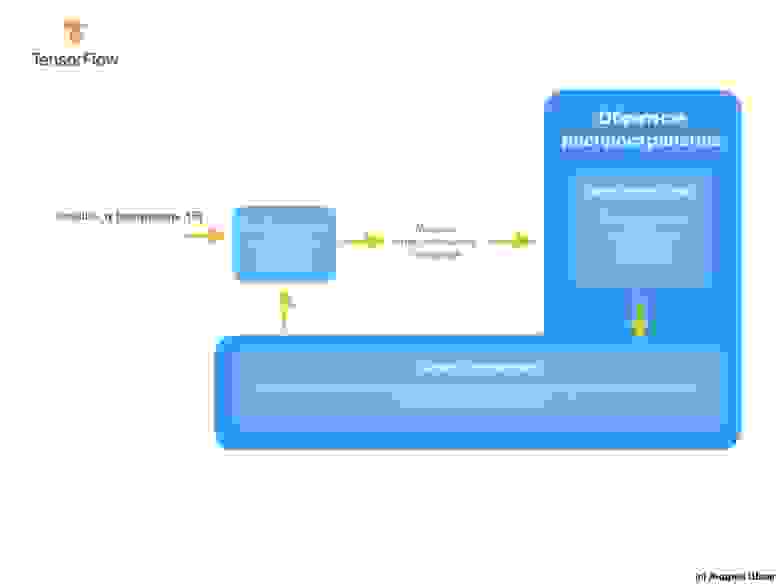
По входным и выходным значениям алгоритмы машинного обучения найдут подходящий алгоритм преобразования входных значений в выходные. Это можно представить следующим образом:
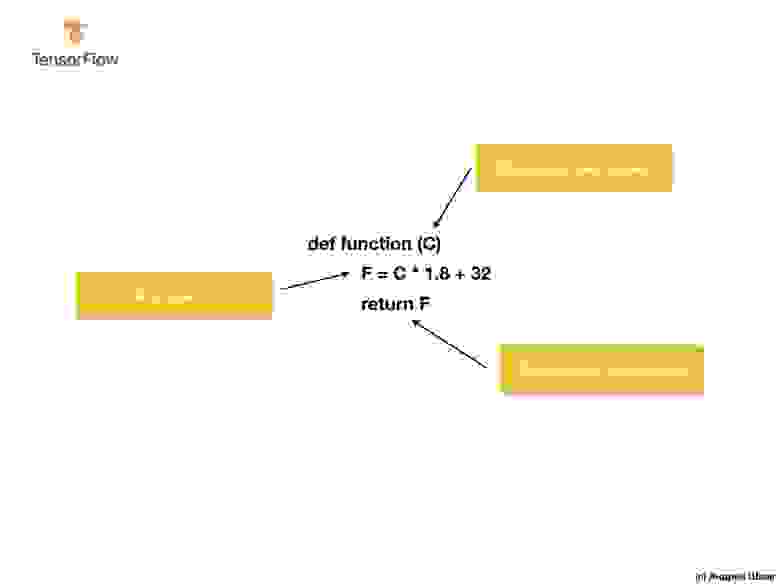
Решение, при подходе с точки зрения традиционной разработки программного обеспечения, может быть реализовано на любом языке программирования с использованием функции:
Итак, что мы имеем? Функция принимает входное значение C, затем вычисляет выходное значение F используя явно заданный алгоритм, а затем возвращает вычисленное значение.
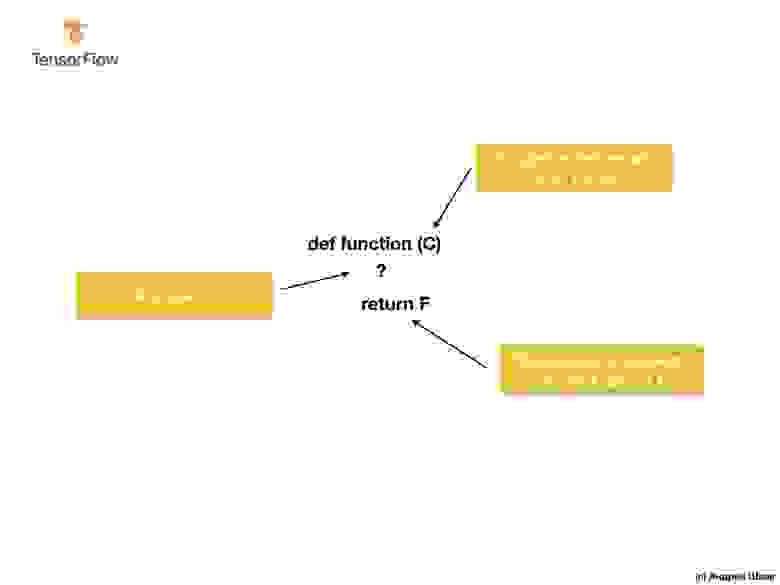
С другой стороны, в подходе с машинным обучением, у нас есть только входные и выходные значения, но не сам алгоритм:
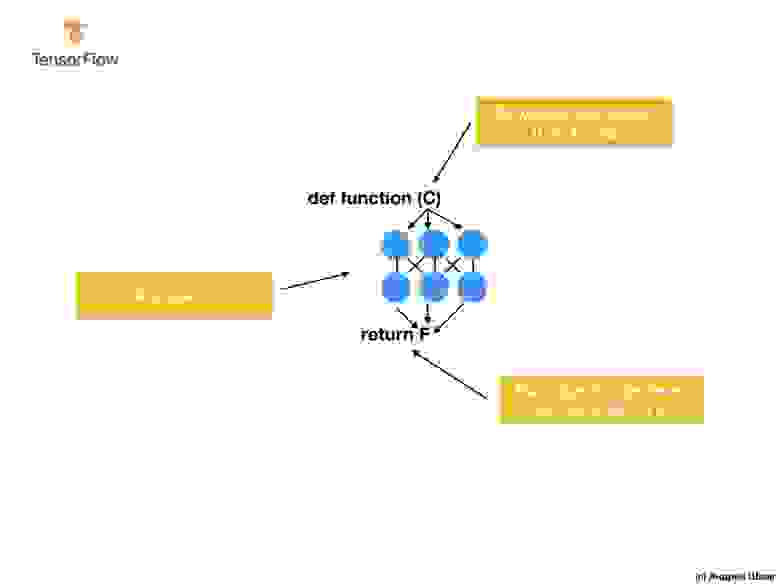
Подход с машинным обучением основывается на использовании нейронных сетей для нахождения отношений между входными и выходными значениями.
Вы можете думать о нейронных сетях, как о стопке слоёв, каждый из которых состоит из заранее известной математики (формул) и внутренних переменных. Входное значение поступает в нейронную сеть и проходит сквозь стопку слоёв нейронов. Во время прохождения через слои, входное значение преобразовывается согласно математике (заданным формулам) и значениям внутренних переменных слоёв, производя выходное значение.
Для того, чтобы нейронная сеть смогла обучиться и определить правильные отношения между входными и выходными значениями, нам необходимо её обучить — натренировать.
Мы тренируем нейронную сеть через повторяющиеся попытки сопоставить входные значения выходным.
В процессе тренировки происходит «подгонка» (подбор) значений внутренних переменных в слоях нейронной сети до тех пор, пока сеть не научится генерировать соответствующие выходные значения соответствующим входным значениям.
Как мы увидим в последующем, для того чтобы обучить нейронную сеть и позволить ей подобрать наиболее подходящие значения внутренних переменных, производят тысячи или десятки тысяч итераций (тренировок).
В качестве упрощенного варианта понимания машинного обучения вы можете представить себе алгоритмы машинного обучения как функции, которые подбирают значения внутренних переменных таким образом, чтобы соответствующим входным значениям соответствовали корректные выходные значения.
Существует множество типов архитектур нейронных сетей. Однако, вне зависимости от того, какую архитектуру вы выберете, математика внутри (какие вычисления выполняются и в каком порядке) останется неизменной в процессе тренировки. Вместо изменения математики, меняются внутренние переменные (веса и смещения) во время тренировки.
Например, в задаче конвертации из градусов Цельсия в Фаренгейты, модель начинает с умножения входного значения на некоторое число (вес) и добавления другого значения (смещения). Обучение модели заключается в нахождении подходящих значений для этих переменных, без изменения выполняемых операций умножения и сложения.
А вот одна крутая вещь над которой стоит задуматься! Если вы решили задачу преобразования градусов Цельсия в Фаренгейты, которая обозначена в видео и в тексте ниже, вы, вероятно, решили её потому, что обладали неким предыдущим опытом или знанием, как производить подобного рода преобразования из градусов Цельсия в Фаренгейты. Например, вы могли просто знать, что 0 градусов Цельсия соответствуют 32 градусам по Фаренгейту. С другой стороны, системы основанные на машинном обучении не обладают предыдущими вспомогательными знаниями для решения поставленной задачи. Они учатся решать подобного рода задачи не основываясь на предыдущих знаниях и при их полном отсутствии.
Довольно разговоров — переходим к практической части лекции!
CoLab: преобразуем градусы Цельсия в градусы Фаренгейта
Основы: обучение первой модели
Добро пожаловать в CoLab, где мы будем тренировать нашу первую модель машинного обучения!
Мы постараемся сохранять простоту преподносимого материала и ввести только базовые понятия необходимые для работы. Последующие CoLabs будут содержать более продвинутые техники.
Задача, которую мы будем решать — преобразование градусов Цельсия в градусы Фаренгейта. Формула преобразования выглядит следующим образом:
Безусловно, было бы проще просто написать функцию конвертации на Python или любом другом языке программирования, которая бы выполняла непосредственные вычисления, но в таком случае это не было бы машинным обучением 🙂
Вместо этого мы подадим на вход TensorFlow имеющиеся у нас входные значения градусов Цельсия (0, 8, 15, 22, 38) и их соответствующие градусы по Фаренгейту (32, 46, 59, 72, 100). Затем мы натренируем модель таким образом, чтобы та примерно соответствовала приведённой выше формуле.
Импорт зависимостей
Подготовка данных для тренировки
Создаём модель
Строим сеть
Мы назовём слой l0 (layer и ноль) и создадим его, инициализировав tf.keras.layers.Dense со следующими параметрами:
Преобразуем слои в модель
Примечание
Достаточно часто вы будете сталкиваться с определением слоёв прямо в функции модели, нежели с их предварительным описанием и последующим использованием:
Компилируем модель с функцией потерь и оптимизаций
Перед тренировкой модель должна быть скомпилирована (собрана). При компиляции для тренировки необходимы:
Функция потерь и функция оптимизации используются во время тренировки модели ( model.fit(. ) упоминаемая ниже) для выполнения первичных вычислений в каждой точке и последующей оптимизации значений.
Действие вычисления текущих потерь и последующее улучшение этих значений в модели — это именно то, чем является тренировка (одна итерация).
Во время тренировки, функция оптимизации используется для подсчета корректировок значений внутренних переменных. Цель — подогнать значения внутренних переменных таким образом в модели (а это, по сути, математическая функция), чтобы те отражали максимально приближённо существующее выражение конвертации градусов Цельсия в градусы Фаренгейта.
TensorFlow использует численный анализ для выполнения подобного рода операций оптимизации и вся эта сложность скрыта от наших глаз, поэтому мы не будем вдаваться в детали в этом курсе.
Что полезно знать об этих параметрах:
Функция потерь (среднеквадратичная ошибка) и функция оптимизации (Adam), используемые в этом примере, являются стандартными для подобных простых моделей, но кроме них доступно множество других. На данном этапе нам не важно каким образом работают эти функции.
Тренируем модель
Во время тренировки модель получает на вход значения градусов Цельсия, выполняет преобразования используя значения внутренних переменных (называемые «весами») и возвращает значения, которые должны соответствовать градусами по Фаренгейту. Так как первоначальные значения весов установлены произвольными, то и результатирующие значения будут далеки от корректных значений. Разница между необходимым результатом и фактическим вычисляется с использованием функции потерь, а функция оптимизации определяет каким образом должны быть подкорректированы веса.
Отображаем статистику тренировок
Используем модель для предсказаний
Теперь у нас есть модель, которая была обучена на входных значениях celsius_q и выходных значениях fahrenheit_a для определения взаимосвязи между ними. Мы можем воспользоваться методом предсказания для вычисления тех значений градусов Фаренгейта по которым ранее нам неизвестны были соответствующие градусы Цельсия.
Например, сколько будет 100.0 градусов Цельсия по Фаренгейту? Попробуйте угадать перед тем как запускать код ниже.
Правильный ответ 100×1.8+32=212, так что наша модель справилась достаточно хорошо!
Смотрим на веса
Значение первой переменной близко к
32. Эти значения (1.8 и 32) являются непосредственными значениями в формуле конвертации градусов Цельсия в градусы Фаренгейта.
Так как представления одинаковые, то и значения внутренних переменных модели должны были сойтись к тем, которые представлены в фактической формуле, что и произошло в итоге.
При наличии дополнительных нейронов, дополнительных входных значений и выходных значений, формула становится немного сложнее, но суть остаётся той же.
Немного экспериментов
Как вы могли уже заметить, текущая модель тоже способна достаточно хорошо предсказывать соответствующие значения градусов Фаренгейта. Однако, если взглянуть на значения внутренних переменных (веса) нейронов по слоям, то никаких значений похожих на 1.8 и 32 мы уже не увидим. Добавленная сложность модели скрывает «простую» форму преобразования градусов Цельсия в градусы Фаренгейта.
Оставайся на связи и в следующей части мы рассмотрим то, каким образом работают Dense-слои «под капотом».
Краткое резюме
Поздравляем! Вы только что обучили свою первую модель. Мы на практике увидели, каким образом по входным и выходным значениям модель научилась умножать входное значение на 1.8 и прибавлять к нему 32 для получения корректного результата.
Это было по-настоящему впечатляюще, учитывая то, сколько строчек кода нам понадобилось написать:
Приведённый выше пример — общий план для всех программ машинного обучения. Вы будете использовать подобные конструкции для создания и обучения нейронных сетей и для решения последующих задач.
Процесс тренировки
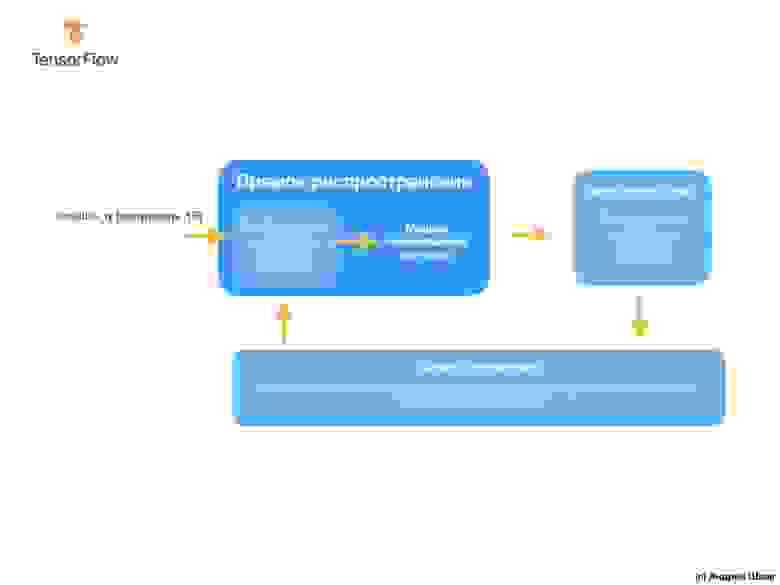
Процесс тренировки (происходящий в методе model.fit(. ) ) состоит из весьма простой последовательности действий, результатом которых должны стать значения внутренних переменных дающих максимально близкий к исходному результаты. Процесс оптимизации, благодаря которому достигаются такие результаты, называется градиентным спуском, использует численный анализ для поиска максимально подходящих значений для внутренних переменных модели.
Чтобы заниматься машинным обучением вам, в принципе, нет необходимости разбираться в этих деталях. Но для тех, кому всё-таки интересно узнать больше: градиентный спуск посредством итераций изменяет значения параметров по-немногу, «вытягивая» их в нужном направлении, до тех пор пока не будут получены наилучшие результаты. В данном случае «лучшие результаты» (лучшие значения) означают, что любое последующее изменение параметра только ухудшит результат модели. Функция, которая измеряет насколько хороша или плоха модель на каждой итерации называется «функцией потерь», и цель каждого «вытягивания» (корректировки внутренних значений) — уменьшить значение функции потерь.
Процесс тренировки начинается с блока «прямое распространение», при котором входные параметры поступают на вход нейронной сети, следуют к скрытым нейронам и затем идут к выходным. Затем модель применяет внутренние преобразования над входными значениями и внутренними переменными для предсказания ответа.
В нашем примере, входным значением является температура в градусах Цельсия и модель предсказывала соответствующее значение в градусах Фаренгейта.
После вычисления значения потери, внутренние переменные (веса и смещения) всех слоёв нейронной сети подвергаются корректировке для минимизации значения потери с целью приближения выходного значения к корректному исходному эталонному значению.
Для этого курса не является обязательным понимание принципов работы процесса тренировки, однако, если вы достаточно любопытны, то можете найти больше информации в Google Crash Course (перевод и практическая часть всего курса заложены у автора в планах к публикации).
К этому моменты вы уже должны быть знакомы со следующими терминами:
Dense-слои
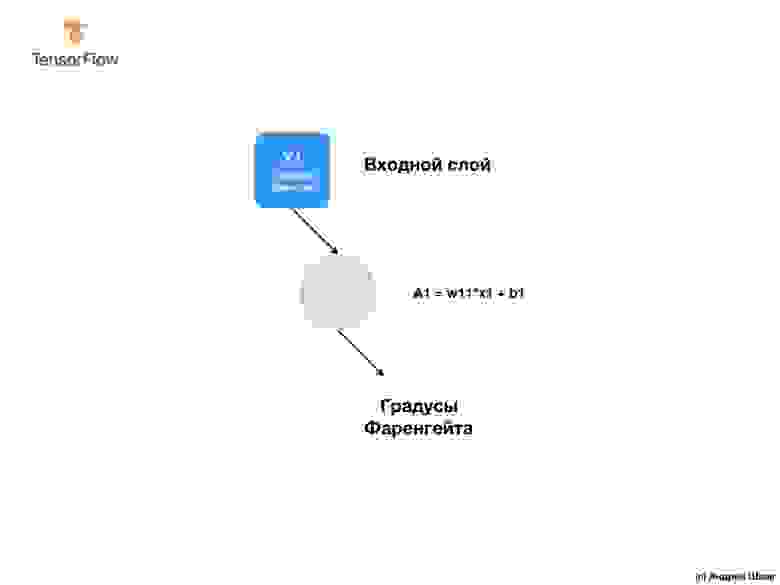
В предыдущей части мы создали модель, которая конвертирует градусы Цельсия в градусы Фаренгейта, используя простую нейронную сеть для нахождения зависимости между градусами Цельсия и градусами Фаренгейта.
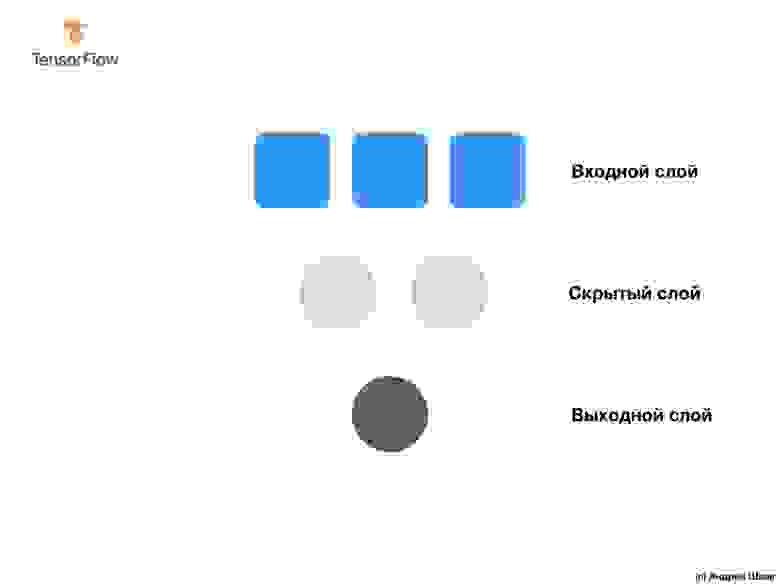
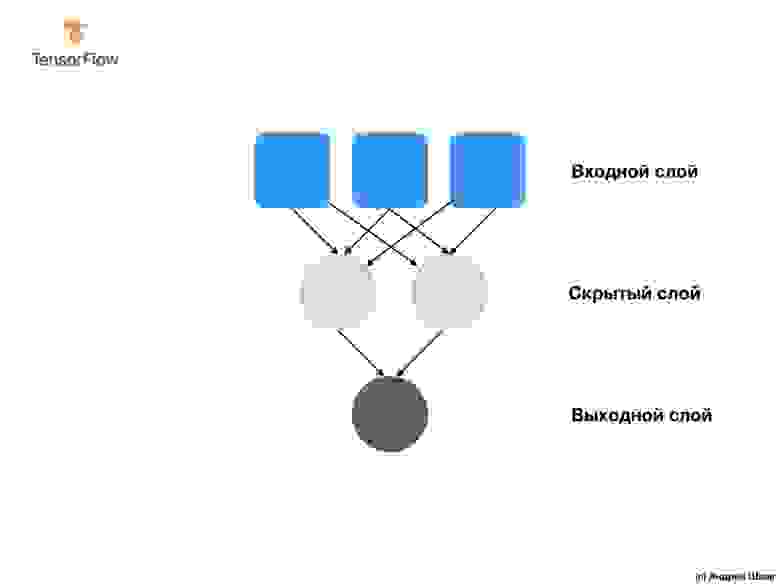
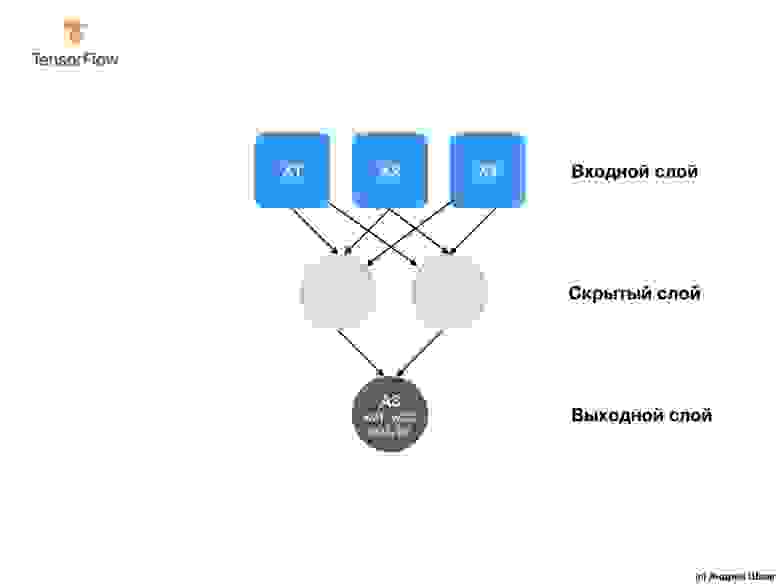
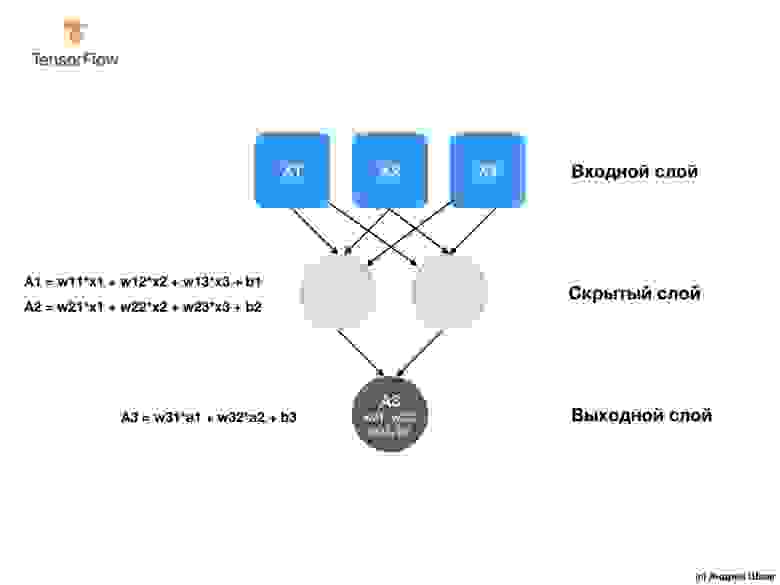
Наша сеть состоит из единственного полносвязного слоя. Но что такое полносвязный слой? Чтобы в этом разобраться давайте создадим более сложную нейронную сеть у которой 3 входных параметра, один скрытый слой с двумя нейронами и один выходной слой с единственным нейроном.
Чтобы создать приведенную выше нейронную сеть нам достаточно следующих выражений:
Итак, мы разобрались с тем, что такое нейроны и как они связаны между собой. Но как на самом деле работают полносвязные слои?
Чтобы понять, что же на самом деле там происходит и что они делают, нам понадобится заглянуть «под капот» и разобрать внутреннюю математику нейронов.
Что обязательно стоит иметь ввиду — внутренняя математика нейрона остаётся неизменной. Другими словами, в процессе тренировки меняются только веса и смещения.
Когда начинаешь изучать машинное обучение это может показаться странным — тот факт, что это действительно работает, но именно так работает машинное обучение!
Давайте теперь вернёмся к нашему примеру конвертации градусов Цельсия в градусы Фаренгейта.
Если мы вернёмся к результатам работы нашей модели из практической части, то обратим внимание на то, что показатели веса и смещения были «откалиброваны» таким образом, что примерно соответствуют значениям из формулы.
Мы целенаправленно создали именно такой практический пример, чтобы наглядно показать точное сопоставление между весами и смещениями. Применяя машинное обучение на практике, мы никогда не сможем подобным образом сопоставить значения переменных с целевым алгоритмом, как в приведённом выше примере. Как мы сможем это сделать? Никак, потому что мы даже не знаем целевого алгоритма!
Решая задачи машинного обучения мы тестируем различные архитектуры нейронных сетей с различным количеством нейронов в них — методом проб и ошибок находим наиболее точные архитектуры и модели и надеемся, что они решат поставленную задачу в процессе обучения. В следующей практической части мы сможем изучить конкретные примеры такого подхода.
Оставайтесь на связи, потому что сейчас начнётся самое интересное!
Итоги
… и стандартные call-to-action — подписывайся, ставь плюс и делай share 🙂