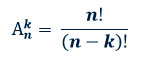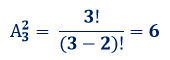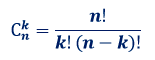Что называют числом перестановок без повторений запишите формулу
Рассмотрим сначала некоторые общие термины.
Размещения без повторений.
Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.
Обратим внимание на следующие важные положения:
Формула для определения числа размещений без повторений:
Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?
Действительно, комбинаций, удовлетворяющих условию, всего шесть:
Перестановки без повторений.
Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n ), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.
Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.
Формула для определения числа перестановок без повторений
Pn = n! = n * (n − 1) * (n − 2) *. * 2 * 1
Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?
Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
Pn = 3! = 3 * 2 * 1 = 6
Сочетания без повторений.
Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.
Формула для определения числа сочетаний без повторений:
Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?
Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.
Воспользуемся формулой для расчета числа различных сочетаний без повторений:
Copyright © 2014-2021, Урок информатики
Все права защищены