Что называют алгебраической дробью

Понятие алгебраической дроби. Основное свойство

Определение алгебраической дроби

Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).

Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).

Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.

Алгебраические (рациональные) дроби

Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.

Основное свойство алгебраической дроби

При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:

Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:

Приведение алгебраических дробей к общему знаменателю

Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:

Алгоритм приведения алгебраических дробей к общему знаменателю

Шаг 2. Дополнительные множители

Перемена знака у члена дроби

Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:

Дробь также не изменится, если провести следующие перемены знаков:

Ещё несколько полезных формул, связанных с переменой знаков:

Примеры

Пример 1. Найдите допустимые значения переменных, входящих в дробь:

$ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$

$ 3x-1 \neq 0 \iff x \neq \frac<1><3>$

$$ x- \frac<4> \neq 0 \iff \frac \neq 0 \iff <\left\< \begin x^2-4 \neq 0 \\ x \neq 0 \end \right.> \iff x \neq <0; \pm2>$$

$ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff <\left\< \begin |y| \neq 0 \\ |y| \neq 3 \end \right.> \iff y \neq <0; \pm3>$

Пример 2. Сократите дроби:

Пример 3. Упростите выражение:

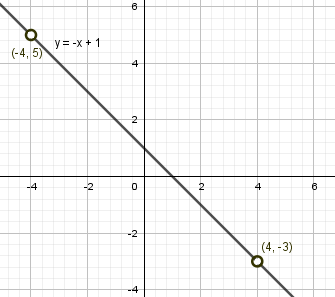
Пример 4. Постройте график функции:

(О графике линейной функции – см. §38 справочника для 7 класса)

Источник

Основное свойство алгебраических дробей

Определение алгебраической дроби

В §1 данного справочника мы уже давали определение алгебраических выражений, как целых, так и дробных. А в §14 данного справочника мы ввели понятие многочлена.

Алгебраическая дробь – это дробь, в которой числитель и знаменатель – многочлены (при условии, что знаменатель отличен от нуля).

Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.

При этом b может быть любым действительным числом, без ограничений.

Основное свойство алгебраической дроби

При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:

Это свойство означает, что мы может сокращать алгебраическую дробь на общий множитель, если такой найдётся для числителя и знаменателя. Например:

Также, это свойство разрешает нам приводить алгебраические дроби к общему знаменателю и выполнять сложение или вычитание. Например:

Примеры

Пример 1. Найдите допустимые значения переменных, входящих в дробь:

Пример 2. Выразите переменные из формул:

а) s = vt. Найти v и t

б)m = ρV. Найти ρ и V

в) p = ρgh. Найти ρ и h

$$vt = x-x_0 \Rightarrow v = \frac, t = \frac$$

Пример 3. Сократите дроби:

Пример 4. Разложите на множители числитель и знаменатель и сократите дроби:

Источник

Алгебраическая дробь — это дробь, числитель и знаменатель которой —многочлены(причем знаменатель отличен от нуля).

Введение

В этом реферате я бы хотела рассказать об алгебраических дробях. Что же это такое? Кто «открыл» эти дроби? Какова история их происхождения? Как их примененяют? Постараюсь ответить на поставленные мною вопросы и как можно больше заинтересовать читателя/слушателя.

Цель исследования: узнать, что такое алгебраическая дробь, исследовать свойства алгебраических дробей, углубиться в их историю.

— познакомиться с предметом исследования

-усовершенствовать свои знания

Из истории возникновения обыкновенных дробей.

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.

В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.

Первым европейским учёным который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник, сын городского писаря Фиббоначи (Леонардо Пизанский).

В 1202 году он ввёл слово «дробь».

Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик.

Дроби на Руси

В русском языке слово «дробь» появилось лишь в VIII веке. Происходит слово «дробь» от слова «дробить, разбивать, ломать на части». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять». В первых учебниках дроби назывались «ломанные числа». В старых руководствах находили следующие названия дробей на Руси:

– половина, полтина, – треть,

– полполчеть, – полполполтреть (малая треть),

– полполполчеть (малая четь), – пятина,

4.Что такое алгебраическая дробь?

Алгебраическая дробь — это дробь, числитель и знаменатель которой —многочлены(причем знаменатель отличен от нуля).

Другое название таких дробей — рациональные.

Поскольку одночлен считают многочленом, состоящим из одного члена, в числителе и знаменателе алгебраических (рациональных) дробей могут стоять одночлены ( в том числе, числа).

Примеры алгебраических (рациональных) дробей:

Источник

Что называют алгебраической дробью

В § 42 было сказано, что если деление многочленов нельзя выполнить нацело, то частное записывается в виде дробного выражения, в котором делимое является числителем, а делитель — знаменателем.

Примеры дробных выражений:

Числитель и знаменатель дробного выражения и сами могут быть дробными выражениями, например:

Из дробных алгебраических выражений наиболее часто приходится иметь дело с такими, в которых числитель и знаменатель являются многочленами (в частности, и одночленами). Каждое такое выражение называется алгебраической дробью.

Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой — многочлены, называется алгебраической дробью.

Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.

В дальнейшем, изучив действия над алгебраическими дробями, мы сможем всякое дробное выражение при помощи тождественных преобразований преобразовать в алгебраическую дробь.

Примеры алгебраических дробей:

Заметим, что целое выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать в числителе данное выражение, а в знаменателе 1. Например:

2. Допустимые значения букв.

Буквы, входящие только в числитель, могут принимать любые значения (если не введены какие-либо дополнительные ограничения условием задачи).

Для букв же, входящих в знаменатель, допустимыми являются только те значения, которые не обращают в нуль знаменатель. Поэтому в дальнейшем всегда будем считать, что знаменатель алгебраической дроби не равен нулю.

3. Значение дроби.

Надо различать алгебраическую дробь от ее значения. Значение алгебраической дроби может быть как целым, так и дробным числом, положительным, отрицательным, нулём. Например, значение дроби

Источник

Конспект «Понятие алгебраической дроби»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Урок 1
Тема: Понятие алгебраической дроби.

Цели : ввести понятие алгебраической дроби, формировать умение составлять алгебраические дроби и искать их значения при заданных значениях переменных.

I этап. Организационный момент.

II этап. Устная работа.

– Назовите дробь по данному частному:

III этап. Объяснение нового материала.

После введения данного определения дать учащимся задание на распознание алгебраических дробей.

Задание: Определите, какие из данных выражений являются алгебраическими дробями. Ответ объясните.

а) ; г) ;

б) ; д) ax – 2;

в) ; е) .

IV этап. Формирование умений и навыков.

Все задания, выполняемые учащимися на этом уроке, можно условно разбить на три группы.

1. Использование понятия алгебраической дроби при ее записи.

2. Нахождение значений дроби при заданных значениях переменных.

3. Составление алгебраических дробей по каким-либо условиям.

№ 2 (а, в). – Выполнение данного упражнения целесообразно начать с числовых примеров: 48 : 4 = 12, поскольку 4 · 12 = 48. Это даст учащимся возможность осознанно подойти к выполнению задания.

№ 3 (а, в, д). При выполнении каждого задания можно вызвать к доске сразу нескольких учащихся. У каждого из них получатся разные выражения. После нахождения этих выражений сделать ряд выводов:

– в качестве искомого выражения можно взять произведение данных выражений;

– выражений, удовлетворяющих условию задания, бесконечно много.

№ 4 (а, в), № 6 (а, г), № 12 (а, г). При вычислении необходимо следить за грамотной записью учащихся на доске и у себя в тетрадях. В № 12 выражение сначала нужно упростить.

г)

при с = –1 и d = 11 .

№ 15 (а). В случае затруднения учащихся при выполнении данного задания нужно напомнить им, что для выражения переменной из формулы достаточно рассматривать эту переменную или выражение, в которое она входит как неизвестный множитель (слагаемое, делитель и т. д.).

V этап. Итоги урока.

– Какая дробь называется алгебраической?

– Можно ли многочлен представить в виде алгебраической дроби? Как это сделать?

– Как находится значение алгебраической дроби при заданных значениях переменных?

– Как выражаются различные переменные из формул?

Сегодня на уроке я узнал….

Мне испытывал затруднения….

Я могу себя похвалить за….

Домашнее задание: Выполните любые 5 заданий из упражнений, которые мы решали в классе, и № 12(в) *

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник