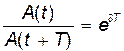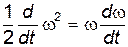Что называется затухающим колебанием
Характеристика затухающих колебаний, какие колебания называют затухающими
Содержание:
В реальной колебательной системе колебания не будут строго периодическими. С каждым циклом их амплитуда падает вследствие действия сторонних сил, например, трения. Со временем автоколебания затухают. Рассмотрим, какие механические колебания называются затухающими, какими свойствами обладают. Наведём примеры таких явлений в природе, быту, промышленности.
Определение и характеристики затухающих колебаний
Часть внутренней энергии системы, которая не восполняется, уходит на преодоление сопротивления, не компенсируется, и вскоре её энергетический запас падает до ноля. Затраты имеют различный характер, зависящий от условий: преодоление сопротивления воздуха (жидкости) качающимся на пружине грузом, трение шариков в подшипнике о внутреннее и внешнее кольца.
Кроме того, энергетический запас частично расходуется на передачу движения окружающей среде – груз или колеблющийся на нитке шар заставляют молекулы окружающего воздуха перемещаться.
Деформация вибрирующей пластины, пружины, растягивание нитки отбирает у контура часть внутренней энергии из-за трения в них самих.
Свободные незатухающие колебания или собственные характерны для идеальной системы, где отсутствует трение. Они актуальны для упрощения решения практических задач:
Незатухающие колебания превращается в затухающие, когда возникает потеря энергии.
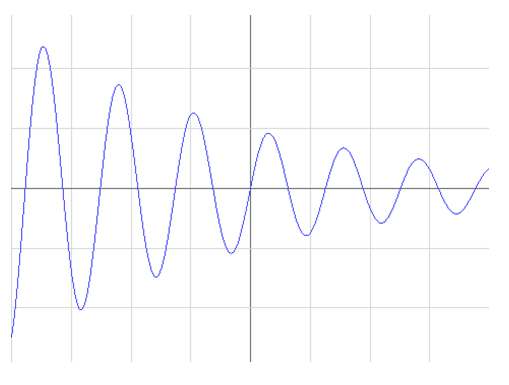
График затухающих колебаний выглядит следующим образом. Амплитуда и частота (значит и периодичность) синусоиды снижаются.
При незатухающих характеристики остаются постоянными.
Примеры затухающих колебаний
Затухающие колебания встречаются в природе и быту:
Наведите собственные примеры описанных явлений, встречаемых в жизни.
Затухающие колебания
Определение и причины затухания колебаний
Причина затухания заключается в том, что во всякой колебательной системе, кроме возвращающей силы, всегда действуют разного рода силы трения, сопротивление воздуха
и т. п., которые тормозят движение. При каждом размахе часть полной колебательной энергии (потенциальной и кинетической) расходуется на работу против сил трения. В конечном итоге на эту работу уходит весь запас энергии, сообщенный колебательной системе первоначально.
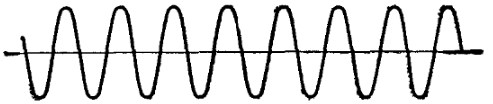
Рассматривая свободные гармонические колебания, мы имели дело с идеальными, строго периодическими собственными колебаниями. Описывая при помощи такой модели реальные колебания, мы сознательно допускаем неточность в описании. Однако подобное упрощение является пригодным в силу того, что у многих колебательных систем затухания колебаний, вызванные трением, действительно малы: система успевает совершить много колебаний прежде, чем их амплитуда уменьшится заметным образом.
Графики затухающих колебаний
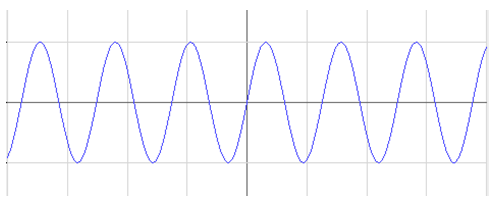
При наличии затухания собственное колебание (рис.1) перестает быть гармоническим. Более того, затухающее колебание перестает быть периодическим процессом — трение влияет не только на амплитуду колебаний (то есть является причиной затухания), но и на продолжительность размахов. С увеличением трения время, необходимое системе для совершения одного полного колебания, увеличивается. График затухающих колебаний представлен на рис. 2.
Рис.1. График свободных гармонических колебаний
Рис.2. График затухающих колебаний
Характерной чертой колебательных систем является то, что небольшое трение влияет на период колебаний в гораздо меньшей степени, чем на амплитуду. Это обстоятельство сыграло огромную роль в усовершенствовании часов. Первые часы с маятником построил голландский физик и математик Христиан Гюйгенс в 1673 г. Этот год можно считать датой рождения современных часовых механизмов. Ход часов с маятником мало чувствителен к изменениям, обусловленным трением, которые в общем случае зависят от многих факторов, в то время как скорость хода предшествующих безмаятниковых часов очень сильно зависела от трения.
На практике возникает потребность как в уменьшении, так и в увеличении затухания колебаний. К примеру, при конструировании часовых механизмов стремятся уменьшить затухание колебаний балансира часов. Для этого ось балансира снабжают острыми наконечниками, которые упираются в хорошо отполированные конические подпятники, выполненные из твердого камня (агата или рубина). Наоборот, во многих измерительных приборах очень желательно, чтобы подвижная часть устройства устанавливалась в процессе измерений быстро, но совершая большого числа колебаний. Для увеличения затухания в этом случае применяют различные демпферы – устройства, увеличивающие трение и, в общем случае, потерю энергии.
СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ



ОБЩИЕ СВЕДЕНИЯ
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса.
Дифференциальное уравнение гармонических колебаний имеет вид:
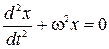
где 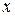
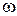
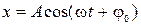
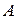
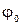
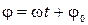
Амплитуда – максимальное значение колеблющейся величины.
Период колебаний – промежуток времени, через который происходит повторение движения тела. Фаза колебания за период получает приращение 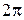
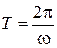
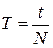
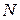
Частота колебаний – число полных колебаний, совершаемых в единицу времени. 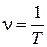
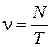
Циклическая частота – число колебаний, совершаемых за 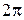
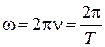
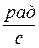
Фаза колебаний – величина, стоящая под знаком косинуса и характеризующая состояние колебательной системы в любой момент времени.
Начальная фаза – фаза колебаний в начальный момент времени. Фаза и начальная фаза измеряются в радианах ( 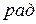
Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.
Дифференциальное уравнение свободных затухающих колебаний имеет вид:
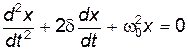
| где x – | колеблющаяся величина, описывающая тот или иной физический процесс; |
| d – | коэффициент затухания; |
| w0 – | циклическая частота собственных незатухающих колебаний (собственная частота колебательной системы). |
Решение уравнения (1) в случае малого затухания (d 2
Тогда период затухающих колебаний вычисляют по формуле:
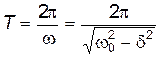
Если A(t) и A(t + T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм:
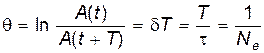
Величина Ne – это число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная величина для данной колебательной системы.
Для характеристики колебательной системы используют понятие добротности Q, которая при малых значениях логарифмического декремента равна
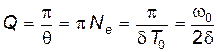
Добротность пропорциональна числу колебаний, совершаемых системой за время релаксации.
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ С ПОМОЩЬЮ НАКЛОННОГО МАЯТНИКА
Теоретическое обоснование методики определения коэффициентатрения
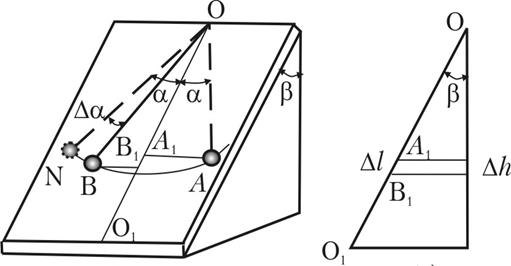
Наклонный маятник представляет собой шар, подвешенный на длинной нити и лежащий на наклонной плоскости.
Если шар отвести из положения равновесия (ось OO1) на угол a, а затем отпустить, то возникнут колебания маятника. При этом шар будет кататься по наклонной плоскости около положения равновесия (рис. 1, а). Между шаром и наклонной плоскостью будет действовать сила трения качения. В результате колебания маятника будут постепенно затухать, то есть будет наблюдаться уменьшение во времени амплитуды колебаний.
Можно предположить, что по величине затухания колебаний могут быть определены сила трения и коэффициент трения качения.
Выведем формулу, которая связывает уменьшение амплитуды колебаний с коэффициентом трения качения m.При качении шара по плоскости сила трения совершает работу. Эта работа уменьшает полную энергию шара. Полная энергия складывается из кинетической и потенциальной энергий. В тех положениях, где маятник максимально отклонен от положения равновесия, его скорость, а следовательно, и кинетическая энергия равны нулю.
Эти точки называются точками поворота. В них маятник останавливается, поворачивается и движется обратно. В момент поворота энергия маятника равна потенциальной энергии, поэтому уменьшение потенциальной энергии маятника при его движении от одной точки поворота до другой равна работе силы трения на пути между точками поворота.
Пусть А – точка поворота (рис. 1, а). В этом положении нить маятника составляет угол a с осью OO1.Если бы трения не было, то через половину периода маятник оказался бы в точке N, а угол отклонения был бы равен a. Но из-за трения шар немного не докатится до точки N и остановится в точке В.Это и будет новая точка поворота. В этой точке угол нити с осью OO1будет равен 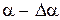
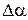
Найдем связь между потерей угла 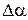
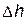
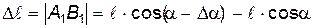
где 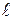
Так как ось OO1 наклонена под углом 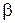
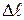
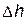
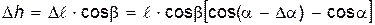
При этом изменение потенциальной энергии маятника при переходе его из положения A в положение В равно:
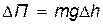
g – ускорение свободного падения.
Вычислим работу силы трения.
Сила трения определяется по формуле:
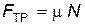
| где m – | коэффициент трения; |
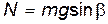 – – | сила нормальной реакции плоскости. |
Путь 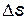
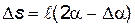
Работа силы трения на пути 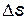
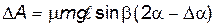
Но 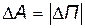
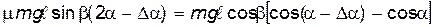
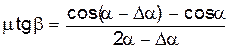
Таким образом, формула (6) приобретает вид:
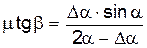
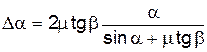

С другой стороны, пусть угол a будет малым настолько, чтобы можно было считать, что 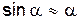
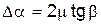
Формула (8) справедлива, если:
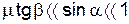
Итак, за время одного полного колебания потеря угла составит:
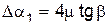
а за n колебаний – 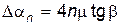
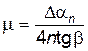
Формула (10) дает удобный способ определения коэффициента трения качения. Необходимо измерить уменьшение угла Dan за 10-15 колебаний, а затем по формуле (10) вычислить m.
В формуле (10) величина Da выражена в радианах. Чтобы использовать значения Da в градусах, формулу (10) необходимо видоизменить:
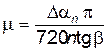
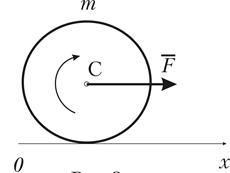
Выясним физический смысл коэффициента трения качения. Рассмотрим сначала более общую задачу. Шар массой m и моментом инерции Ic относительно оси, проходящей через центр масс, движется по гладкой поверхности (рис. 2).
Рис. 2 
К центру масс C приложена сила 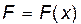
Уравнения движения шара в этом случае имеют вид:
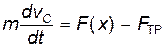
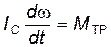
где 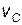
w – угловая скорость.
В уравнениях (12) и (13) четыре неизвестных: 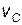
Допустим, что:
1) тело катится без проскальзывания. Тогда:
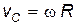
где R – радиус шара;
2) тело и плоскость являются абсолютно жесткими, т.е. тело не деформируется, а касается плоскости в одной точке О (точечный контакт), тогда между моментом силы трения и силой трения имеется связь:
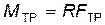
С учетом формул (14) и (15) из уравнений (12) и (13) получаем выражение для силы трения:
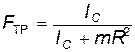
Выражение (16) не содержит коэффициента трения m, который определяется физическими свойствами соприкасающихся поверхностей шара и плоскости, такими, как шероховатость, или вид материалов, из которых изготовлены шар и плоскость. Этот результат – прямое следствие принятой идеализации, отражаемой связями (14) и (15). Кроме того, легко показать, что в принятой модели сила трения не совершает работы. Действительно, умножим уравнение (12) на 
и складывая выражения (12) и (13), получаем
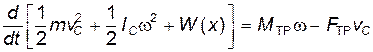
где W(x) – потенциальная энергия шара в поле силы F(x). Следует учесть, что
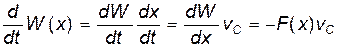
Очевидно, что и этот несколько странный результат также следствие принятой идеализации. Это свидетельствует о том, что принятая идеализация не отвечает физической реальности. В самом деле, в процессе движении шар взаимодействует с плоскостью, поэтому его механическая энергия должна убывать, а это значит, что связи (14) и (15) могут быть верны лишь настолько, насколько можно пренебречь диссипацией энергии.
Совершенно ясно, что в данном случае нельзя принять такую идеализацию, поскольку наша цель – определить по изменению энергии маятника коэффициент трения. Поэтому будем считать справедливым предположение об абсолютной жесткости шара и поверхности, а значит, и справедливой связи (15). Однако откажемся от предположения, что шар движется без проскальзывания. Мы допустим, что имеет место слабое проскальзывание.
Пусть скорость точек касания (на рис. 2 точка О) шара (скорость проскальзывания):
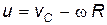
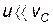
Тогда, подставляя в уравнение (17) 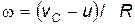
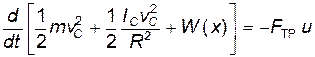
из которого видно, что скорость диссипации энергии равна мощности силы трения. Результат вполне естественный, т.к. тело скользит по поверхности со скоростью и, нанего действует сила трения, совершающая работу, вследствие чего полная энергия системы уменьшается.
Выполняя в уравнении (21) дифференцирование и учитывая соотношение (18), получаем уравнение движения центра масс шара:
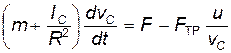
Оно аналогично уравнению движения материальной точки массой:
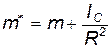
под действием внешней силы F и силы трения качения:
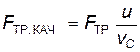
Причем, FТР – обычная сила трения скольжения. Следовательно, при качении шара эффективная сила трения, которую называют силой трения качения, есть просто обычная сила трения скольжения, умноженная на отношение скорости проскальзывания к скорости центра масс тела. На практике часто наблюдается случай, когда сила трения качения не зависит от скорости тела.
Видимо, в этом случае скорость проскальзывания и пропорциональна скорости тела:
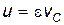
где e – коэффициент пропорциональности. Обычно 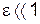
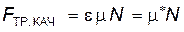
где m * – коэффициент трения качения. Естественно, независимость силы трения качения от скорости тела может быть проверена только опытным путем. Если это так, то уравнение движения шара (22) имеет вид:
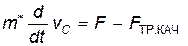
здесь FТР.КАЧ – постоянная величина.
Точно такое же уравнение можно получить, если оставить связь (14), но вместо условия (15) использовать формулу связи между моментом силы трения и силой трения: